Chapter 2 Vocab Angles Vers

Honors Geo

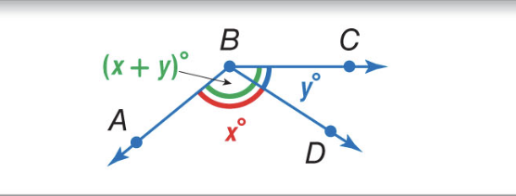
Angle Addition Postulate

D is the interior of ∠ABC if and only if m∠ABD+ m∠DBC = m∠ABC

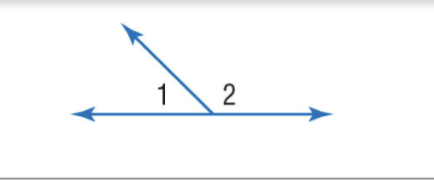
Supplement Theorem

If two angles form a linear pair, then they are supplementary angles. Ex. m∠1 + m∠2 = 180

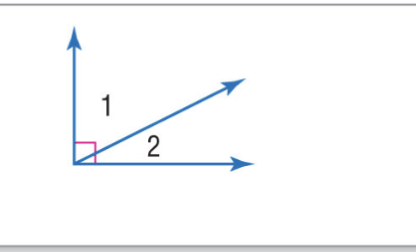
Complement Theorem

If the noncommon sides of two adjacent angles form a right angle, then the angles are complementary angles. Ex. m∠1 + m∠2 = 90

Congruent Supplements Theorem

Angles supplementary to the same angle or to congruent angles are congruent. EX. If m∠1 + m∠2 = 180 and m∠2 + m∠3 = 180 then ∠1 ≅ ∠3

Congruent Complement Theorem

Angles complementary to the same angle or to congruent angles are congruent. Ex. If m∠4 +m∠5 = 90 and m∠5 + m∠6 = 90 then ∠4 ≅∠6

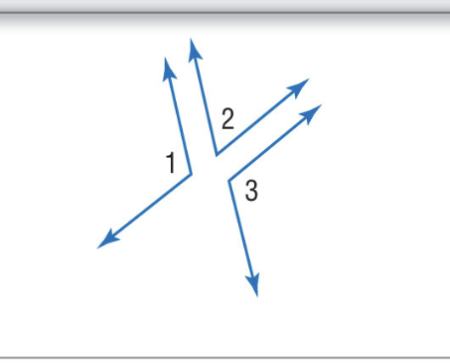
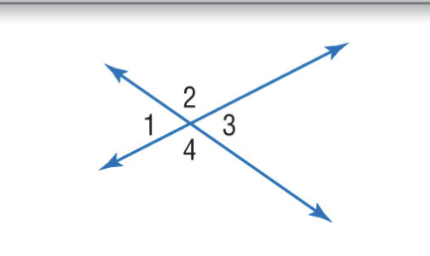
Vertical Angles Theorem 

If two angles are vertical angles, then they are congruent. Ex ∠1≅∠3 and ∠2 ≅∠4

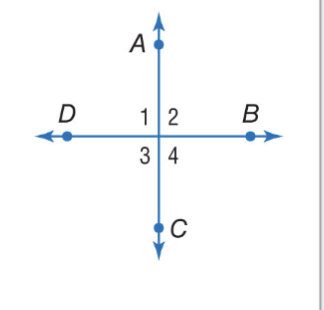
Right Angle Theorems (Perpendicular) 

Perpendicular Lines intersect to form four right angles. Ex. If AC ⟂ DB, then ∠1, ∠2, ∠3, and ∠4 are right angles.

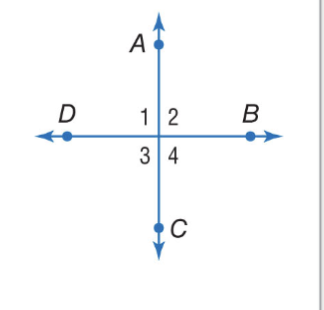
Right Angle Theorem ( Congruence)

All right angles are congruent. Ex. If ∠1, ∠2, ∠3, and ∠4 are right angles, then
∠1 ≅ ∠2 ≅ ∠3 ≅ ∠4.

Right Angle Theorems (Perpendicular) 

Perpendicular lines form congruent adjacent angles. Ex. If AC ⟂ DB, then
∠1 ≅ ∠2, ∠2 ≅ ∠4, ∠3 ≅ ∠4, and ∠1 ≅ ∠3.

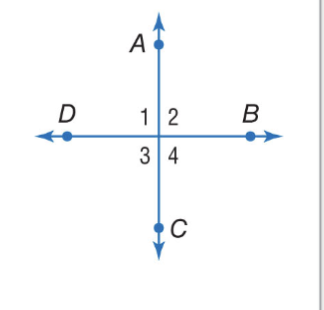
Right Angle Theorems ( congruent and supplementary)

If two angles are congruent and supplementary, then each angle is a right angle. Ex. f ∠5 ≅ ∠6 and ∠5 is supplementary to ∠6,
then ∠5 and ∠6 are right angles.

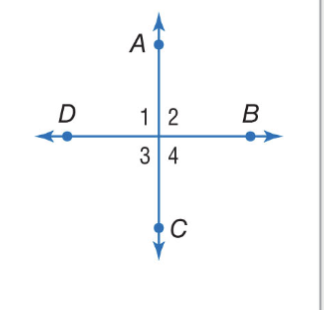
Right Angle Theorems ( Linear Pair)

If two congruent angles form a linear pair, then they are right angles. Ex. If ∠7 and ∠8 form a linear pair,
then ∠7 and ∠8 are right angles.

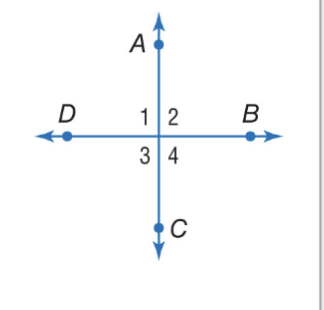
Reflexive Property of Congruence 

∠1≅∠1

Symmetric Property of Congruence

If ∠1 ≅∠2 then ∠2≅∠1

Transitive Property of Congruence

If ∠1 ≅∠2 and ∠2≅∠3 then ∠1 ≅∠3