Charged Particles, Conductors and Electric and Magnetic Fields

How are electric fields defined and represented

defined by the direction of fore on a positive text charge

• Electric field lines come out at 90° to the surface of the charge

• Denser the lines = stronger the field

• For a point charge, it is when it is closer to the charge

• More lines = more charge (e.g. double the lines = double the charge)

  

Note: MASS does not contribute to electric field strength, only magnitude of CHARGE

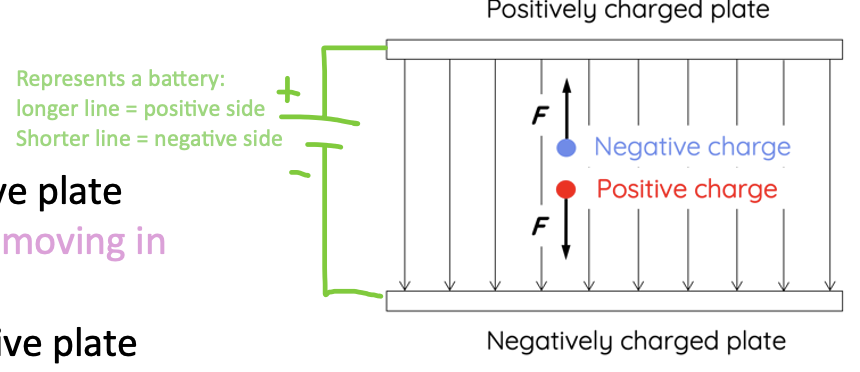
Uniform electric field

created by parallel plates

• Same electric field strength at any point

• Direction of E field is in the same direction

• Negative charge = moves against field towards positive plate

  • negative sign (if you put charge as negative) = it is moving in opposite direction to field lines

• Positive charge = moves with the field towards negative plate

Equation for electric field strength + force in constant e field

q = number of electrons x charge of electrons (-1.602×10^-19)

F=qE → lorenz force

E=V/d = F/q

Note: Force between charged objects

Charged object → makes electric field → electric force → work → change in energy (K or U)

Coulombs law

force between two-point charges

Potential difference and work

Potential difference (voltage)

work done per unit charge moving between two points

V=W/q

Work (change in K or U energy)

W=∆K=qEd=qV

Motion of charges in electric fields

• Milikan oil drop

• 1D

• 2D

Millikan’s Oil drop experiment	When a charge is suspended motionless between two plates ∴ Fnet = 0 ∴ Electric force = gravitational force ∴ qE = ma  can put values in and rearrange for unknowns To find the charge of the particle: Figure out the charges of the plates Draw electric field lines Draw a free body diagram Gravitational force will always be downwards The electric force will be the force opposing the g force Force is parallel to field lines = positive Force is opposing field lines = negative
1D	When a charge attracted to the plate of the opposite charge (only x or y direction) either placed at rest of accelerated towards that plate it will accelerate towards that plate (only up or down/ left or right) (What was studied above)
2d	When a charge is moving in the x and y direction Find the net force acting on the particle: F = qE = ma Rearrange for a: a=qE/m Describe the motion of the particle Horizontal motion: constant velocity, no acceleration Vertical motion: constant acceleration Positive = accelerate in the same direction of electric field Negative = accelerate in the opposite direction of electric field Decompose the initial velocity into x and y components Can use SUVAT equations to solve for unknowns → but use acceleration in (2) Y: v = u + at / s = ut + ½at2 / v2 = u2 +2as Vertical deflection is the distance it travelled vertically Angle of deflection → usually means at the end of the motion (use tan inverse and the decomposed velocities) X: S = Ut / v = u
Radial field	coulomb’s law

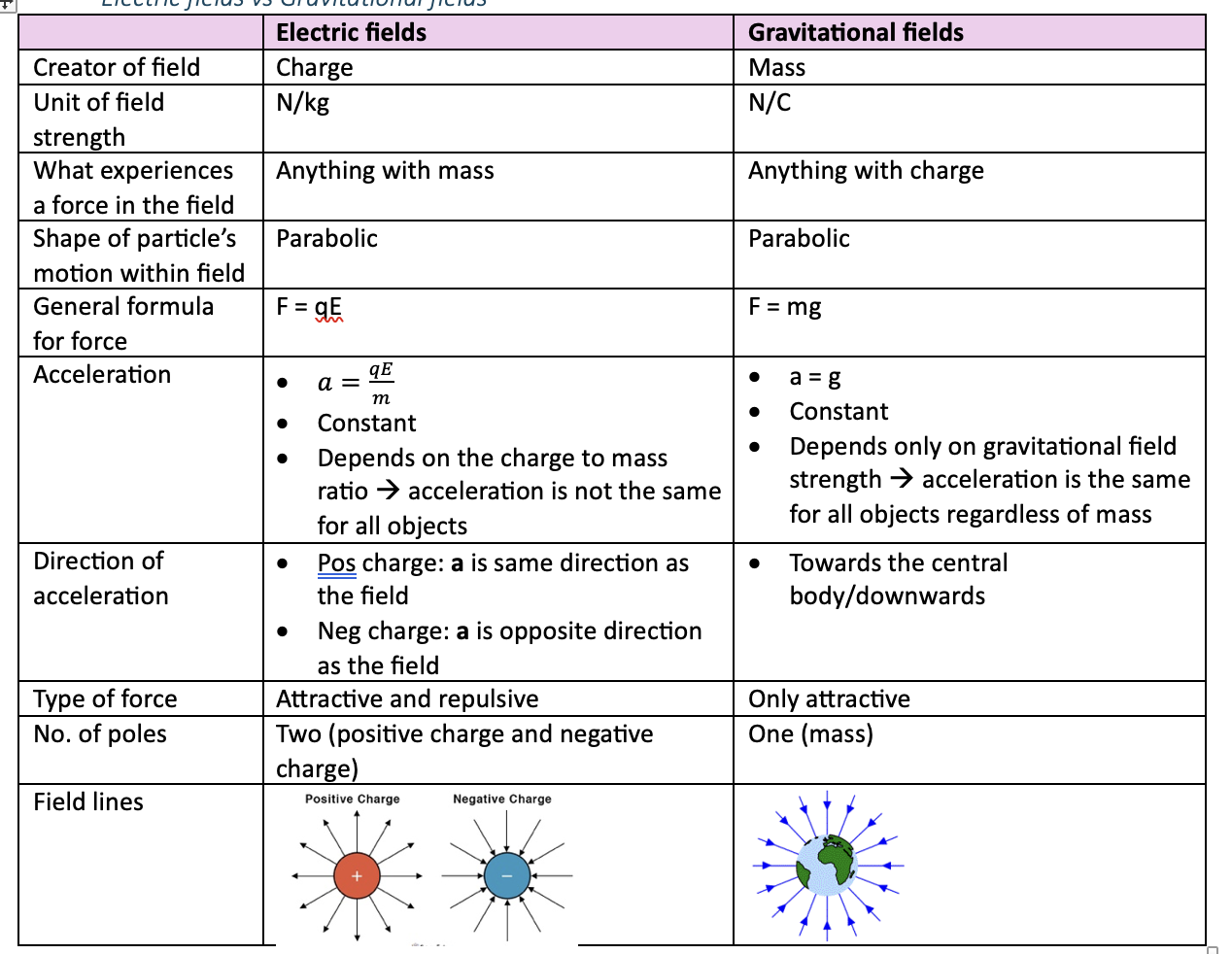
Electric fields vs Gravitational fields

Magnetic fields definition + representation

defined by how a north pole would react

• made by magnets / moving charges

• Leave perpendicular to the surface

• Always forms closed loops

• To indicate the direction

  • Dots and crosses convention (think of shooting arrow)

    • X (cross) = direction of vector is into the page = tail of arrow

    • (dot) = direction of vector out of the page = head of arrow

  • Lines with arrows

    • Arrow points to the left/right/up/down = direction vector is that way

• When two magnetic fields overlap, use vector addition to find the resultant field

Right Hand Rules

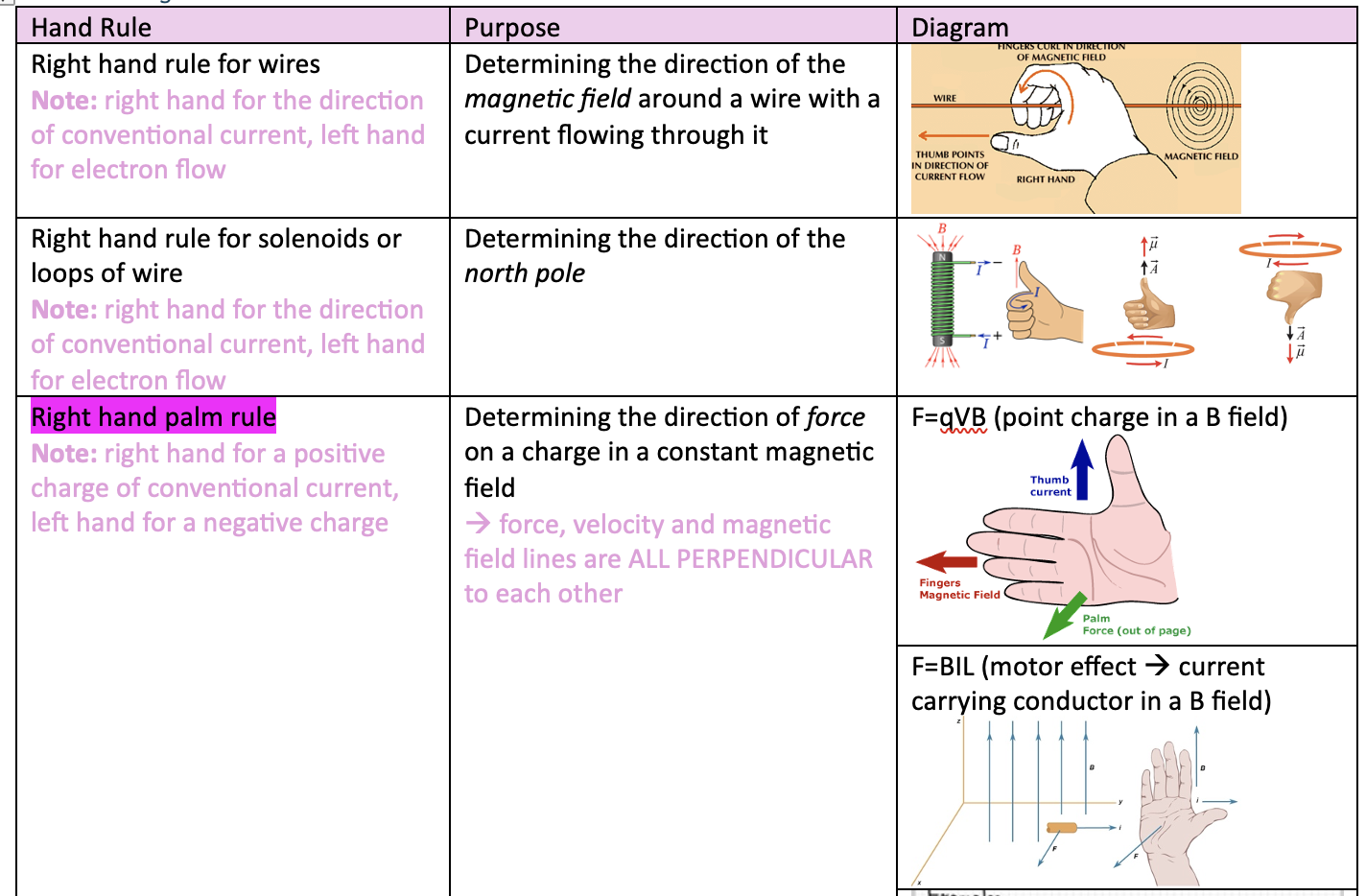
Formula for B for

• current carrying conductor wires

• solenoids

wire:

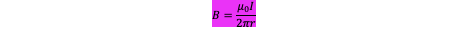
solenoid

ncrease B by:

·      Increasing the number of turns per unit length (decrease length while increasing turns)

·      Increasing current

·      Putting a ferromagnetic material (e.g. soft iron core) in the middle to amplify the field

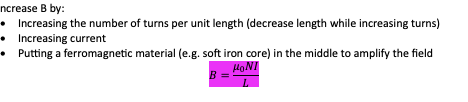
Magnetic Force on a Moving Charge

F=qvB sinθ

→ theta is angle between B and v

A charged particle moving in a magnetic field experiences a magnetic force

• It will NOT experience a force if it is moving parallel to the field

• Maximum force if moving completely perpendicular to the field  sin𝜃 is 1

• No charge = no force experienced

Path of a charged particle in a constant B field

(assume no gravity, unless stated otherwise)

A charged particle will always move in UCM in a magnetic field since it satisfies all the conditions to undergo UCM

NO WORK IS DONE IN UCM = NO WORK IS DONE IN MAGNETIC FIELD

→ KE is constant, speed is unchanged

1. Force is constant because the magnetic field is uniform (F=qvBsin𝜃)

2. Force is always perpendicular to velocity (due to right hand palm rule)

∴ Follows uniform circular motion for as long as it is in the field

Thus, the provider of UCM is the magnetic field

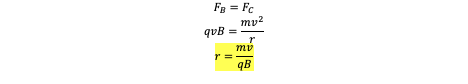
Cathode rays - what is it + how to generally solve qs involving them

Guns that shoot out electrons → generally when they are shot out, they go through a B or E field, which alters their path

1. Two electrodes act like parallel plates to create an electric field (+ to -)

   1. Negative electrode = cathode  where electrons are shot out of

   2. Positive electrode = anode  where electrons are received

2. Work is done between the two electrodes to increase the kinetic energy of the electron (thus the velocity)

   1. Speed at anode if electrons are at rest at cathode:

   2. W = qV = ½mv2  rearrange for v

3. After the anode there can be a magnetic/magnetic field that acts on the charge  causes change in motion

   1. Deflection by magnetic fields - UCM → use RHPR to figure out the direction of deflection

   2. Deflection by electric fields - parabolic → use knowledge of attraction between charges to figure out direction of deflection

4. For the electrons to be undeflected:

   1. Fnet = 0, FB = FE

   2. qvB = qE

   3. E = vB

Comparison of motion in uniform fields: G, B and E

	Gravitational Field	Electric Field	Magnetic Field
Who creates the field	Mass	Charge	Moving charges (currents) or magnets
What experiences the force in the field	Anything with mass	Anything with charge	Moving charges (currents) or magnets
Likely shape of particle’s path in this uniform field	Parabolic	Parabolic	Circular
Reason for shape of path	Force in one direction	Force in one direction	Force perpendicular to velocity, provides centripetal force
General formula for force on particle	F = mg	F = qE	F = qv⟂B
Units of field strength	N/kg	N/C	T
Magnitude of acceleration	a=g → independent of mass	a=qE/m → depends on charge to mass ratio	a=(q/m) vB → depends on charge to mass ratio
Direction of acceleration	In direction of field	In direction of field for pos charge Opposite for neg charge	According to right hand palm rule for positive charge. Opposite for negative charge.
Is work done	Yes (for parabolic motion) No (if in circular orbit)	Yes (parabolic motion = K changes)	No (due to UCM)

Comparison of uniform circular motion: G and B

	Orbital motion around a planet	UCM in a magnetic field
Field	Gravitational field of the planet	Uniform magnetic field
Shape of field	Towards centre of planet	Uniform, constant direction
Shape of path	Circular (no work)	Circular (no work)
Reason for shape of path	Gravitational force is towards the central body while velocity is tangential	·      Magnetic force perpendicular to velocity ·      Force is constant
Provider of Fc	Gravitational force	Magnetic force
General formula for force on a particle	F=GMm/r²	F=qvBsin theta
Condition for UCM	Fc=Fg v=√GM/r	Fc=Fb r=mv/qB
Magnitude of acceleration	a=g	a=(q/m)vB
Direction of acceleration	In direction of field	In direction of field for pos charge Opposite for neg charge