Week 3- Fixed .vs. random effects; Effect size

10/10/24

Detecting effects

Raising the sample size we increase the statistical power of a test to detect an effect

Fixed vs random effects- ANOVA decided

Fixed effects

• Fixed effects analyses are used when you want to know whether the individual and precise conditions tested have an effect on performance

  • we are only interested in the specific levels of the IV featured in the dataset

  • F-ratio calculation takes the error term from within those groups/conditions defined by that specific IV

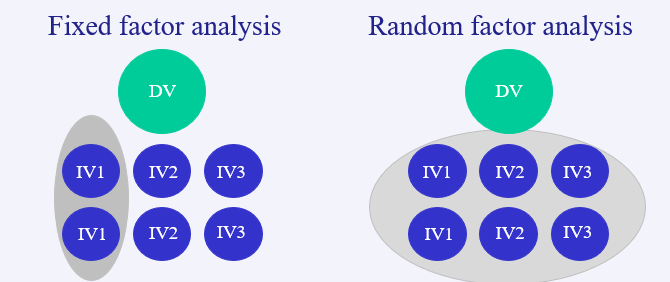
Random effects

• Random effects analyses are used when the values of the experimental conditions have been sampled at random from a wider population of different

  • We want to generalise the observed effect to other possible levels of the IV

  • F-ratio calculation takes the error term from the whole sample (i.e. all groups/conditions defined by all IVs in the design)

• For Random effects, the concern is more with the effects of varying the dimension under investigation than with the specific values tested in the study

Random effects- issue

• Jamovi looks at all participants in all possible conditions for the F ratio, and so the error term is larger

• A bigger error term represents more signal noise , and so a random effect test is less likely to be significant due to worse signal/noise ratio.

• This is because we are trying to generalize findings here to variables we haven’t even tested

Fixed or random effect example

• C1 and C2 fixed as the different forms of presentation are unlikely to have been sampled at random from a list of different possibilities

• D1-3 may be random if the delay values were chosen randomly to just see how delay affects performance, and could be changed to any values

  • Fixed if they’re interested in the effects of those specific delay values, based on a theoretical or experimental reason

Random .vs. fixed effect uses

• Random is often used when testing something brand new e.g. when MSM was being developed

• Fixed effects have an advantage as they’re more likely to be significant

• However, fixed cannot be generalised beyond the levels chosen

Random effects issue- assumptions

• Assumes that the relationship between the IV and the DV is consistent throughout the full range of possible values of the IV

• The relationship may only be consistent for part of its range or have 2+ distinct relationships that are consistent within particular ranges

Fixed .vs. random examples

• Gender: male vs female vs non-binary- Fixed

• Treatment: CBT vs Mindfulness vs No therapy- Fixed

• Primed condition: Aggressive vs Friendly vs No prime- Fixed

• Location:  London vs Liverpool vs Exeter- potentially both (specific locations- fixed, regional- random)

• Age:  5yrs vs 11yrs vs 16yrs (if we were interested in UK school stages)- both (specific age- fixed, key stage- random)

• Age:  5yrs vs 10yrs vs 15yrs (if we were interested in general development)- both (specific age- fixed, development period- random)

Participants are…

Almost always treated as a random effect- want to generalise results from a specific person to a general population

Effect size and statistical power

The power of a statistical test is the chance that it will allow you to declare the existence of a main effect (or interaction) that is genuinely there in the data

Statistical power

• Expressed in terms of a probability value-

  • Power = 1.0 implies that there is 100% chance that the test will detect the effect (if it does exist). In psychology, 80% is our benchmark

  • Power = 0.0 means that there is absolutely no chance of detecting the effect

Effect size

• Reflects the strength of the influence of the IV on the DV

• Larger effect size means bigger differences in DV between groups defined by the IV

• Larger effects are more visible, easier to detect

Effect size .vs. significance

Effect size is the magnitude of the observed effect, while significance only tells us that an effect exists

Power and effect size

• More powerful analyses allow you to detect smaller effect sizes

  • Large effect sizes only need relatively low power analyses to detect them

  • Small effect sizes need more powerful analyses to detect them- more data points in each group, the more powerful the analysis

• Up statistical power → up sample size (reduces error variance, but if there’s nothing to find then this obviously won’t work)

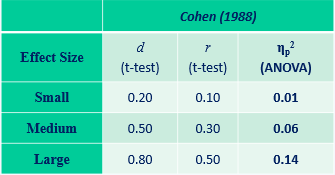
Different effect size measures- interpretation

General estimates, but they are arbitrary and we accept different effect sizes in different disciplines (e.g. pharmaceuticals see small effect sizes as large as in general, their sizes are small)- we will use partial eta squared and we always need to include effect size

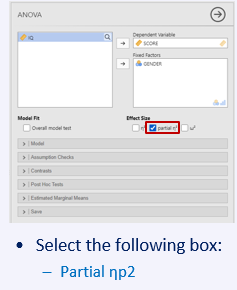
Calculating effect size in Jamovi

• Partial eta squared (η_p²) is reported after the p-value

• Standard formula: F(1,8) = 12.82, p = .007, η_p² =.62 (large- above 0.14)

Calculating power using Jamovi

• Using G*Power- separate from Jamovi, a free software to install

• Allows power estimates for complex study designs (not going to assessed this year, but will be used later in our course)