Reintroducing Inferential Statistics

p: Assume Dr. Null is correct and there was zero
relationship between our variables in the
population, p is the probability we would obtain a
random sample with a relationship between
variables that’s at least as strong as the relationship
we found in the current sample.

More concisely: If there is zero effect in the
population, we would find the observed effect (or a
larger effect) in [p*100]% of random samples.

What’s the ppint of inferential stats?

To use sample data to make a conclusion (an inference) about the entire population

To get research published, the p values for you effect needs to be? 

p < .05 

ONE-SAMPLE T-TEST 

When do we use it?
Is the sample mean significantly different from a set, pre-determined number?

Examples…
1. Is the mean NU-psych IQ significantly higher than the population mean IQ of 100?

2. Is the mean high school GPA of NU students significantly different from the nationwide (population mean) high school GPA of 2.8? 

3. Can the average person hold their breath for more than 30 seconds? 

INDEPENDENT-SAMPLES T-TEST 

When to use it?
For some numeric variable, is the mean among Group 1 significantly different from the mean Group 2?

Examples…

1. When it’s time for a meal, who takes longer to decide to what to eat, men or women?

2. Is the importance of your favorite musicians’ authenticity (1=NOT-IMPORTANT to 7= EXTREMELY-IMPORTANT) significantly different between hardcore Drake fans and hardcore Kendrick Lamar fans?
   3. Is the mean number of Instagram followers significantly different between people over 50 and people under 25?

Paired-samples t-test aka DEPENDENT-MEASURES, REPEATED MEASURES,WITHIN GROUPS 

Paired, they depend, you need to repeat, groupies 

When to use it?
Scenario 1: is a “before” score significantly different from an “after”?

Examples…

1. When people have a headache, will they report reduced pain symptoms 30 minutes after (vs before) taking an ibuprofen?

2. Do people average more car accidents during the year before (vs during the year after) they complete a defensive-driving course?

3. Do people with ADHD perform better on an attention test after they take adderall, compared to on a day when they haven’t taken addreall?

Paired-samples t-test aka DEPENDENT-MEASURES, WITHIN-GROUPS

Scenario 2: Test for differences between two similarly-scored variables 

Examples…

1. Do NU students score significantly higher on the ACT math section, compared to the ACT reading section? (Both scored out of 36 total)

2. All else equal (eg. looks, income, etc) is the perceived attractiveness of a flat-earther significantly different than the perceived attractiveness of a STEM major? (both scored on a scale from 1=unattractive to 5= attractive) 

Bivariate Correlation & Line Regression Analyses

When to use it?

As numeric variable #1 increases, deos numeric variable #2 tend to increase or decrease?

Examples…

1. As people get older do they tend to become more conscientious?

2. As people exercise more hours per week, do they tend to have fewer depressive symptoms? 

3. As people give more high fives per day, do they tend to report higher levels of life satisfaction?

Context non-specific definition of p…

If the null hypothesis were true, we would find the effect we found - or a larger effect in p of random samples from the population

Null Hypothesis 

The hypothesis that there is no significant difference between specified populations, any observed difference being due to sampling or experimental error 

Chi-sqaure (χ²) test for independence

When to use it?
Given categorical variable A-vs-B and categorical variable X-vs-Y… When people are members of category A (vs B), is it more likely that they’re also members of category Y (vs X)?

Examples…

1. If you prefer dogs (vs cats), are you more likely to be an extravert (vs introvert)?

2. If you are a STEM major (vs not) are you more likely to be a frequent video gamer (vs not)?

3. If you enjoy cooking (vs don’t) are you more likely to have a BMI <30 (vs BMI>30)?

One-way Analysis of Variance (ANOVA)

When to use it?

• For numeric variable, is the mean among Group 1 significantly different from the mean among Group 2 (vs Group 3, vs Group 4, etc.)?

• ANY situation where you can use independent-samples t-test, you can also use one-way ANOVA

→If testing between 3 or more groups, you can use one-way ANOVA but NOT independent-samples t-test

Examples…

1. Is the average IQ different between Democrats, Republicans, or Independents?

2. Is GPA different between psych, BNS, or engineering majors?

3. Alcohol consumption different between 1st, 2nd, 3rd, 4th years?

2×2 Factorial ANOVA 

When to use it?

Assessing how a numeric variable differs between two different 2-level categorical variables 

Examples…

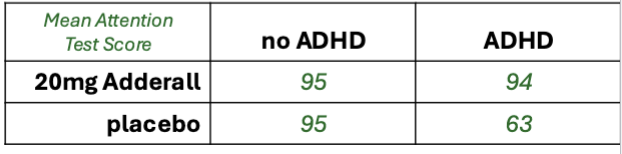
1. Factor 1: ADHD (yes vs no) 

2. Factor 2: Adderall (20mg vs placebo) 

Outcome variable: Attention Test score 

• Above, did ADHD (present vs not) influence attention scores?

• Or, did Adderall (20mg vs not) influence attention scores?

2. Factor 1: pre-bed screentime (yes vs no)

Factor 2: pre-6pm cardio exercise (20 min vs none)

Outcome variable: time elapsed between sleep attempt and sleep onset

3. Factor 1: alcohol drinker vs not

Factor 2: male vs female

Outcome variable: Autobiographical History of Violence Score

What can 2×2 Factorial ANOVA tell you?

Whether there was an INTERACTION EFFECT

• aka MODERATION

• INTERACTION EFFECT: When the effect of one independent variable on a dependent variable changes depending on the value of another independent variable 

Z-scores helpful vs when they’re limited

As a tool for understanding where a score falls within a normal distribution, z-scores are helpful
When, however, is the utility of z-scored limited?

• They don’t work with non-normal distributions

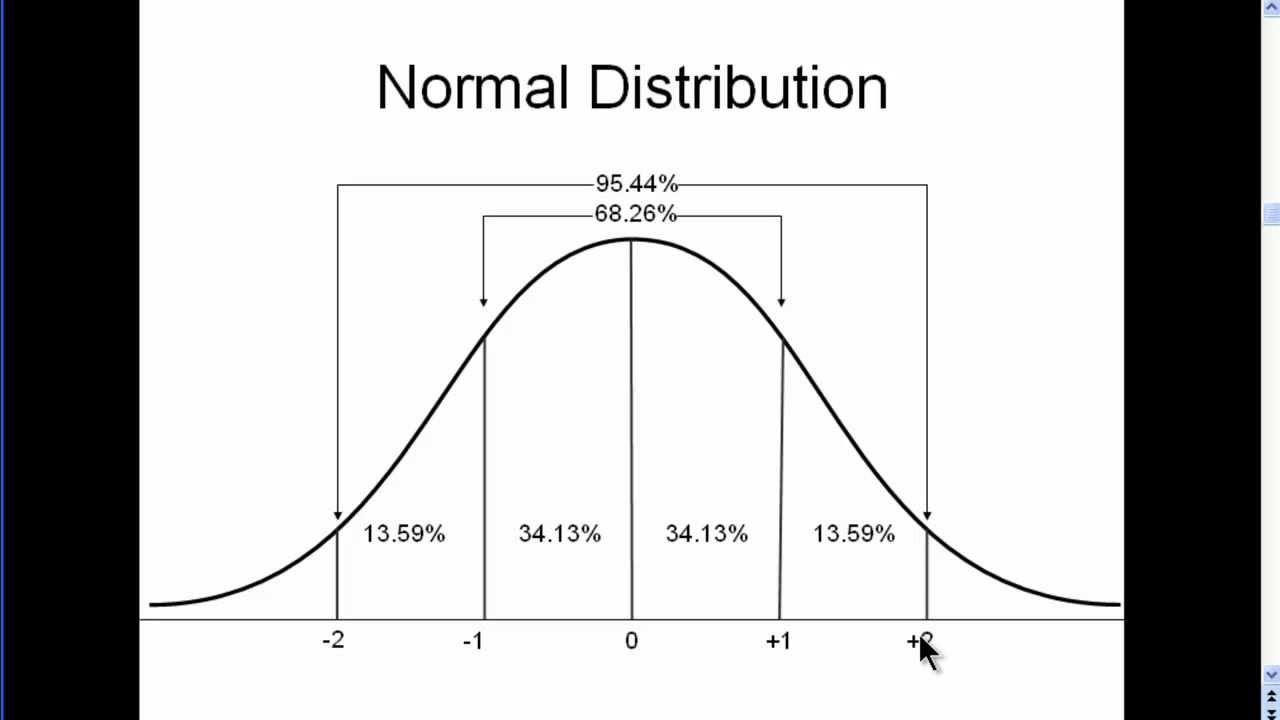
Normal distribution

Bell-shaped curve where most data points cluster around the mean, and the frequency of values tapers off symmetrically toward the tails

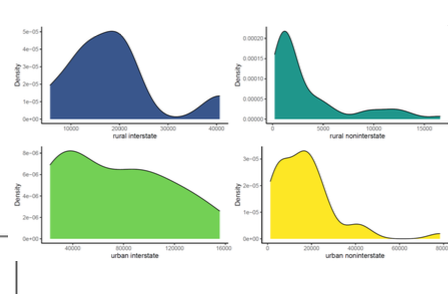
Non normal Distribution

Data that doesn’t follow the symmetrical, bell-shaped curve of a normal (or Gaussian) distribution 

Inferential Statistics 

Use patterns of data within a sample to make probabilistic about patterns of data within the entire population 

i.e they use data from a few dozen people (or more) to make conclusions about millions!

CENTRAL LIMIT THEOREM (secret sauce of inferential stats)

For a given variable, even when the distribution of raw data is non-normal, the sampling distribution of several sample means will always approach normality 

In other words, you’ll ALWAYS end up with a normal distribution if you make a histogram of a crap-ton of sample means for a variable 

CENTRAL LIMIT THEOREM DETAILS

• More sample means → closer to a normal distribution of means 

• higher N per sample mean → closer to a normal distribution of sample means 

• higher N per sample mean → a narrower distribution of sample means 

Why/how is CLT the “secret sauce” of inferential stats?

Because we know the distribution of sample means is always normal… once we have one sample mean, we can make confident, probabilistic predictions about the population mean 

Standard Error of the Mean

(SE) = the standard deviation of sample means

Per CLT, there is always a normal distribution, so the z-score rules always apply! 

SE is rarely truly knowable or known.. but… 
To estimate (“calculate”) SE:

SE = SD/square root nx

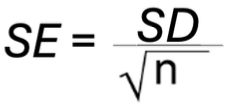
Using CLT, SE, and the sample mean to make an inference about the population mean 

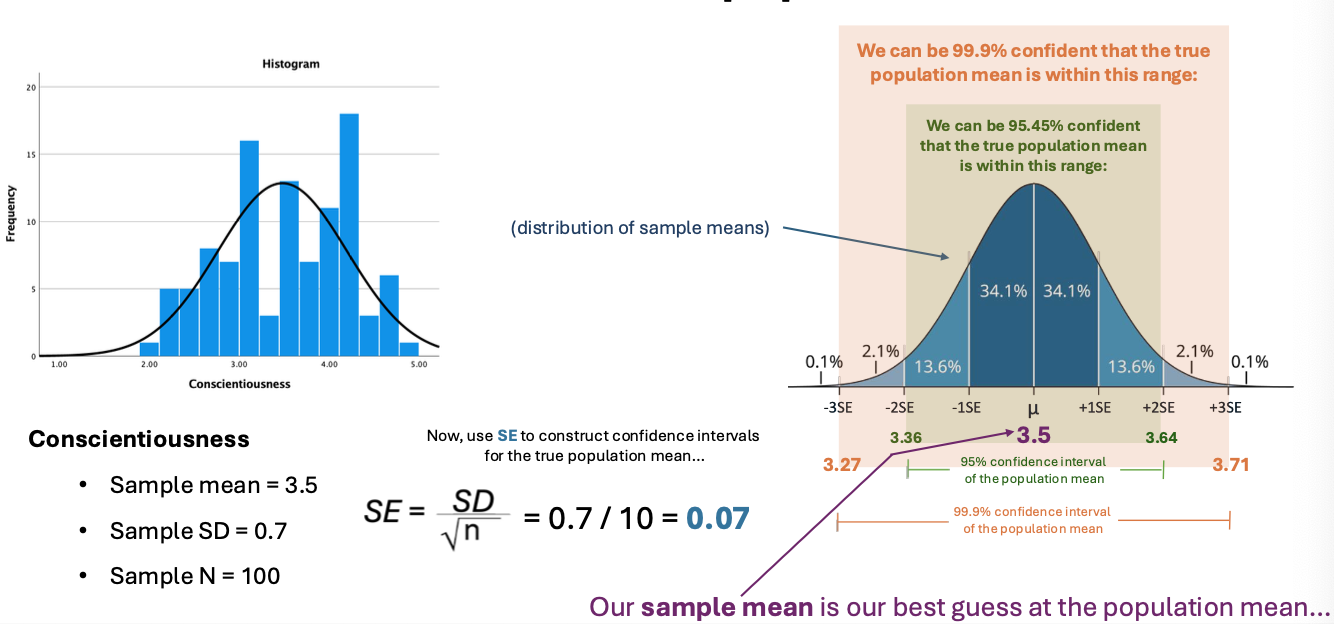
What is the Central Limit Theorem? What are the “extra details”?

Central limit theorem states that for a given variable, even when the distribution of raw data is non-normal, the distribution of several sample means will always approach normality 

Detailes: 

1. More sample means → closer to a normal distribution of means

2. higher N per sample means → closer to a normal distribution of sample means

3. higher N per sample means → a narrower distribution of sample mean s

What is Standard Error of the Mean (SE)?

Standard deviation of all possible sample means that could be drawn from a population

• it estimates the range within which a population mean is likely to fall

SE equals SD over the square root of n

How are CLT and SE used to make an inference about the population mean from the known sample mean, SD, and N?

CLT: sampling distribution of mean is (ˉx) is ~normal if n is large, centered at μ (population mean) 
SE: Se = S/square root of n; measures variability of sample mean 

Standard notation for expressing the probability of an outcome is…

p(outcome) = ____ ← (the blank is a decimal between 0.0 → 1.0)

Formula for probability is…

p(outcome) = (number of independent results that would qualify as outcome) / (number of possible outcomes for the event)

Ex. p(random item from my pocket is a phone) = ¼ (4 being phone or kets or mint or chapsticks) = 0.25

CONVERTING PROBABILITY INTO PERCENTAGE…

MULTIPLY BY 100: 0.25 → 0.25×100 → 25% chance 

Mutually exclusive 

Two outcomes are mutually exclusive if it would be impossible for both outcome to happen 
For example 

• A coin can’t land on both head and tails

• A football team can’t both win and lose 

OR (add) vs AND (multiply)

When calculating the probability of MUTUALLY EXCLUSIVE outcome1 OR outcome2, ADD (+)…

Example: What’s the prpbabiltiy of rolling 2 OR 4 OR 6?

• p(2 or 4 or 6) = 1/6 + 1/6 + 1/6 = 3/6 = 0.5 

For p of MUTUALLY EXCLUSIVE outcome1 AND THEN ALSO outcome2, MULTIPLY (*)….

Example: What’s the probability of rolling 2 AND THEN 4 AND THEN 6?

• p(2, and then 4, and then 6) = p(2) x p(4)  x p(6) = 1/6 × 1/6 × 1/6 = 1/216 

Gamblers Fallacy

Our tendency to assume a certain independent outcome is “due”, because this outcome has not occurred for several prior identical independent event 

Hot-Hand Fallacy

Tendency to assume that a certain independent outcome is “on a roll”, because it was the result of several prior independent events

Expected Value

If you could make the bet 10-trillion times, what would be the avg outcome?

EV= [value of outcome1] x [p(outcome1)] + [value of outcome2] x [p(outcome2)] 
(same formula written more concisely) EV = o₁ x p₁ + o₂ + p<sub>2

Examples 
Flip a coin. If it’s heads, you win $2. If it’s tails, you lose $1 
EV = [$2 × 0.5] + [=$1 x -.5] = $1 + [-$0.50] = $0.50</sub> 

P-value 

How likely it is to get same results by random chance

If p is less than 0.05, you reject the null hypothesis