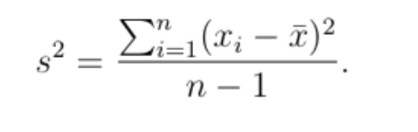Stats 201 notes

What is Statistics?

The art and science of designing studies and anlayazing data

Data analysis

The process of organizing, displaying, summarizing, and asking questions about data

Steps of data analysis

step 1: pose a question that can be answered by data

step 2: determine a plan to collect the data

step 3: summarize the data with graphs and numerical summaries

step 4: answer the question pposed in step 1 using the sata and summaries

What is data?

The information we gather with experiments and surveys. That is, data are numbers with a context.

What are the 3 components of statistics

1) design

2) Description

3) Infernence

What is design?

Planning how to obtain data to answer the question of interest

What is descriptive?/Descriptive Statistics

summarizing and analyzing the data obtained. can use numbbers or graphs

What is inference?/Statistical Inference

Making decisions/conclusions and predictions based on the data to answer the statistical questions

Individuals (the who)

objects (people, animals, things) described by a set of data

Variables (the what)

any characteristics of an individual. A variable can take different values for different individuals. They are 2 types

What are the 2 types of variables in stats?

categorical/qualitative and quantitative

Categorical/Qualitative variable

places individuals into one or several groups oe categories

Numerical/ Quantitative variable

Takes numerical values for which arithmetic operations such as addition and averaging make sense

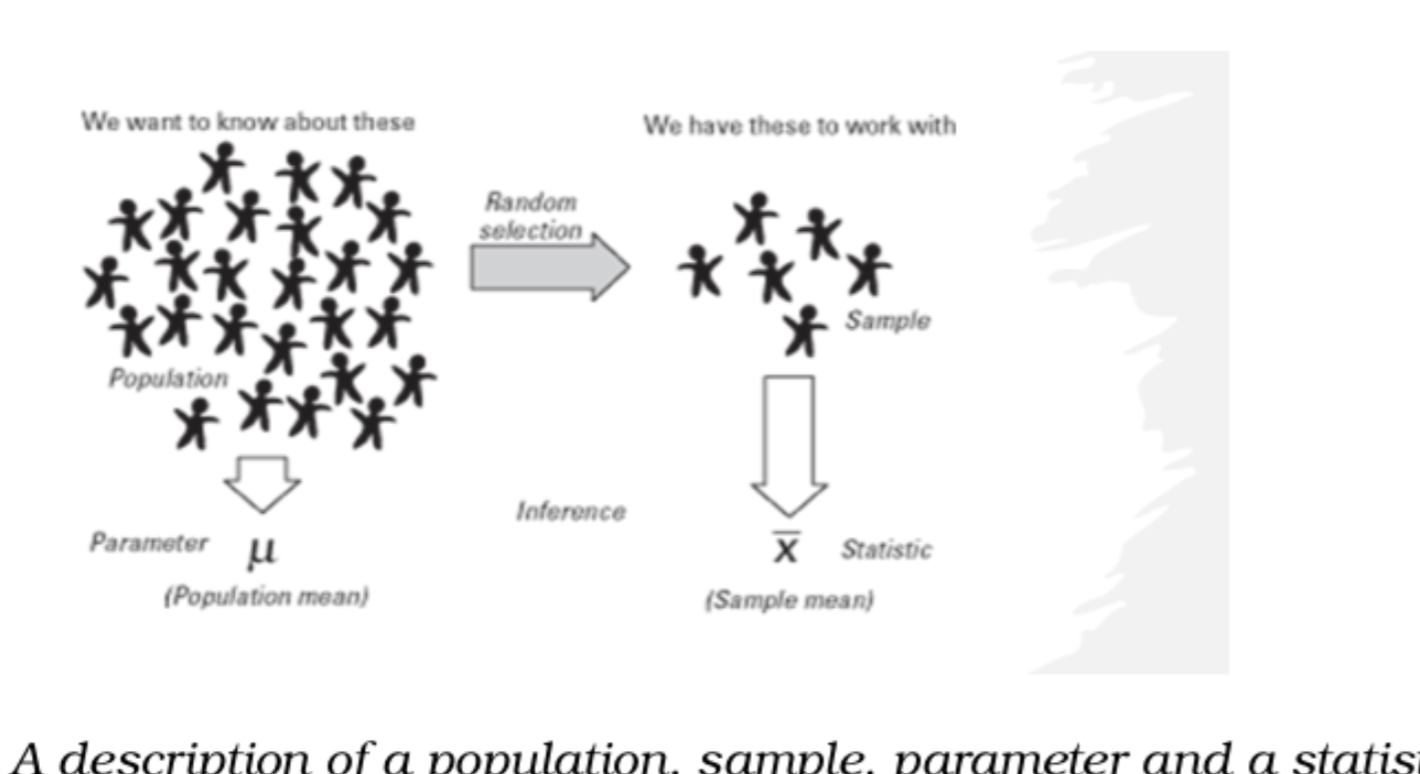
Population

a group of subjects or people we wish to study. ALL is the keyword

Sample

A collection/ subset/ part of objects or people taken from the population of interest

Census

a survey that measures every member of a population

Statistic

a numerical measure/ vaule that characterizes/ describes some aspect of the sample

Description of a population, sample, parameter, a statistic

We use sample statistics to what?

estimate population parameter vaules

A polling agency takes a sample of 1500 American citizens and asks them if they are lactose intolerant. 12% say yes. This is interesting, since it has been shown that 15% of the population is lactose intolerant.

What is the population

all american citizens

A polling agency takes a sample of 1500 American citizens and asks them if they are lactose intolerant. 12% say yes. This is interesting, since it has been shown that 15% of the population is lactose intolerant.

What is the sample

1500 American citizens surveyed

A polling agency takes a sample of 1500 American citizens and asks them if they are lactose intolerant. 12% say yes. This is interesting, since it has been shown that 15% of the population is lactose intolerant.

what is the individuals of the survey

American citizens

A polling agency takes a sample of 1500 American citizens and asks them if they are lactose intolerant. 12% say yes. This is interesting, since it has been shown that 15% of the population is lactose intolerant.

what is the variable

lactose intolerance

A polling agency takes a sample of 1500 American citizens and asks them if they are lactose intolerant. 12% say yes. This is interesting, since it has been shown that 15% of the population is lactose intolerant.

is the variable qualitative (categorical) or quantitative (numerical)

catergorical

A polling agency takes a sample of 1500 American citizens and asks them if they are lactose intolerant. 12% say yes. This is interesting, since it has been shown that 15% of the population is lactose intolerant.

What is the parameter

15%

A polling agency takes a sample of 1500 American citizens and asks them if they are lactose intolerant. 12% say yes. This is interesting, since it has been shown that 15% of the population is lactose intolerant.

What is the statistic

12%

Descriptive statistics

involves methods of organizing. picturing and summarizing information from samples or populations

-graphs and numbers such as averages and percentages

-reduces data to simple summaries without distorting or losing much information

Inferential statistics

Methods of making decisions or predictions about a population, based on data obtained from a sample of that population

-used when data are available from a sample only, but we want to make a decision or prediction about the entire population

Randomness in stats

refers to the inherent uncertainty in the outcome of a process, even when the process is well understood

-Individual outcomes are unpredictable

-long-run patterns may still be stable

Examples of randomness in stats

tossing a coin, daily number of er vists selecting a random sample etc.

Varaibility in stats

describes how much data values differ from one another

-measures the spread in a dataset

-exists even when data are collected carefully

Randomness in a proces leads to

variability in observed data

Observations

data values observed for a variable

In a graph variables are on

the columns (vertically)

In a graph, observations are on

rows (horizontally)

Two Types of variables/data

categorical and quantitative

Categorical

data/variable that places an individual into one or several categories

Quantitative

data/variable takes numerical values for which arithmetic operations such as adding and averaging make sense.

To determine if a variable is categorical or quantitative

Two types of quantitative variables are

discrete and continuous

Discrete

those quantitative variables where possible values form a set of separate numbers. key phrase “the number of “

-outcomes are counts (for example 0,1,2,3)

-no decimals allowed

-finite(not infinite) number of possible values

Examples of discrete

number of pets

number of siblings

number of friends

Continuous

those quantitative variables where possible values form an interval

-outcomes are measurements

-Decimals are allowed but not required

-infinite number of possible values

Examples of continuous

Hieght, weight age, time taken to complete an exam

Two types of catergorical variables

nominal and ordinal

Nominal

a categorical variable that has two or more categories, but there is no intrinsic ordering to the categories

Examples of nominal

hair color, gender , country

Ordinal

A categorical variable that has a clear ordering of the variables

Example of ordinal

Economic status (low, medium, and high)

level of education (elementary, high, and college, etc.)

Financial happiness (very happy, happy, neutral, unhappy, very unhappy)

What is ditribution of a variable?

A distribution that tells us what values it takes and how often it takes these values

What to look for with quantitative variables

shape

center

spread

Shape

do observation cluster in certain intervals and / or are they spread thin in other areas

Center

where does a typical observation falll

Spread or variability

how tightly are the observatuiobs clustering around the center

Explortaory data analysis

statistical tools (such as graphs to display a variable) and ideas to examine the data in order to describe their main features

What are the types of display for categorical data / variables?

1) Frequency table

2) Bar charts and pie charts

3) Paerto chart

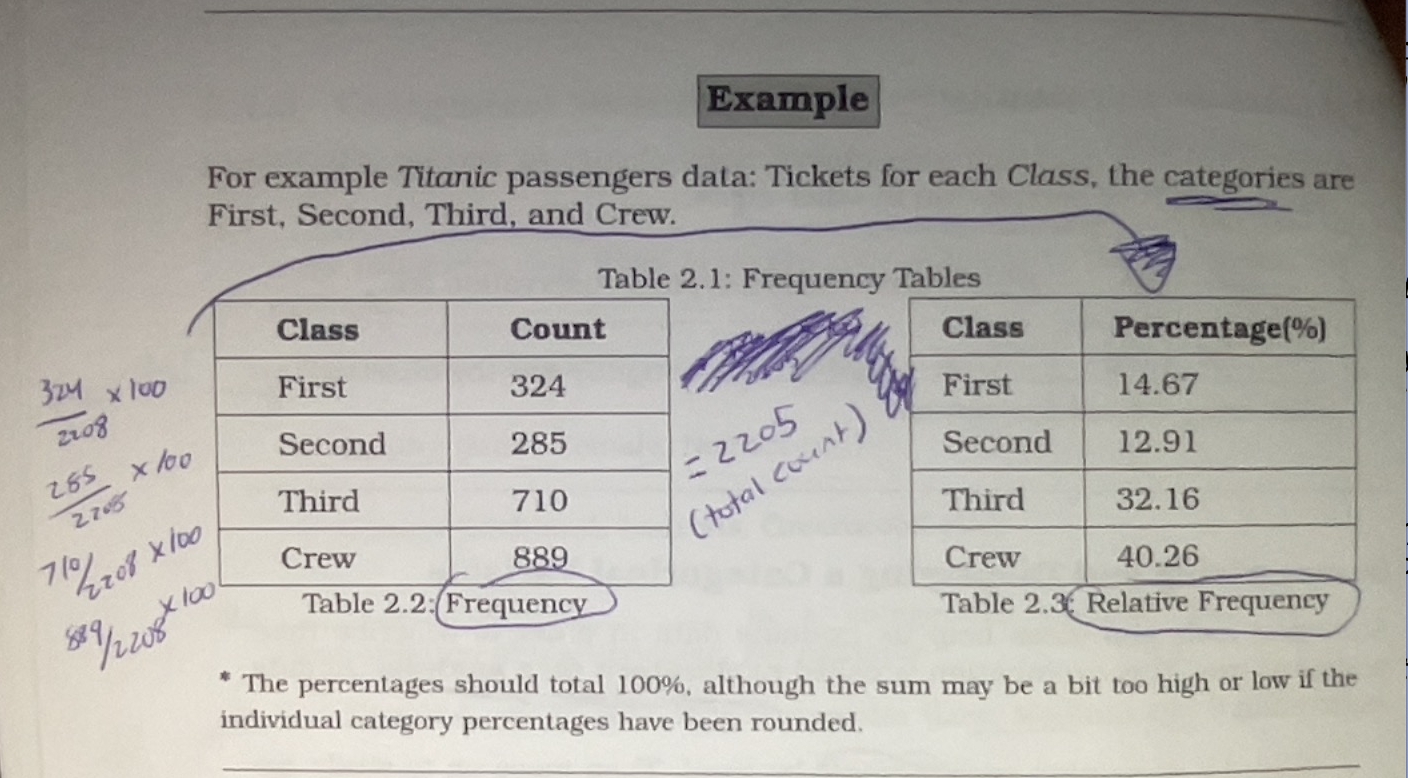
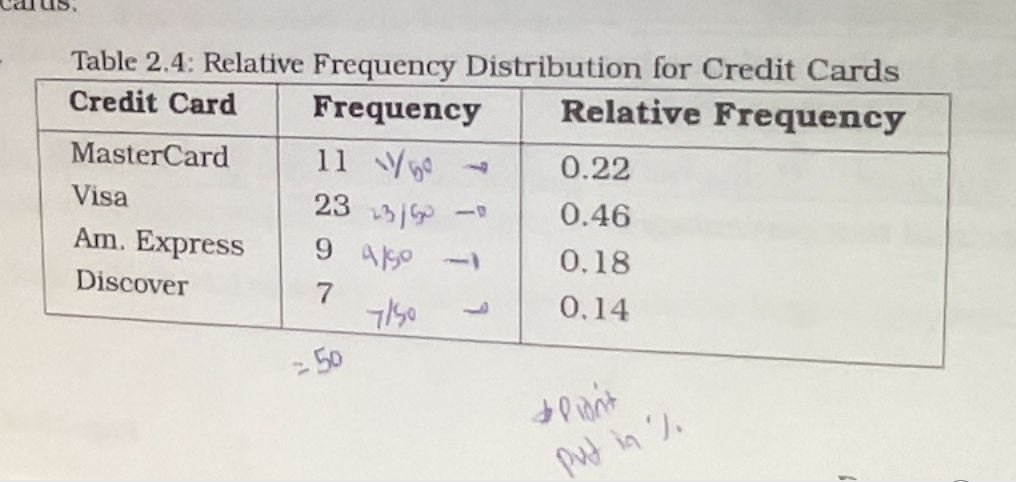
Frequency Table

A table that lists the number of cases in each category along with its name.

Frequency

Number of observations for each value, the counts

Relative Frequency (R.F.) / Proportion

number of observation in each category divided by the total number of observations

Percent proportion

proportion multiplied by 100 ( changing the decimal to a percentage)

Example of a frequency table

Pie chart

A circle having a slice of the pie for each category. Wherethe size of slice corresponds to the percetnage of observation in the category

Bar chart

Displays a vertical bar for each category. The height of the bar shows the percentage of observations in the category. Usually each bar is apart

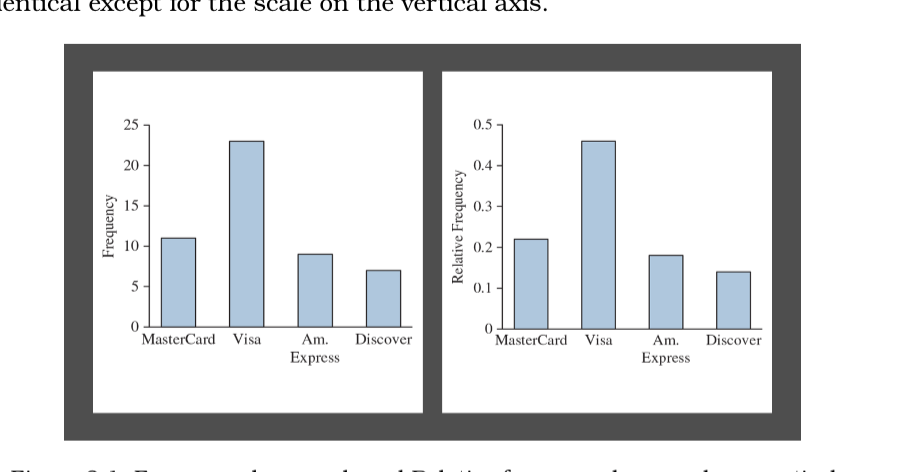
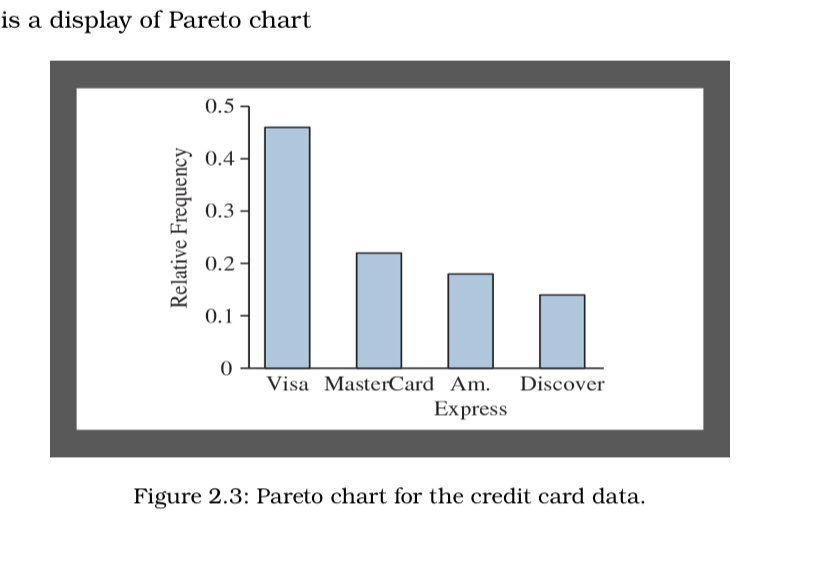
Pareto chart

A bar chart in order from largest to smallest frequency or relative frequency

What are the types of display for quantitative data / variables?

1) Dot plot

2) Stem and leaf plot

3) Historgram

Dot plot

Shows a dot for each observation, placed just above the value on a number line for that observation.

-each dot represents one observation

-stacked dots indicated repeated values

-best for small to moderate-sized datasets

What do dot plot show

center (typical value)

spread (range, clustering)

shape (skewness, symmetry)'

outliers

Dot plot advanatges

simple and easy to interpret

preserves individual data values

Stem and leaf plot

organizes numerical data by separating each value into a stem (leading digit(s)) and a leaf (final digit

-stems are listed vertically

-leaves are listed horizontally in ascending order

-original data values can be reconstructed

Stem and leaf plot advantages

Steaf and leaf plot disadvantages

not suitable for data with wide ranges or many digits

difficult to compare multiple data sets

Histogram

A graph that uses bars to represent the frequencies or the relative frequencies of the possible outcomes for a quantitative variable. Most common graph.

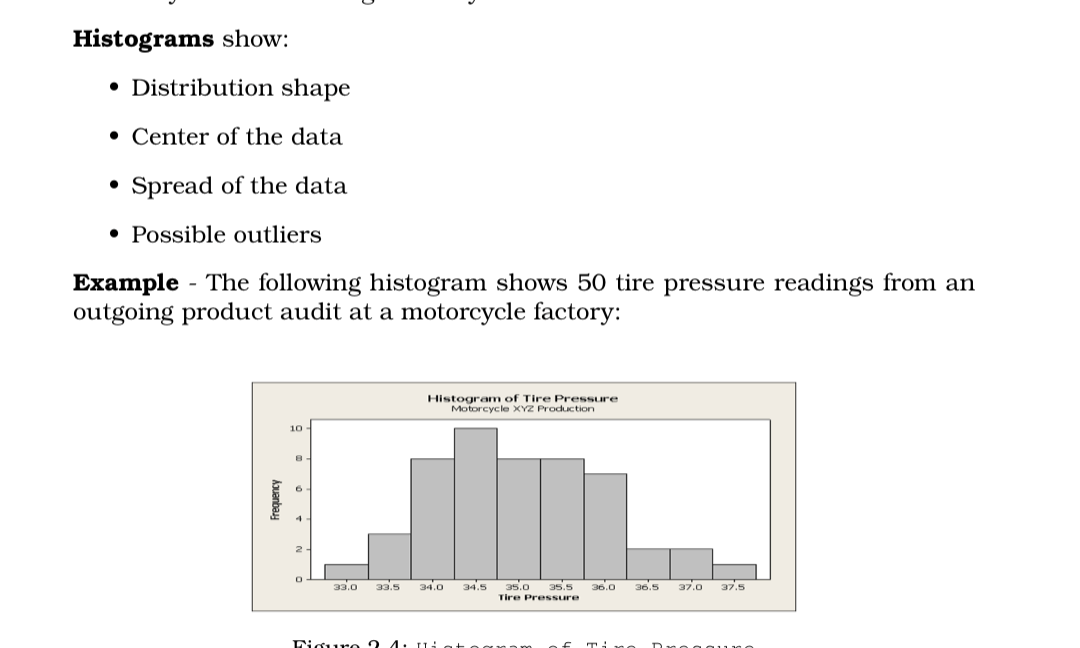
*The bars touch, and exact data are not visible. however effective for large datasets

• you can describe the overall pattern of a histogram by its shape, center, and variability

How is the shape of a distribution described for a historgram?

by its number of peaks and possession of symmetry (skew or not)

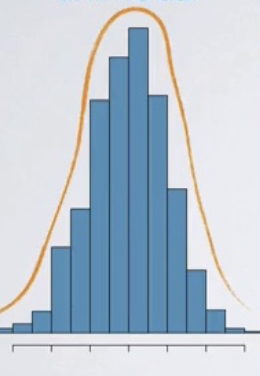
Symmetric distribution

A bell-shaped, a distribution where the right and left sides of the histogram are approximately mirror images of each other

Skewed right / positive skew

a distribution where the right side extends farther out than the left side

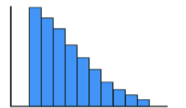
skewed left / negative skew

a distribution where the left side extends farther out than the right side

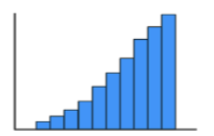
Mode

most common value in a data set

unimodal

one peak in the data

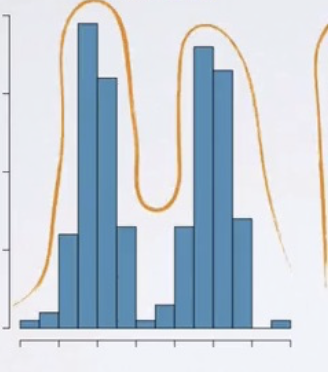
Bimodal

two peak in the data

measures of the center of a quantitative data

1) mean

2)median

1) Mean

The average of the data. The most commonly known and frequently used measure of center.

To find the mean, divide the sum of observed values by the number of observations

Sample mean (mean of a sample) symbol

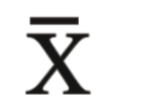
Population mean symbol

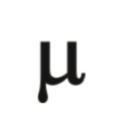
Basic properties of the mean

-also known as the balancing point

-If the collection consists of values of a variable measured in specified units, then the mean has the same units too

-Usually, the mean is not equal to any value that was observed in the sample

-for skewed distributions, the mean is pulled in the direction of the longer tail

-MEAN IS SENSITIVE TO OUTLIERS (unusaully large or unusaully small observation)

2) Median

The midpoint (middle) of a distribution from smallest to largest

*If there is one center observation, the median is the center observation in terms of the ordered list

*If there are two center observations, the median is the average of the two center observation

Property of median

It is a resistant measure of center. It is resistant (robust) to extreme observation, which has little, if any, influence on its value, such as outliers.

good choice of measure of center when outliers are present

Mean vs Median example

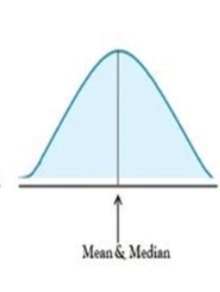
If a distribution shape is perfectly symmetric, the mean and median are?

The mean equals the median

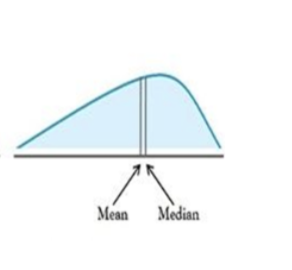
If a distribution shape is skewed to the left,the mean and median are?

The mean is less than the median

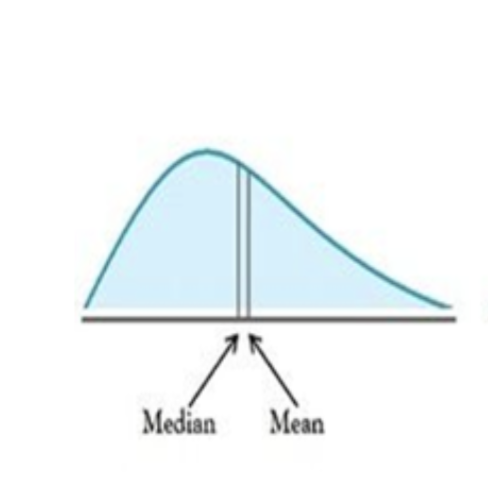
If a distribution shape is skewed to the right, the mean and median are?

The mean is greater than the median

Which choice of measure of center is best if the distribution is highly skewed

The median

Which choice of measure of center is best if the distribution is symmetric or one midly skewed

The mean

Which choice of measure of center is best if comparing a distribution that is one symmetric and one skewed

Median

Mode

The value that occurs most frequently

*for categorical data, it is the category with the highest frequency

*for discrete quantitative data, the value that occurs most often

*continuous quantitative data, usually not meaningful to look for the mode because there can be multiple modes or no mode at all

Example of mode

Measure of variability of quantitative data

1) Range

2) Standard deviation

3) variance

4) IQR

Variability

describes how far apart data points lie from each other and from the center of a distrubution

Range

The difference between the largest and the smallest value observations in a data set.

*however not a good measure of spread because it ignores other values in the data set, and it is affected by outliers-that is, range is not a resistant statistic

Deviation of an observation x from the mean x-bar is …

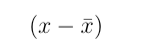
Sample Variance

The average squared deviation