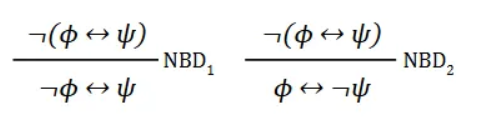8.1 Natural Deduction

What are the Disjunction Introduction rules?

Showing ϕ ∨ ψ by either showing ϕ or ψ

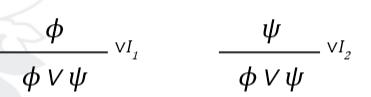
Use: ϕ / (ϕ ∨ ψ)

Given ϕ = “I have a pencil”, and ψ = “I have a pen”

And what natural deduction rule is this?

“I have a pencil” is sufficient to demonstrate “I have a pencil or a pen”

vI₁ ← Disjunction Introduction 1

What is modus pones? And what natural deduction rule does this fall under?

The method of affirming

“If i know ϕ, and I know that ϕ implies ψ, then I can deduce ψ.”

Conditional Elimination

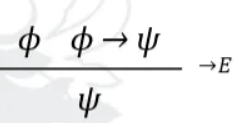
What is modus tollens? And what natural deduction rule does this fall under?

The method of denying

“If ϕ → ψ and ψ is not true, then ϕ is not true”

Conditional Elimination

Using Where ϕ = “I go to the supermarket” and ψ = “I buy milk”.

Give an example of modus pones

”If I go to the supermarket, I will buy milk. I went to the supermarket. Therefore, I bought milk.”

Using Where ϕ = “I go to the supermarket” and ψ = “I buy milk”.

Give an example of modus tollens

”If I go to the supermarket, I will buy milk. I did not buy milk. Therefore, I could not have gone to the supermarket.”

Using modus pones:

Argue: P → Q → R, P, Q ⊢ P ∧ R

What are the double negation rules?

Double negation can be eliminated and introduced

Give an example of double negation using “I am hungry”

“It is not true that I am not hungry” Implies that I am hungry

Use “⊥” in the negation rules to facilitate contradiction.

What does ⊥ mean?

⊥ means there is a contradiction.=

¬E → If we believe that a proposition is true and false, we have a contradiction.

⊥E → If we deduce a contradiction, we can conclude anything

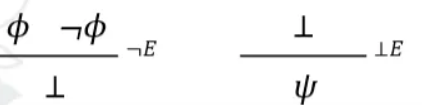
Define conditional introduction

→ If we assume that ϕ holds, and we prove ψ, then we know ϕ implies ψ

→ The box denotes a subproof, ϕ is a local premise and ψ is a local conclusion.

→ “Let us say that ϕ, then from this we can conclude ψ”

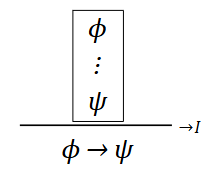
Argue that Q ⊢ P → (Q ∧ P) using subproofs

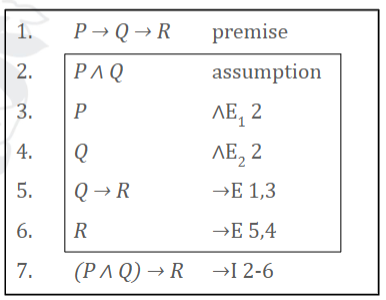
Let us argue that: P → Q → R ⊢ (P ∧ Q) → R using conditional & conjunction

Define biconditional reasoning

→ Conceptually, biconditional ϕ ↔ ψ is equivalent to (ϕ → ψ) ∧ (ψ → ϕ)

→ ↔ E_i is the biconditional modus ponens law, but it is symmetric

→ We can introduce a biconditional with 2 subproofs.

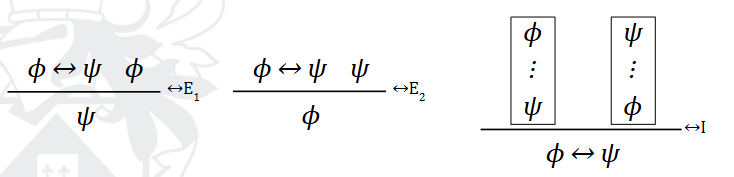
Define negation introduction

→ If we assume that ϕ holds, and can deduce a contradiction ⊥, then ϕ is false.

→ Reduction and absurdum

→ The assumption ϕ leads to absurdity, so it cannot be true.

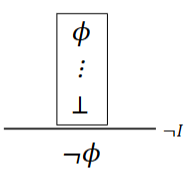
Define disjunction elimination

→ Proof by case analysis: we need to check for both cases of the disjunction.

→ We do not know which of ϕ or ψ holds.

→ If we know ϕ or ψ, and can derive χ from both, then χ is true.

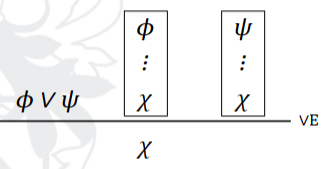
Use disjunction elimination to show ¬D where L v R and L v R can be telling the truth or lying

“L ∨ R. If L is lying then ¬D. If R is lying then ¬D. Therefore, ¬D.”

Derive modus tollens

What are the 4 De Morgans laws

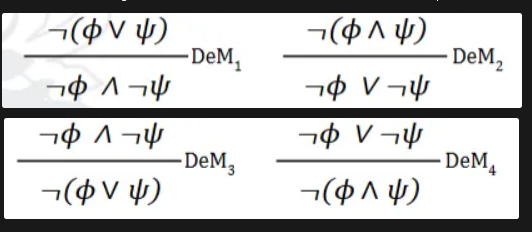
Show proof by contradiction as a natural reduction

Assuming ϕ is false leads to a contradiction, ϕ is true

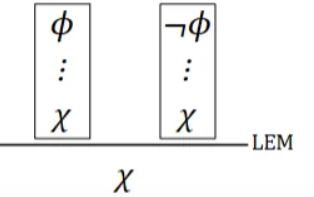
Show middle exlcusion as a natural reduction rule 

Every proposition ϕ is either true or false

Define Biconditional Modus Tollens (BMT)

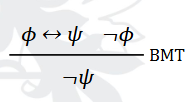
Define Biconditional De Morgans