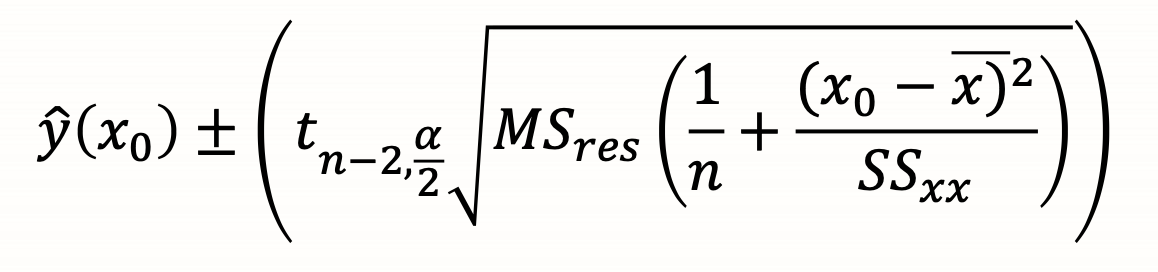data science

population

set of all possible observations of interest to problem at hand

sample

subset of population containing objects or outcomes that have actually been observed

parameter

describes a population (mean, standard deviation)

statistic

describes a sample

probability sampling

random selection

non probability

based on convenience

sampling with replacement

each data unit in the population can reappear in the sample

sampling without replacement

each data unit in population appears once in the sample

simple random sampling

equal chance

stratified 

divide into homogenous groups, sample each

cluster

divide into heterogenous clusters then sample clusters

why sampling is important

generalise population

prevent bias

reduce computation cost

cross validation

a sampling technique used during assessment phase to assess how well the model generalises to unseen data

how a cross validation works

split into k fold

train on k-1 folds

validate on remaining folds

repeat k times

average performance

aspects of data quality

accuracy, completeness, consistency, timeliness, validity, uniqueness

variance

{(n-mean)² + (n1-mean)² …}/ n-1

standard deviation

square root of variance

histogram

displays the frequency with which values occur in data

Lq

n+3/4 if odd

n+2/4 if even

Q1

X(Lq) if lq is integer

{X(Lq-0.5)+X(Lq+0.5)} / 2 if Lq is not integer

Q3

If Lq is integer: X(n+1-Lq)

If Lq is not integer:

X{(n+1 - Lq - 0.5)+X(n+1-Lq+0.5)}/2

fences

step = 1.5(Q3-Q1)

UIF = Q3+step

LIF = Q1- step

Outlier formula

(>1.5XIQR from median)

what statistics to use on symmetrical data with no outliers

standard deviation, mean

what to use on skewed data

median, quartiles

sample space

set of all possible outcomes of an experiment

event

sub set of the sample space

product rule

P(A or C) = P(A+C)/P(C)

addition rule

P(A or C)=P(A)+P(C)-P(AandC)

system failure (mutually exclusive)

P(System fail)= P(b1)+P(b2)…

parallel systems(all components must fail)

P(system failure)= P(b1)*P(b2)…

probability density function(PDF)

shows where the variable is most or less likely to fal

cumulative distribution function

probability that the random variable is less than or equal to a certain value

binomial distribution

fixed number of trials
each trial has two possible outcomes

probability of success is equal for each trial

you are counting number of successes

uniform distribution

all outcomes are equally likely

can be discrete or continuous

e.g rolling a die

poisson distribution

measuring number of events that occur within time space or area

events occur independantly

average rate of occurrence is constant

exponential distribution

measuring the time or distance between events

events occur continuously and independently at a constant average rate

always positive values

binomial distribution mean and variance

mean= n*p

variance=n*p(1-p)

me=number of trials

p=probability of success in each trial

uniform distribution mean and variance

mean=(a+b)/2

variance = (b-a+1)²-1/12

if x is uniformly distributed between a and b variance=(b-a)²/12p

Poisson mean and variance

mean and variance = lambda

lambda = average number of events per intervalex

potential mean and variance

mean=1/lambda

variance=1/lambda²

lambda = events per unit time

normal distribution

continuous data

bell shaped curve

values cluster around meann

bayes theorem

P(A∣B)=P(BIA)P(A)/P(B)

probability plots

graphical tool to determine if a set of empirical observations comes from a population

compare CDF calculated for sampled values with the theoretical CDF

scatter plot is made to compare values

estimate the CDF from the data with n observations

F(xi)=P(X<=xi)=number of observations<=xi/n

sign test

non parametric

test for median of a random sample or median of the difference of two random samples

nu

null hypothesis

assumption is correct

p<=0.05

reject null hypothesisp

p>0.05

fail to reject

issues with a small sample

central limit theorem does not apply

standard deviation of the sample is not a good approximation of population standard deviation

solution to small sample size (parametric analysis)

if population is approximately normal, calculation of confidence intervals can be performed using student t distribution

student t distribution

tn-1= √n(X-u)/s

for a 2 sided confidence interval the confidence interval length L=

L=2(tn-1,a/2)s/√n

simple regression model

yi=Bo+B1Xi+Ei

yi=observations of dependent variable

xi= observations of independent

Ei= term error

Bo=y-intercept B1 is slope of true model

how to find one of best fit

using calculus solution is

b1=SSxy/SSxx

b0=ȳ-b1x̄

x̄ and ȳ are sample means

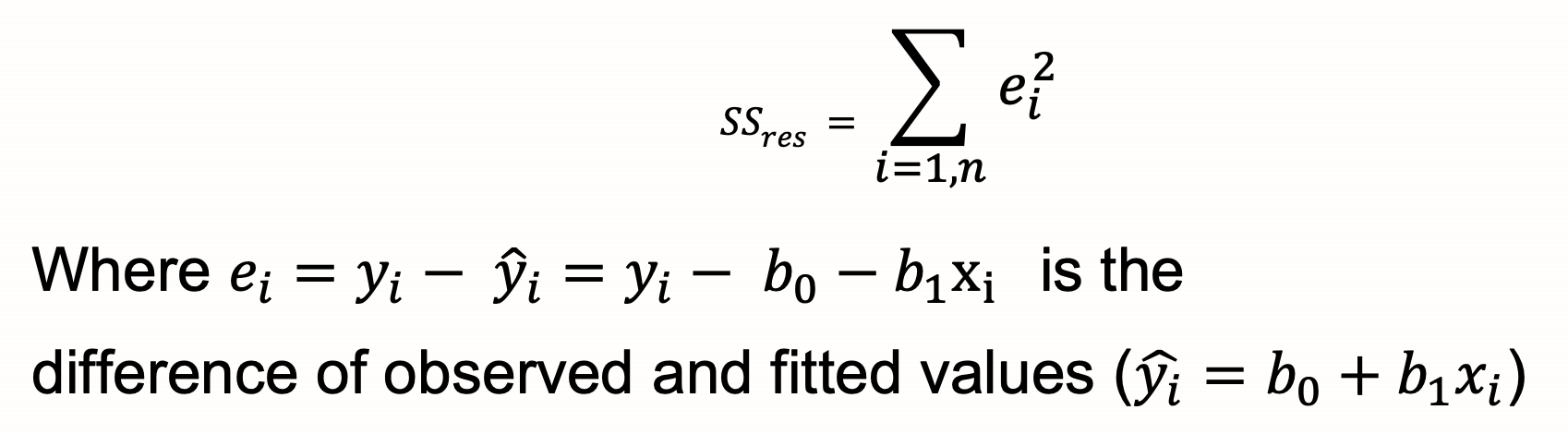
SSxx and SSxy

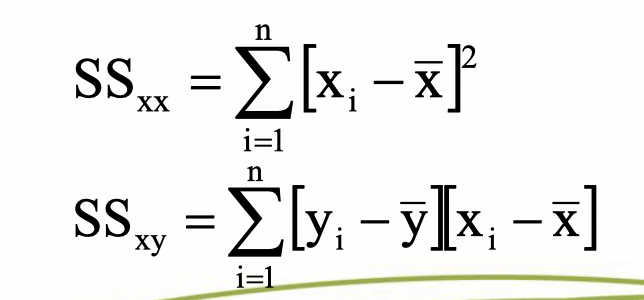
how to measure error

residual error

mean squared error MSres

SSres/n-k

n=error degrees of freedom

k=pairs of observations

SStot (total sum of squares)

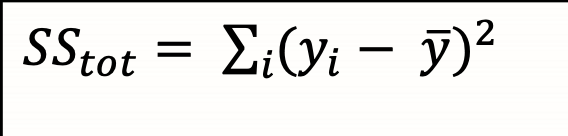
SSreg (Regression sum of squares)

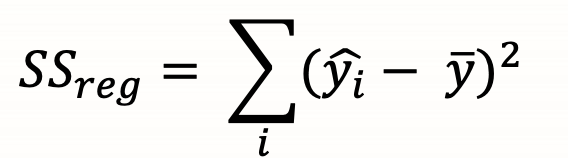
SSres (sum of squared residuals)

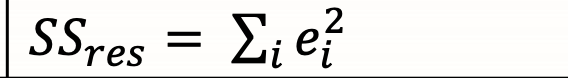
R²(Proportion of total variation in y accounted for by regression line)

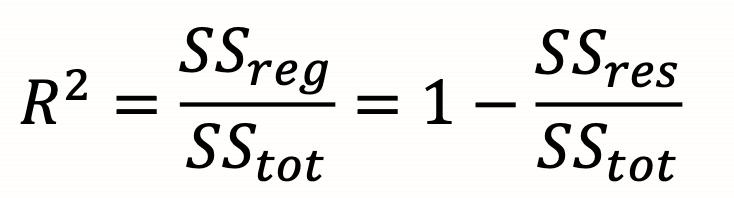
Goodness of fit statistics-adjusted coefficient of determination

Distributions of parameters

provided the residuals are normally distributed N(0,sigma²) the standard deviations are

confidence intervals of parameters Bo B1

distributions of parameters B0 B1

confidence intervals of regression line