Linear Algebra

solution set

Set of vectors that satisfy a condition

if W is a subspace in Rⁿ ,

• W^⟂ is also a subspace of Rⁿ

• (W^⟂)^⟂ = W

• dim(W) + dim W^⟂ = n

Row(A)^⊥=

Nul(A)

Nul(A)^⊥=

Row(A)

Col(A)^⊥=

Nul(A^T)

Nul(A^T)^⊥=

Col(A)

when 2 vec orthogonal

when the dot product of 2 vect is 0

if A is n x n, then the geometric multiplicity is alway…

less than or equal to the algebraic multiplicity

if A is n x n, then the Algebraic multiplicity is alway…

more than or equal to the geometric multiplicity

Characteristic polynomial equation

f(λ)=

det(A- λI) or

λ2−Tr(A)λ+det(A) (best for large Matricies)

finding the inverse of any size matrix A

• write the matrix and then the standard basis vectors for the same dimension right next to it

• RREF the matrix, and mimic all the steps on the standard basis vector matrix
  

subspace of a matrix m x n

R^m

A matrix is invertible if

Det(A) != 0 aka matrix is 1-1 and onto

Properties of Projection Matrices

Let W be a subspace of Rn, define T:Rn→Rn by T(x)=xW, and let B be the standard matrix for T. Then:

1. Col(B)=W.

2. Nul(B)=W⊥.

3. B2=B.

4. If WA={0}, then 1 is an eigenvalue of B and the 1-eigenspace for B is W.

5. If WA=Rn, then 0 is an eigenvalue of B and the 0-eigenspace for B is W⊥.

6. B is similar to the diagonal matrix with m ones and n−m zeros on the diagonal, where m=dim(W).

Properties of Orthogonal Projections

Let W be a subspace of Rn, and define T:Rn→Rn by T(x)=xW. Then:

1. T is a linear transformation.

2. T(x)=x if and only if x is in W.

3. T(x)=0 if and only if x is in W⊥.

4. T◦T=T.

5. The range of T is W.

geometric multiplicity

dim(eigenspace), aka # of lin ind eigenvector

algebraic multiplicity

the amount of times the eigenval appears in a sol when sol for the characteristic polynomial

ex:

f(λ) = (λ + 3) (λ + 3)

λ has an algebraic multiplicity of 2 for the sol -3

Trace of a matrix

the sum of the diagonal entries of a matrix

rank Nullity theorem

for any consistent system of linear equations, (dim of column span)+(dim of solution set)=(number of variables).

nullity

dimension of the null space

column space

the span of the columns of a matrix

span

Homogeneous system

When b = 0 in Ax = b, if there is >1 sol, there are infinite sols.

vector equation

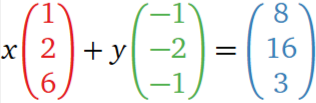
matrix equation

Ax = b

linearly independent

• There is a pivot in each column

• Ax = 0 is the only sol, has no free vars

Linear Dependents

• rows > col (m>n) and/or

• one of the vec in the set is a 0 vec

subspace

a subset of vectors that is:

• not empty

• closed under addition

• closed under scalar multiplication

null space

• the space containing the col of vectors (x in Ax = b) that make b = 0

• are always subspaces

injective transformation (1-1)

transformation such that every y (point in the new transformed set) has at most 1 corresponding x from the untransformed set (T(x) = y)

Injective transformation (1-1) properties

• Each vector in V has at most ONE corresponding vector in W

  • There is one pivot in every column and row

• Not all vectors in W have to be a correspondent in V

• must have at least as many rows as columns: m >= n

• Sets must be linearly Independent

surjective (onto)

transformation where every point in the new transformation has at least 1 corresponding val in the old transformation

surjective (onto) properties

• range of A is in T (all points in T have to be connected to some A)

• Multiple Vs in A can be mapped to 1 point in T

• There is a pivot in every row

transformation no-no’s

• have a var being added to a const

• have one or more of the resulting vars be a const

• have one or more of the resulting vars be an absolute power

basis

• the min # of vectors needed to get the same span as the subspace

  • ex of subspaces: sol set, column space, etc

• the vectors in a basis are lin indep

• found by writing the parametric form of a matrix and/or by using a linear combination of the vectors found using parametric form

Co-domain

the subspace of the vectors after they are transformed

rank

The rank of a matrix A, written rank(A), is the dimension of the column space Col(A)

dimension

The # of linearly independent vectors in the basis of a matrix

ex: if the sol set of a matrix is a plane in a 3D space, the dim is 2

trivial solution

the 0 vector

:

“such that”

∃

“there exists”

Closed under addition

If u and v are in V, then u+v is also in V.

unique sol

there is only 1 x in Ax=b that gets u a specific b

Closed under scalar multiplication

• if u is in V, then uc, where c is any # in R¹, is also in V

• you can check this by multiplying a vector by a random real # and seeing if it is still in V

• if there is even one situation where the system is not closed under addition, then the whole system is not closed

Invertible matrix

a square matrix transformation that can be multiplied by another square matrix to get the identity matrix  

A matrix is invertible if:

• matrix is square

• A and B are commutable

commutable

the product of 2 matrices is the same no matter the order

invertible matrix theorem

All the following statements about the matrix transformation T(x)=Ax where T:Rⁿ → Rⁿ, are true 

1. A is invertible.

2. T is invertible.

3. Nul(A)={0}.

4. The columns of A are linearly independent.

5. The columns of A span Rⁿ.

6. Ax=b has a unique solution for each b in Rⁿ.

7. T is one-to-one and onto.

8. det(A) and det(T) ≠ 0