Linear Algebra New Material

A vector x is in W Perp if?

1.if and only if x is orthogonal to every vector in a set that

spans W.

2. W perp is a subspace of Rn

What is the orthogonal complement of Row(A) and Col(A)

What is the connection between their inner dot product and the angle # between the two line segments from the origin to the points identified with u and v?

Suppose y is a linear combination of an orthogonal basis. How to compute c1 without row reduction

y dot u1 / u1 dot u1 = c1

an orthogonal projection is a sum of what two components

y hat: scalar * vector u
z: vector orthogonal to u

orthogonal set of unit vectors

orthonormal set

An m n matrix U has orthonormal columns if

U^Transpose * U = I

Define v1 and v2 and v3 in the Gram-Schmidt Process

How to construct an orthonormal basis given vectors v1 and v2 

Define an nxn orthogonal matrix and a least squares solution to Ax=b

(a) Least-squares solution to Ax=b

Let A be an m×n matrix and b∈Rm. A least-squares solution to Ax=b is a vector x^∈Rn that minimizes the sum of squared errors

|b-Ax^| <= |b-Ax| for any x existing in R^n

---

(b) n×n orthogonal matrix

An n×n matrix Q is orthogonal if its columns are orthonormal vectors and Q = Q^-1 and Q*Q^T = I

y^, y and z formulas

Suppose A= QR, where Q is an m x n matrix with orthogonal columns and R is

an n x n matrix. Show that if the columns of A are linearly dependent, then R cannot be invertible.

what 3 statements are logically equivalent from least squares chapter?

least squares solution formula

A^T*Ax = A^T*b

Even if you have the number of linearly independent vectors, under what condition could the matrix not be a basis for R^_?

If it contains the zero vector

row operations and linear dependence relations between the columns and the rows facts

row operations don't preserve linear dependence relationships across the columns but they do preserve the linear dependence relation of the rows

determinant of cA

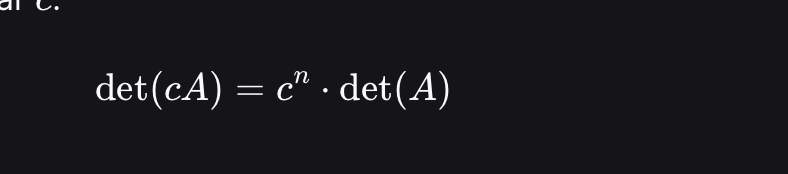
det(A^-1)

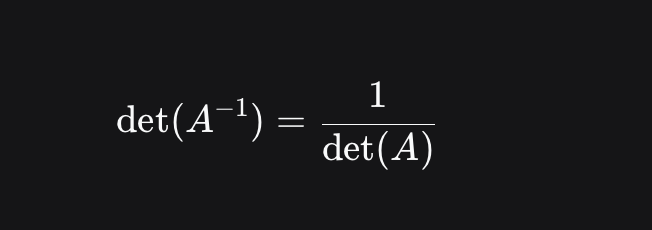
{u1 up through up} is an orthogonal basis for W, and y is in the span of W, the span{u1.up} then,

The projection of y onto W = y

The best approximation theorem

y^ is then called

the best approximation to y by elements of W.

Description of what it means for the error to be minimized

||y-v|| becomes ||y-y^||

By the Best Approximation Theorem, the distance from y to W is

||y-y^||

Relationship of orthogonally diagonalizable matrix to symmetric matrix

A is orthogonally diagonalizable if and only if it symmetric

Spectral theorem

The set of eigenvalues of a matrix A is called the spectrum of A.

-Let A be an nxn symmetric matrix.
1. A has n eigenvalues

2. The dimension of the eigenspace is equal to the multiplicity of the root of the characteristic polynomial

3. Eigenspaces are mutually orthogonal

4. A is orthogonally diagonalizable

5. An orthonormal basis of eigenvectors for Rn

If u1 up through up is an orthonormal basis for a subspace W of Rn, then the projection of y onto W is equal to

U*U^T*y for all y in R^n

condition for A being factored into QR

A is m x n and has linearly independent columns

define linear transformation

In linear algebra, a transformation (often specifically a linear transformation) is a mapping between two vector spaces that preserves vector addition and scalar multiplication.

One-to-one injective transformation

A linear transformation T:Rn→Rm is one-to-one if each vector in the codomain (Rm) is the image of at most one vector in the domain (Rn)

Onto surjective transformation

A linear transformation T:Rn→Rm is one-to-one if each vector in the codomain (Rm) is the image of at least one vector in the domain (Rn)

Standard Matrix of a Linear Transformation

The matrix A such that T(x)=Ax. Its columns are T(e1),T(e2),...