MA1210 - I S - 2025

El límite de una función constante f(x)=k es…

Siempre ese valor constante k

El límite de una función elevada a la n se saca…

Normalmente y elevando ese resultado a la n al final

El límite de una función con raíz n se saca…

Normalmente y sacando la raíz n a ese resultado al final

El límite de una función con valor absoluto se saca…

Normalmente y sacando valor absoluto a ese resultado al final

Cuando hay sumas y/o restas, el límite…

Las separa, de modo que se calcula el límite a cada una por aparte y luego se suman y/o restan los resultados

Cuando hay constantes k multiplicando, el límite…

Las separa, de modo que se calcula el límite normalmente y luego ese resultado se multiplica por k

Cuando hay multiplicaciones, el límite…

Las separa, de modo que se calculan por aparte normal y luego se multiplican esos resultados.

Cuando hay divisiones, el límite…

Las separa, de modo que siempre y cuando el denominador no sea 0, se calculan por aparte y luego se dividen esos resultados.

Factorización por sustitución

1. Invoco a U
2. Le doy a X el valor de la flechita del límite y la igualo a U
3. Despejo a X para obtener el valor que voy a usar de U
4. Uso U en lugar de X en toda la función

1/OO

= 0

1/0

= OO

Tipos de forma indeterminada

1. 0/0

2. 0*OO

3. OO/OO

4. OO - OO

Cómo se resuelven indeterminaciones con OO en su mayoría

Con f.c. forzado

log_a(a)=

1

log_a(x)+log_a(y)=

log_a(xy)

log_a(x)-log_a(y)=

log_a(x/y)

log_a(x)=

log_b(x)/log_b(a)

log_a(x^n)=

nlog_a(x)

tan² x + 1 =

sec² x

1 + cot² x

csc² x

sen² x =

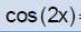
cos² x =

sen² (x/2) =

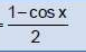
cos² (x/2) =

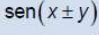
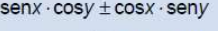
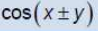
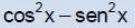
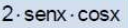
csc x =

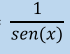
sec x =

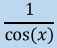
cot x =

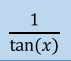
tan x =

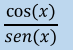
cot x =

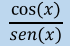
sen(-x) =

-sen x

cos (-x) =

cos x

tan (-x)

-tan x

cot (-x) =

-cot x

sec (-x) =

sec x

csc (-x) =

-csc x

Una fx es continua si

imagen de a = Límite de a, y ambos existen

Discontinuidad evitable

Si el límite existe, pero no da igual a la imagen de a o esta no existe

Discontinuidad INevitable

Si el límite no existe o da infinito

Si fx es derivable entonces

fx es continua

Si fx es continua entonces

no necesariamente fx es derivable

Si fx no es continua entonces

fx no es derivable

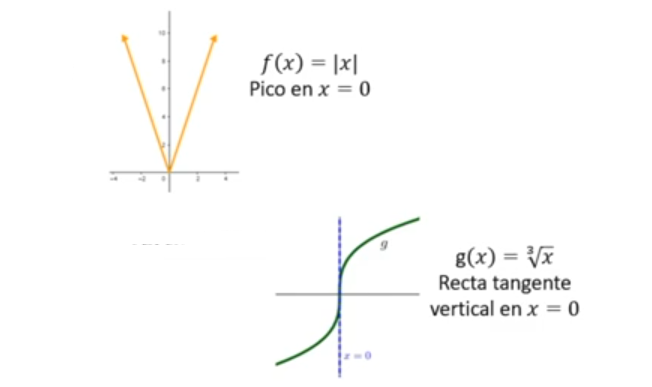
Casos donde una función continua no es derivable en a

-Si en a tiene una tangente vertical (raíz cúbica)

-Si en a tiene un pico (valor absoluto)

Derivada de k (constante)

= 0

Derivada de xⁿ

= n * x^n-1

Derivada de x

1

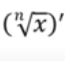
Derivada de…

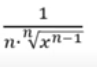
Derivada de…

Derivada de k * fx

k * f’x

Derivada de a^x

a^x * lna

Derivada de e^x

e^x

Derivada de log_ax

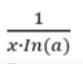
Derivada de lnx

1/x

Derivada de senx

cosx

Derivada de cosx

-senx

Derivada de tanx

sec²x

Derivada de secx

secx * tanx

Derivada de cscx

-cscx * cotx

Derivada de cotx

-csc²x

Derivada de arcsenx

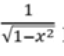
Derivada de arccosx

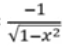
Derivada de arcsecx

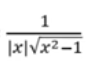
Derivada de arccscx

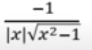
Derivada de arctanx

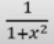
Derivada de arccotx

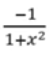
Derivada de fx +- gx

Derivada de fx +- Derivada de gx

Derivada de fx . gx

Derivada de fx . gx sin derivar + fx sin derivar . Derivada de gx

Derivada de fx sobre gx

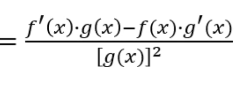
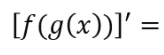
Regla de la cadena

Derivada de la función externa evaluada en la función interna . Derivada de la función interna

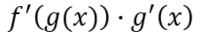
Cómo se calcula el dominio máximo de una función?

Para una función racional, se usa R- los ceros del denominador

Calcular intersección con el eje y

Se calcula f de 0

Se anota de segundo (0, el resultado)

Calcular intersección con el eje x

Igualar la función a cero (para funciones racionales)

Se anota de primero (el resultado, 0)

Calcular asíntotas verticales

Calculando límites laterales y que den algún infinito

Calcular asíntotas horizontales

Calculando límites al infinito y que den un número entero como c

Calcular asíntotas oblicuas

1. Calcular el lim al infinito de fx/x = m

2. Calcular el lim al infinito de fx-mx

3. Calcular el lim al infinito de fx -mx -b y que dé 0

O división de polinomios si el garriba-gabajo=1

Que dos asíntotas no puede tener una función a la vez

Oblicuas y horizontales

Si la primera derivada es mayor que 0

F es creciente

Si la primera derivada es menor que 0

F es decreciente

Si la primera derivada es igual a 0

F es constante

Si el número crítico c cambia de - a +

F en c es el mínimo relativo

Si el número crítico c cambia de + a -

F en c es el máximo relativo

Calcular números críticos

• Encontrar las restricciones metiendo el denominador de la primera derivada igualado a 0 en la calcu

• Igualar la primera derivada a 0 y calculando cada término por separado

Cómo hacer la tabla de signos para la primera derivada?

Poniendo los números críticos arriba de -OO a +OO

Poniendo cada parte de la derivada (cada factor que esté multiplicando), f' prima de x y fx al lado

Calcular el signo de las partes de la derivada, hacer ley de signos para f prima y anotando monotonía en fx

Cómo calcular los extremos relativos

Calculando la fx de los número críticos y escogiendo al mayor y menor

Ese resultado va de segundo, el número crítico de primero (c, resultado)

Si la segunda derivada es mayor que 0

f es cóncava hacia arriba :)

Si la segunda derivada es menor que 0

F es cóncava hacia abajo :(

Calcular los candidatos a puntos de inflexión

• Restricciones del denominador de la 2da derivada, igualando a 0

• Igualar la segunda derivada a 0, calcular cada término por aparte

Calcular los puntos de inflexión

Descartar restricciones de entre los puntos de inflexión

Reemplazar el candidato en la f original

Anotar el resultado de segundo (candidato, resultado)