GEOMETRY REGENTS

bisector

a line that divides something into 2 equal parts

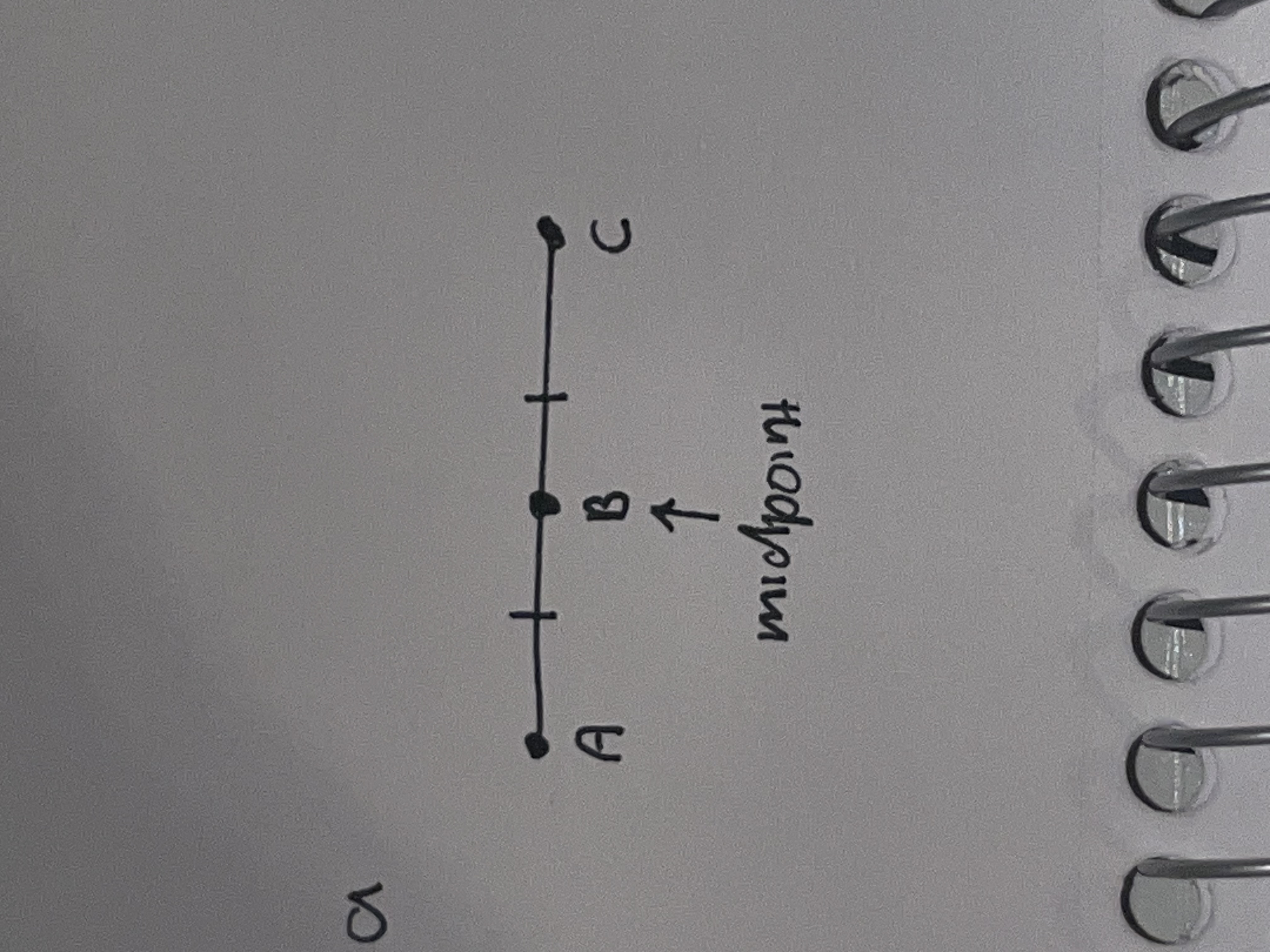
midpoint

Halfway between a line segment (congruent seg)

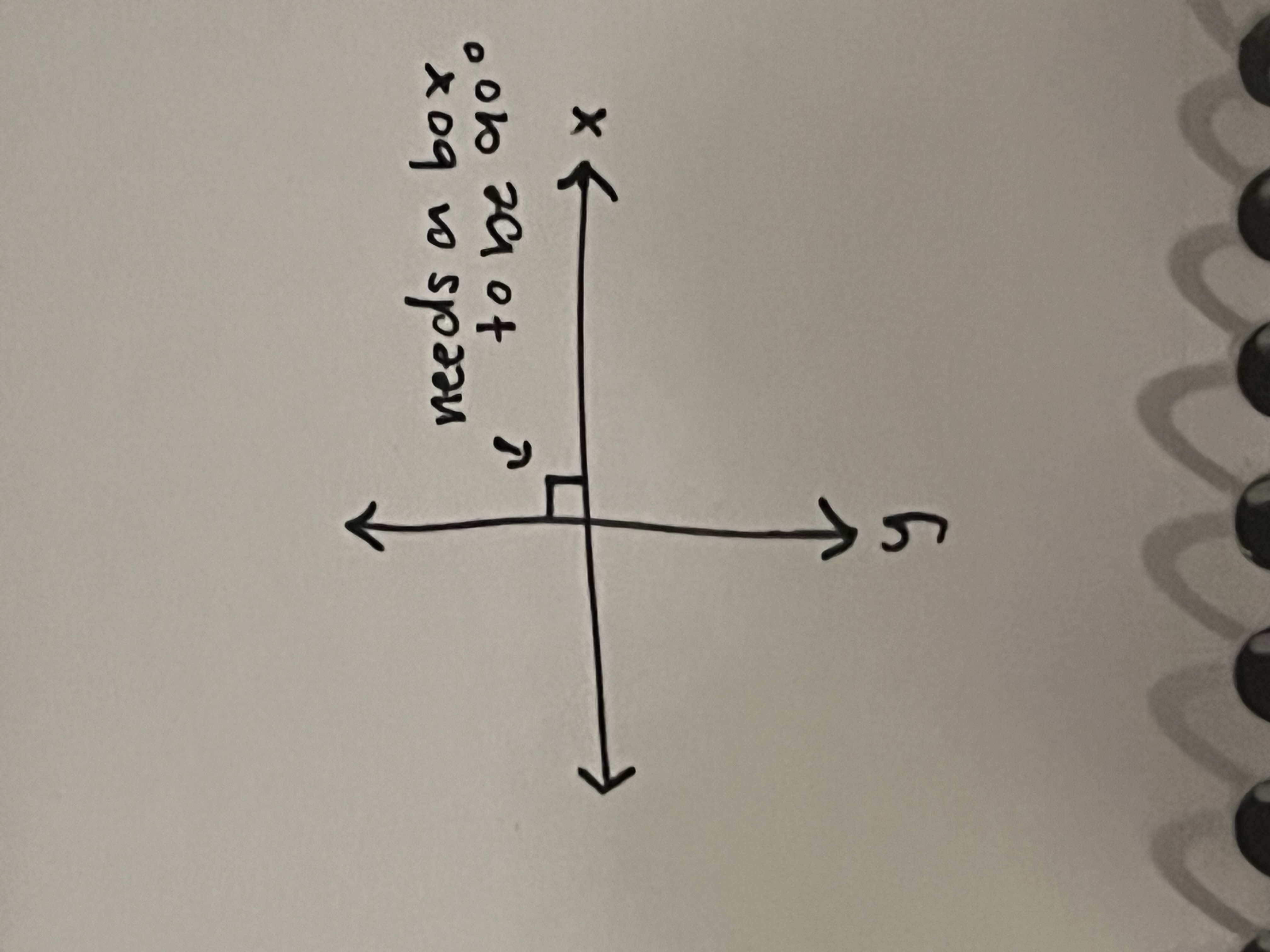
Perpendicular

Two lines that intersect at a 90* angle (right angle)

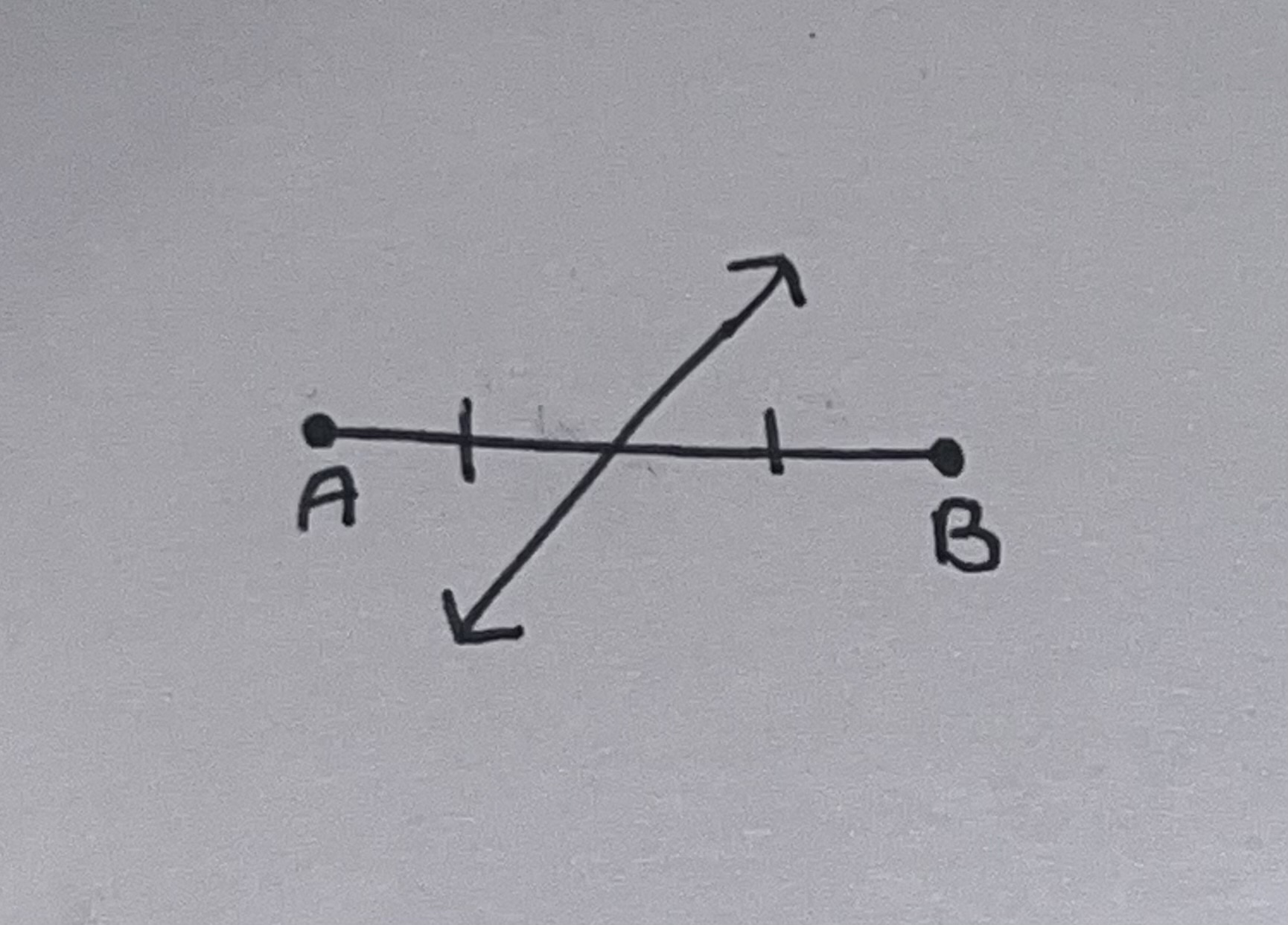
Segment bisector

A line segment or ray that intersects a segment at its midpoint

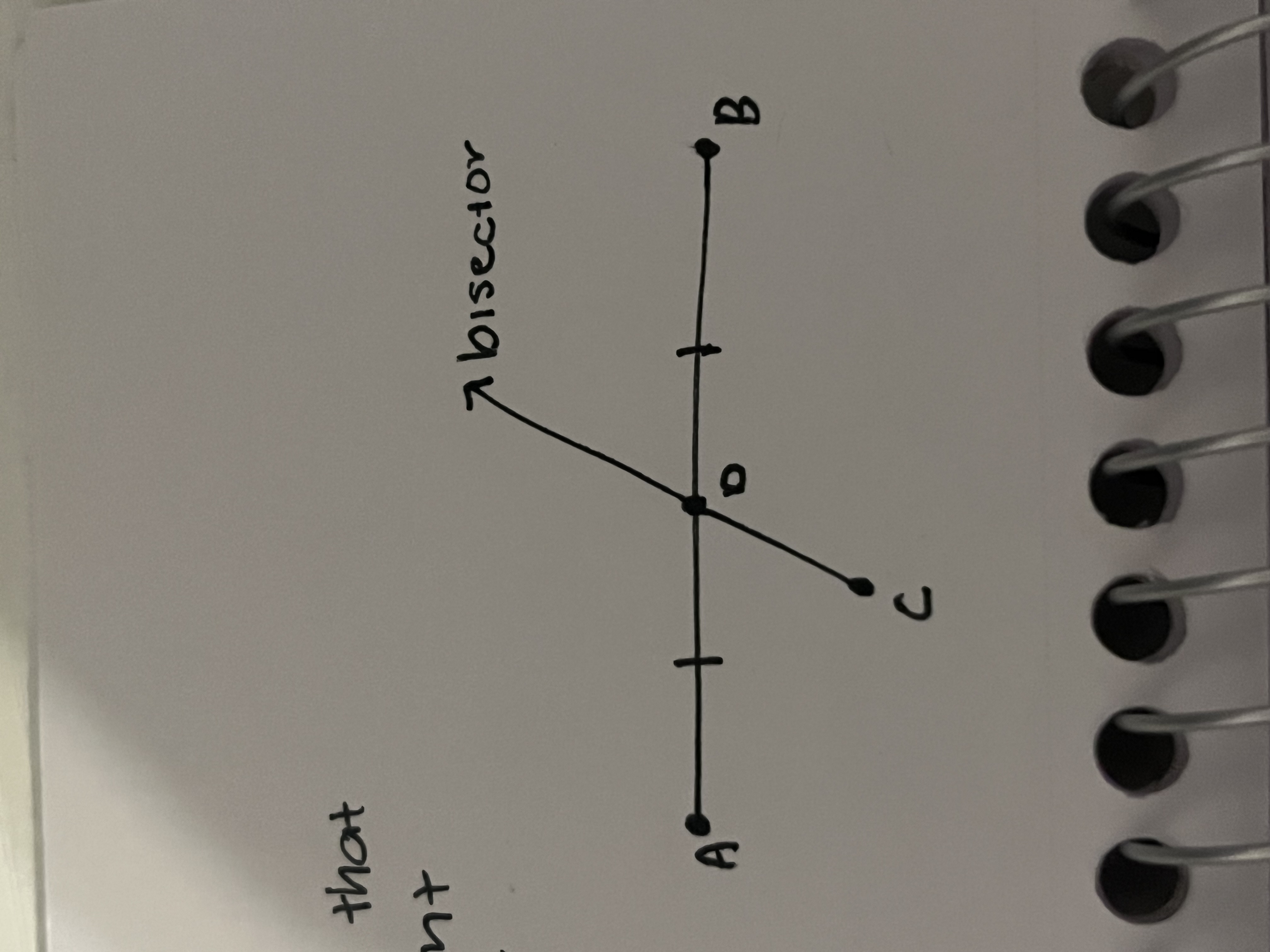
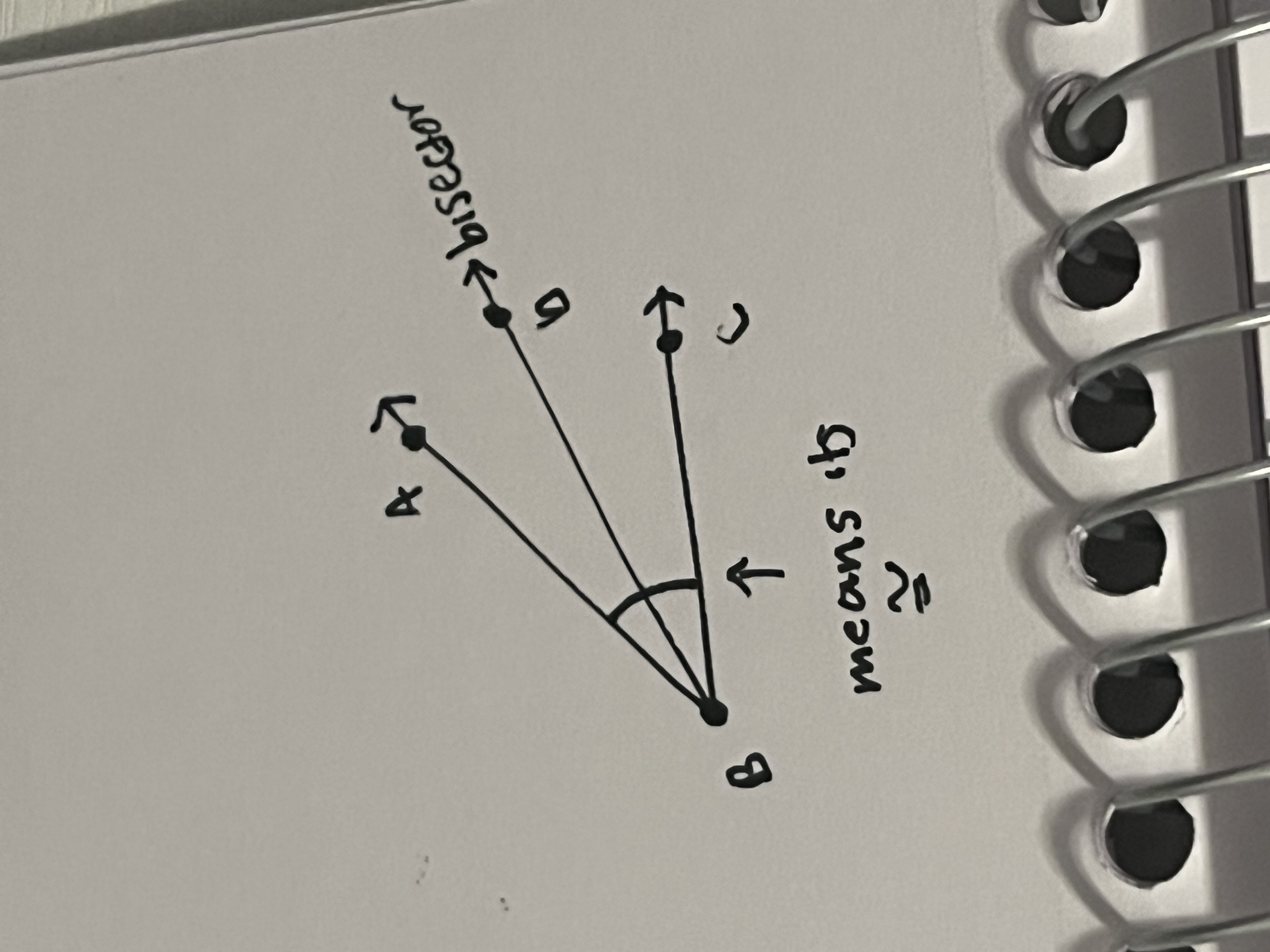
Angle bisector

A ray that divides an angle into 2 congruent angles

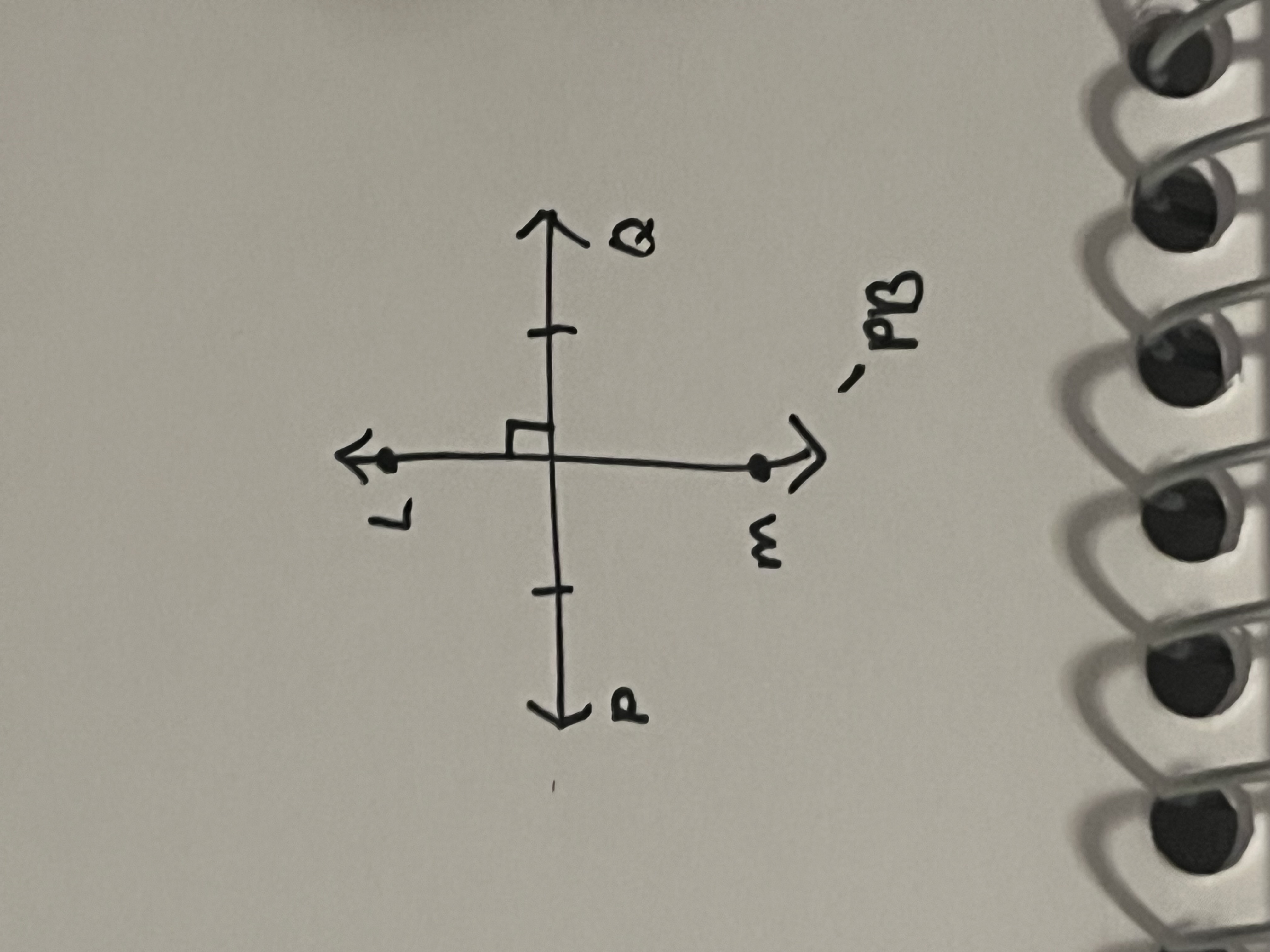
Perpendicular bisector

A line, segment, or ray perpendicular to a segment at its midpoint

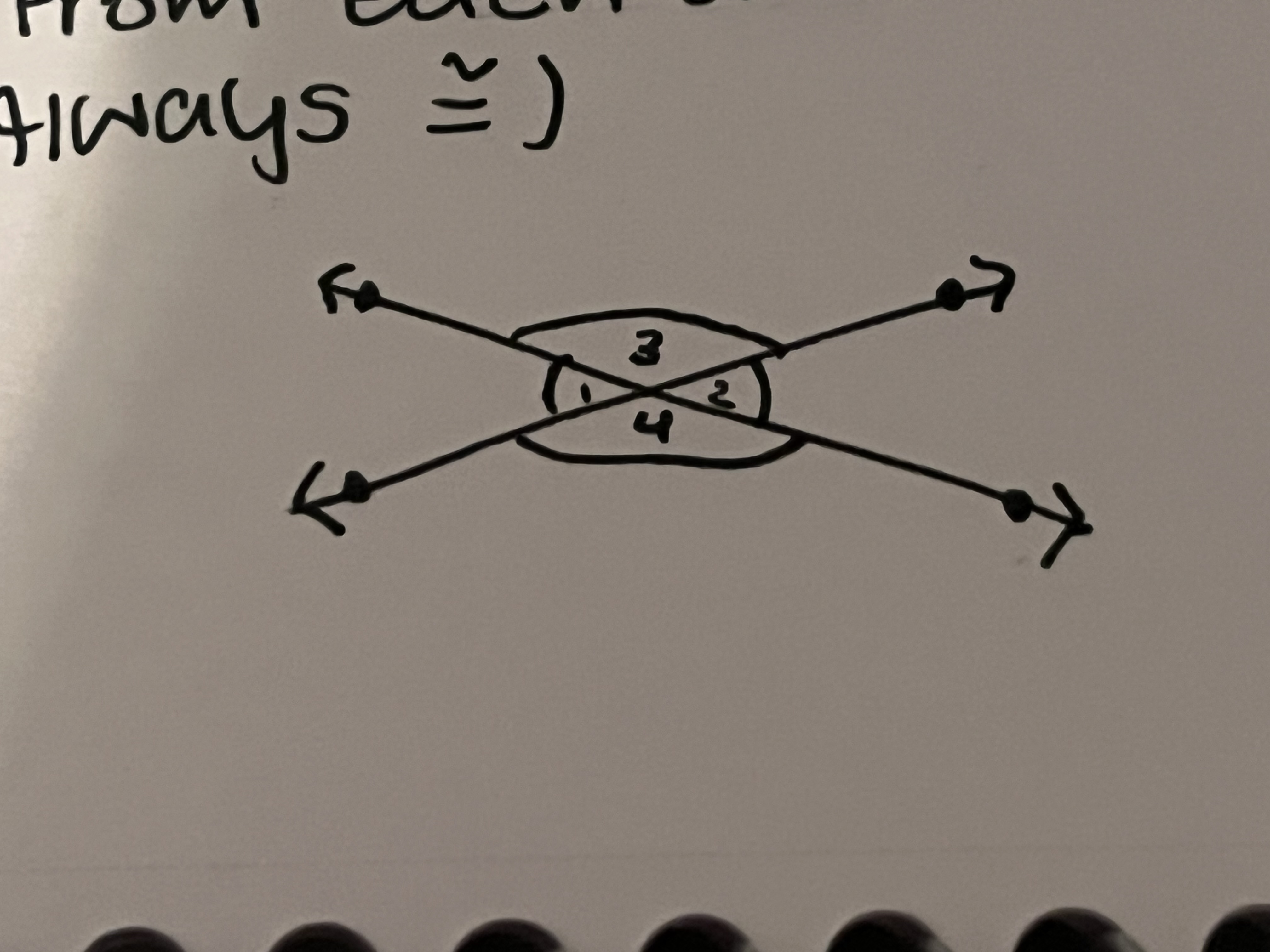
Vertical angles

2 angles directly across from each other on intersecting lines (always congruent)

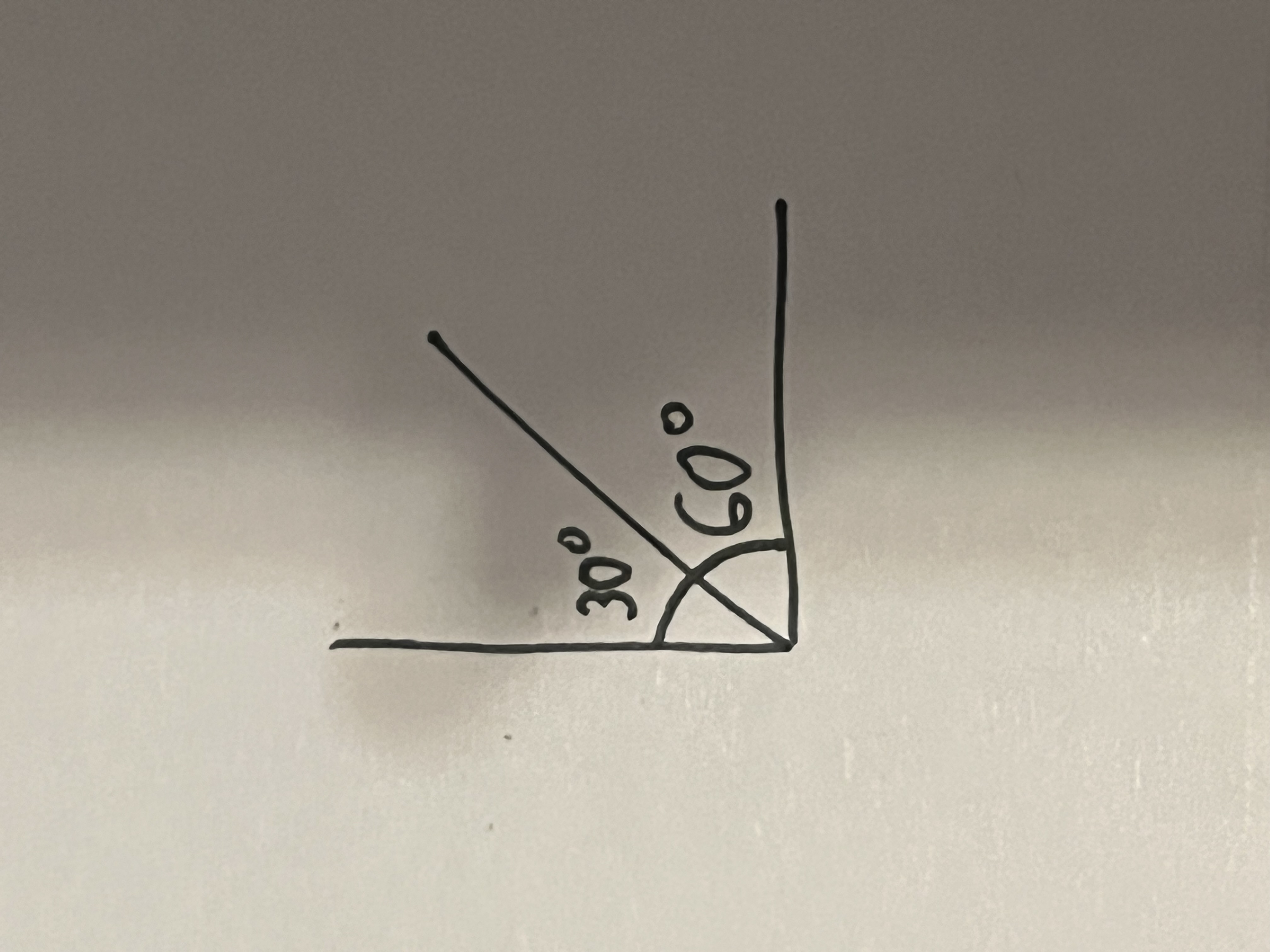
Complementary angles

Any 2 angles whose sum is 90*

supplementary angles

Any 2 angles whose sum is 180*

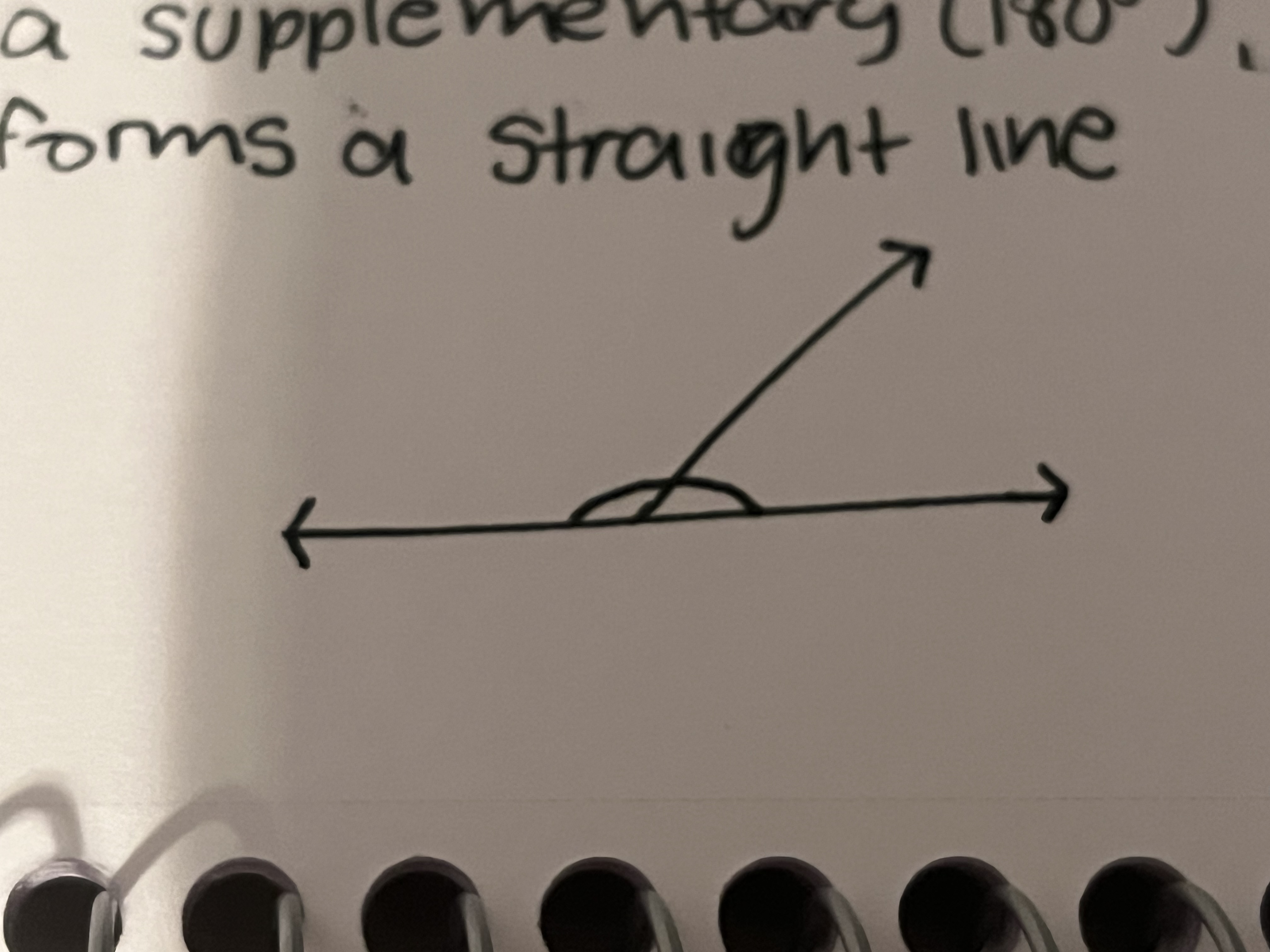
Linear angles

Two angles that are adjacent, supplementary (180*), forms a straight long

Distance formula

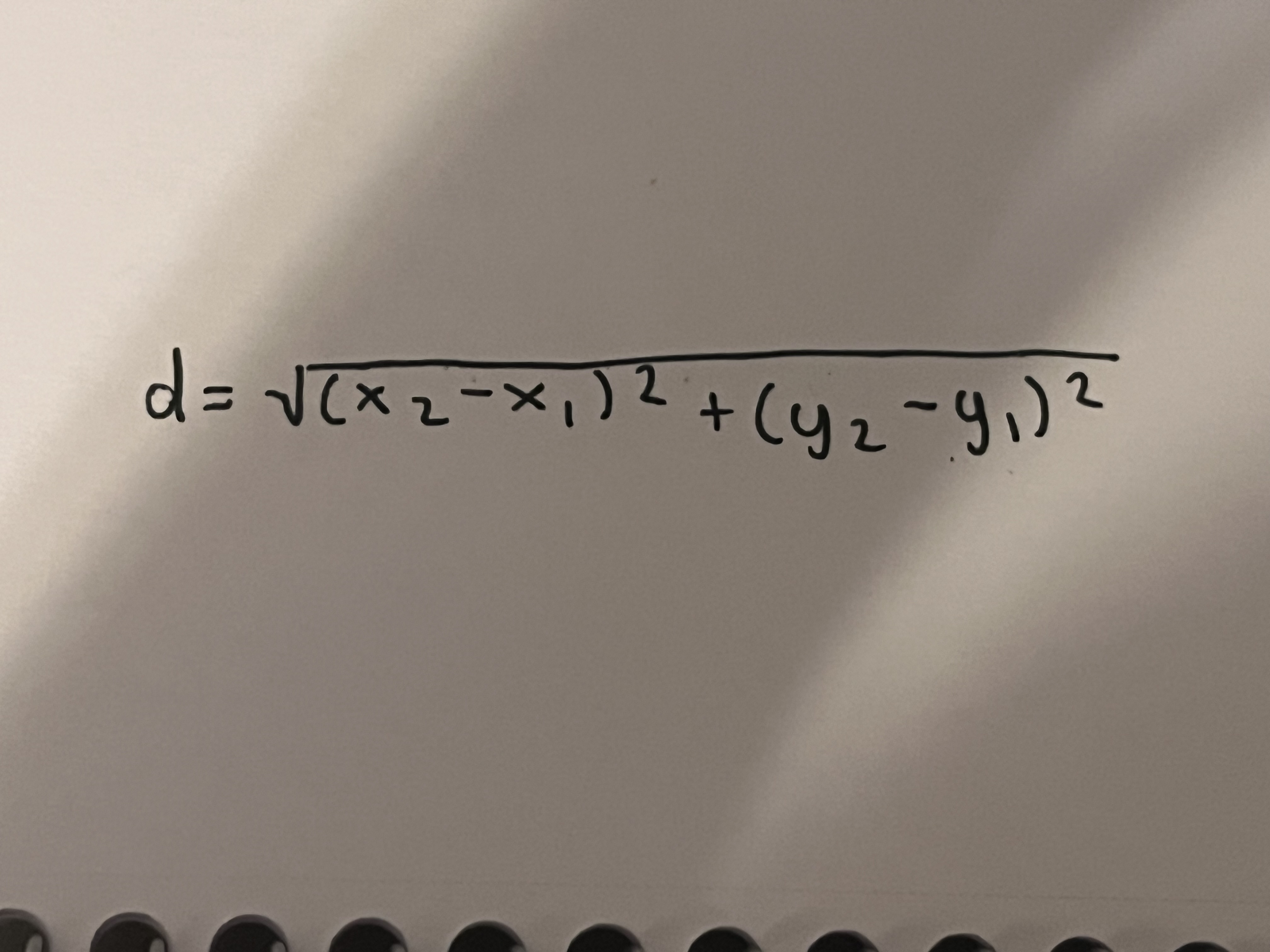
Midpoint formula

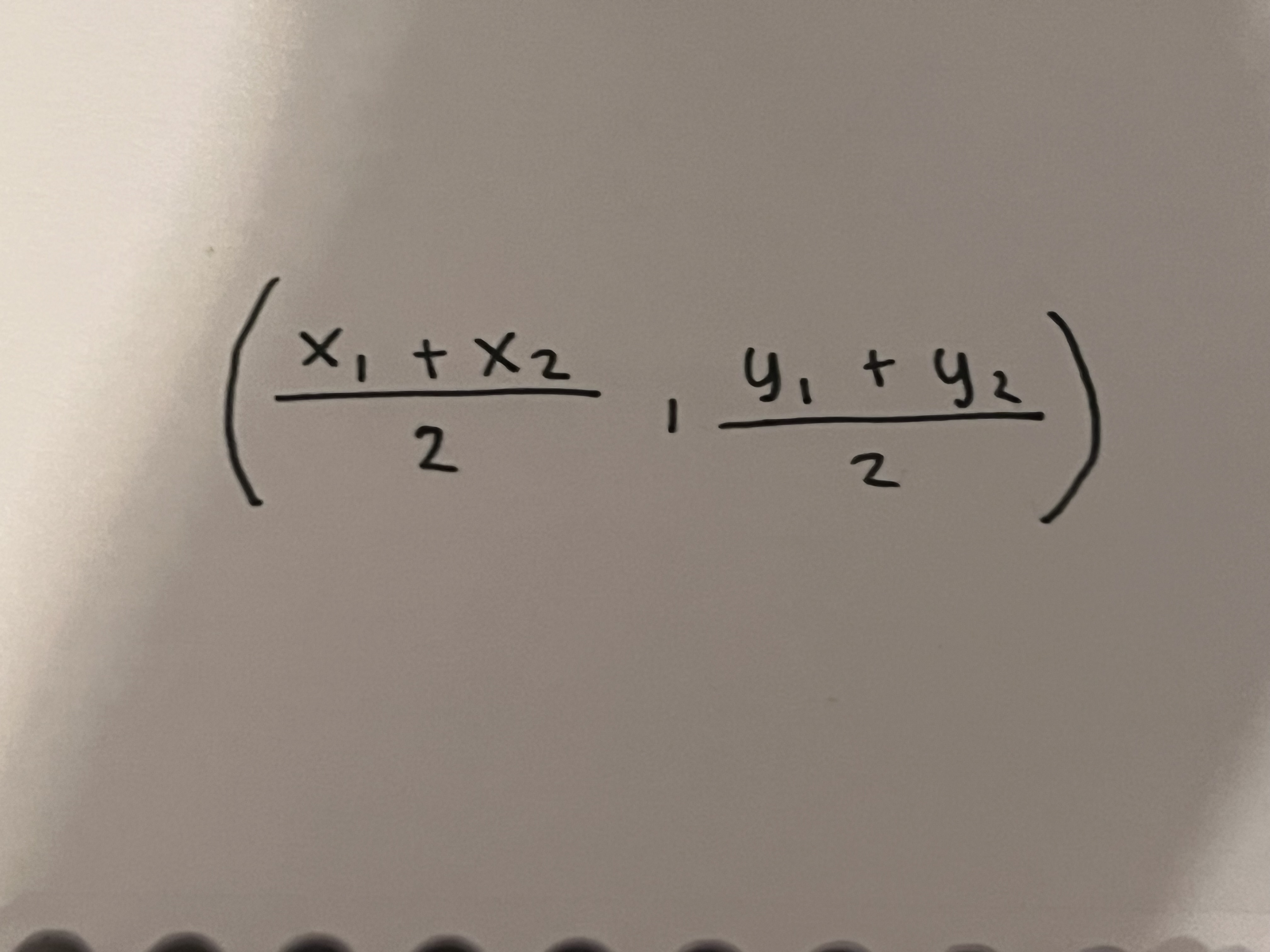
Slope formula

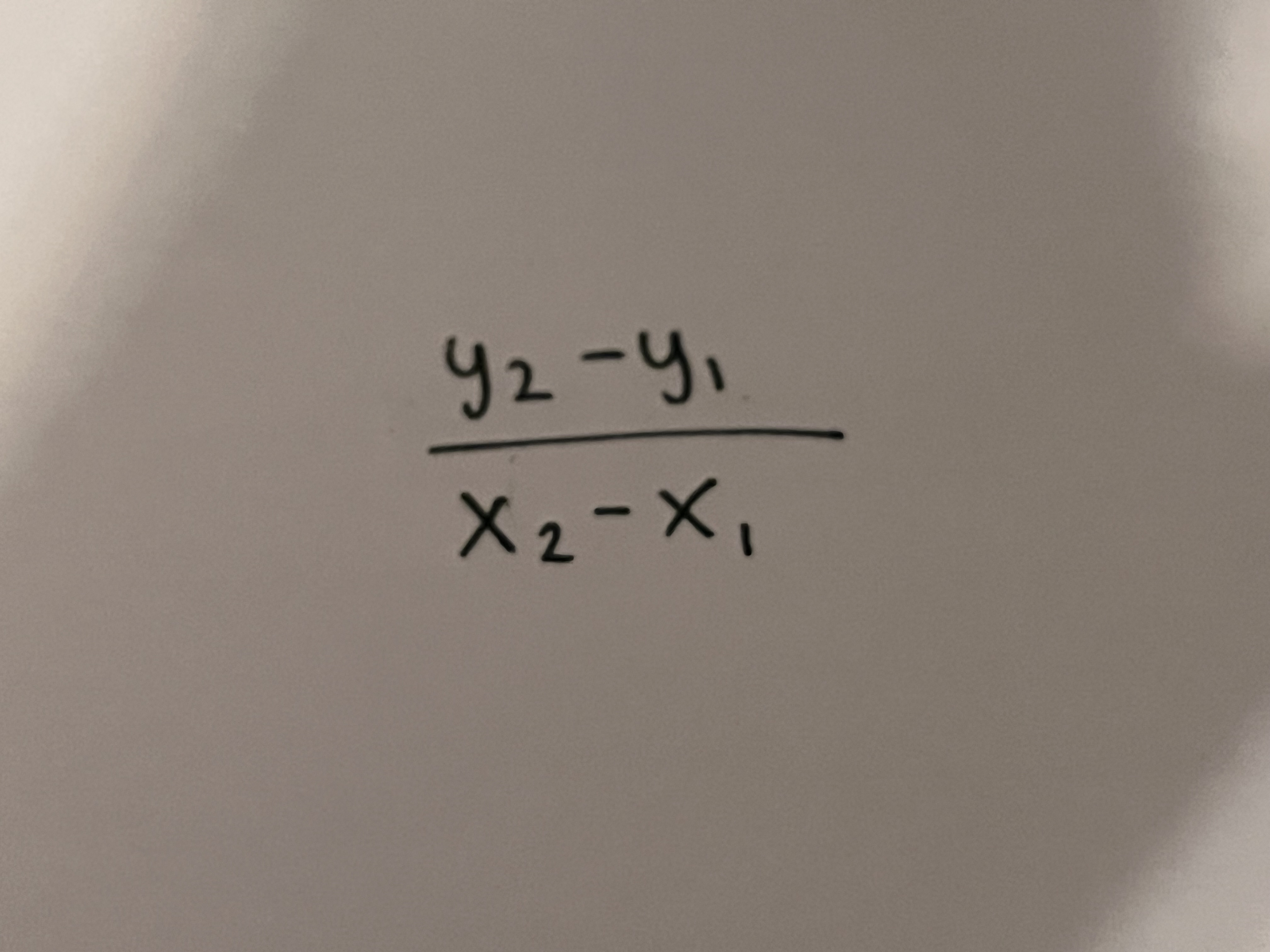
Rigid motion

A transformation that preserves size and shape (rotation, reflection, translation)

Translation

To vertically &/or horizontally slide a figure

Properties of translations

1- map lines to ll lines (true of transformations)

2- preserves angles (true of rigid motions)

3- preserves length/distance (true of rm)

Reflection

A flip over a line (line of reflection)

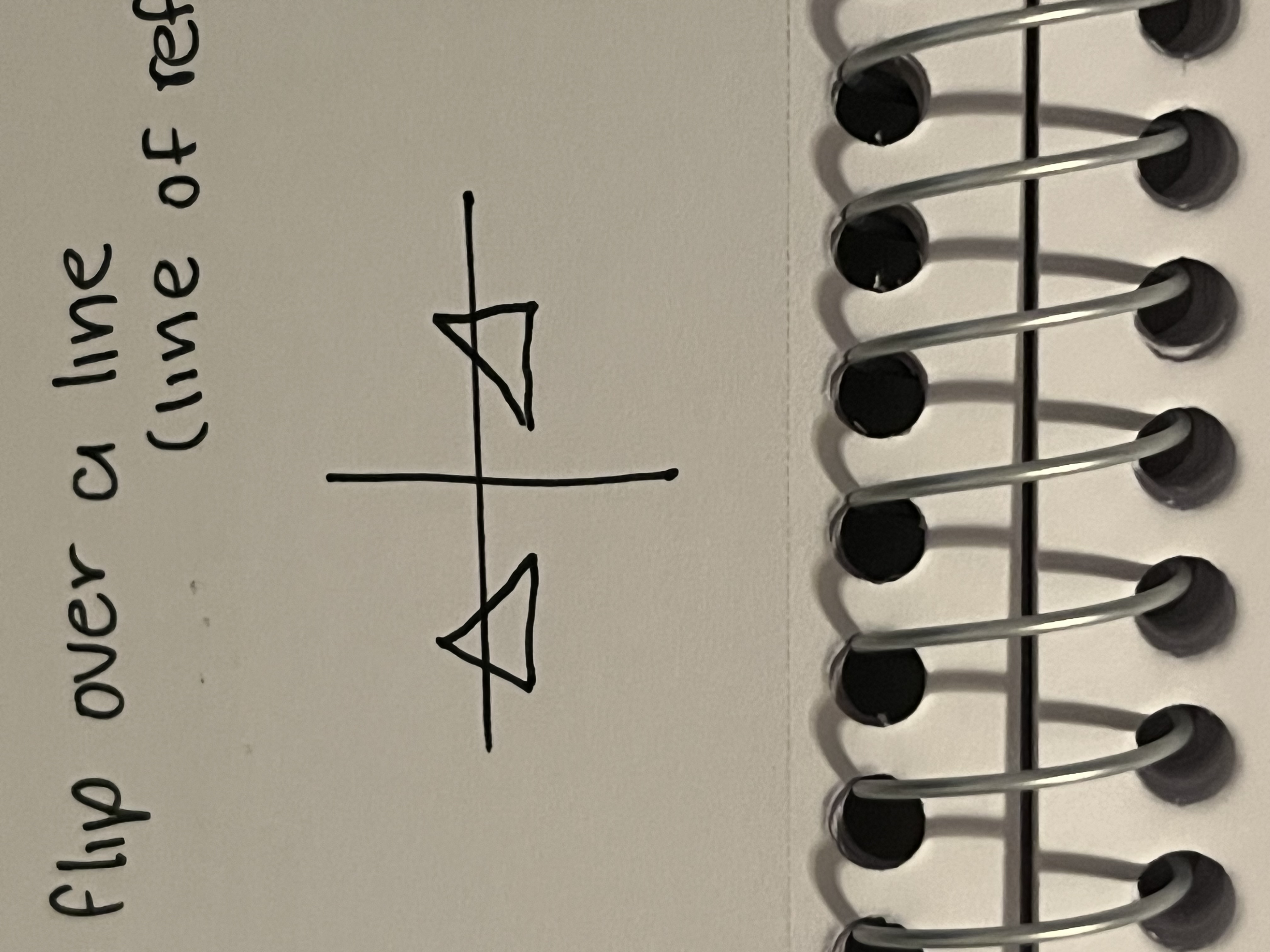
Reflection rule y=x

(x,y) → (y,x)

Reflection rule y=-x

(x,y) → (-y, -x)

Rotation rule 90* clockwise

(x,y) → (y,-x)

Rotation rule 90* counterclockwise

(x,y) → (-y,x)

Rotation rule 180*

(x,y) → (-x, y)

Rotation rule 270* clockwise

(x,y) → (-y, x)

Rotation rule 270* counterclockwise

(x,y) → (y, -x)

Median of a triangle

A line segment drawn from the vertex of a triangle to the midpoint of the opposite side

Altitude of a triangle

A line segment drawn from the vertex of a triangle such that it is perpendicular to the opposite

Area of a triangle

½ bh

Area of a circle

Pie r²

Circumference of a circle

2 pie r

Definition of parallelograms

A quadrilateral in which BOTH pairs of opposite sides are parallel

Properties of parallelograms

1- opp sides are congruent

2- opp sides are ll

3- opp angles are congruent

4- Consecutive (next to) angles are supp

5- diagonals bisect each other

Proving parallelograms in coordinate plane

Both pairs of opp sides are congruent (DISTANCE FORMULA OR Pythagorean theorem)

Both pairs of opposite sides sides are ll (SLOPE FORMULA)

One pair of OPP sides are congruent and ll (USE BOTH)

Properties of a rectangle

1- opp sides are congruent

2- opp sides are ll

3- opp angles are congruent

4- Consecutive (next to) angles are supp

5- diagonals bisect each other

6- all 4 angles are right angles

7- diagonals are congruent

Property of a rhombus

1- opp sides are congruent

2- opp sides are ll

3- opp angles are congruent

4- Consecutive (next to) angles are supp

5- diagonals bisect each other

6- all 4 sides are congruent

7- diagonals are perpendicular (90*)

8- diagonals bisect opp angles