Multivariable calculus lecture 13 & 14

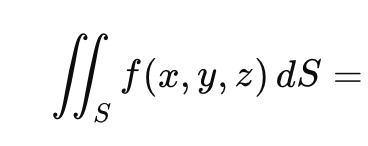
Surface integral of a scalar function

Graph surfaces like z=g(x,y)

1. parametrize using free variables

   1. eg. r(x,y) = ⟨x,y,g(x,y)⟩

2. dS = _______

3. integrate: _______

   1. 3 formulas (depending on how u define variables for surface)

4. SA = remove ___

“f”

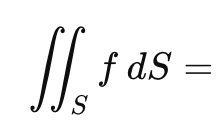
Surface integral of a scalar function

Case B: Surface given implicitly (not solvable for one variable)

1. General rule: _____

2. Sphere of x²+y²+z²=a²:

3. Cylinder of x²+y²=r²

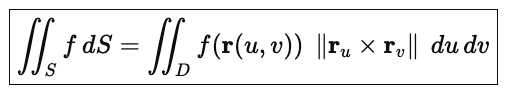
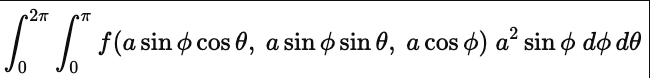
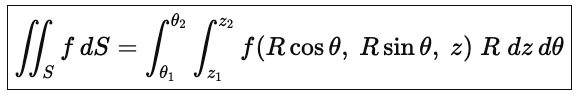
2 ways to parametrize surfaces

• if one variable is defined with other two variables (eg x=√(y²+z²)): make the other two variables __ and _

• if not (eg. x²=y²+z²), parametrize _____

u, v

one side

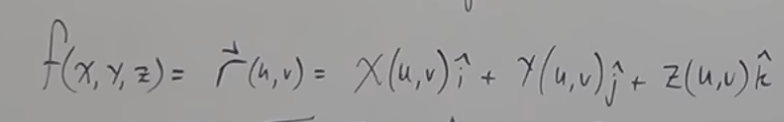
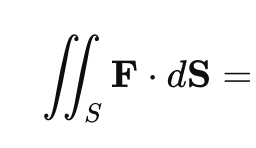
Flux Integrals / Surface Integrals of Vector Fields

For graph surfaces like z=g(x,y): F dot n = ______

orientation for normal is outward

if surfaces oriented in neg direction (downward, neg x or y direction): multiply negative 1 * normal vector

1. find integrand in terms of x&y

2. find region and integrate

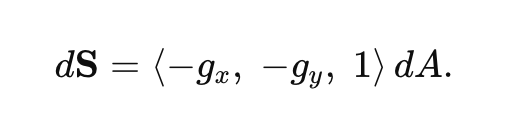
PQR dot picture above

Flux if S is a simple closed surface (like sphere): divergence theorem

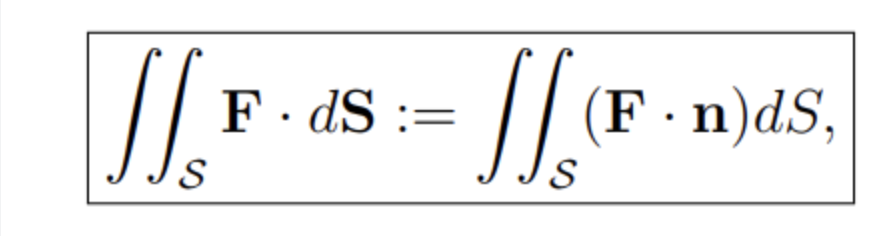
Flux Integrals / Surface Integrals of Vector Fields

For parametrically defined surfaces

for spheres

for cylinders

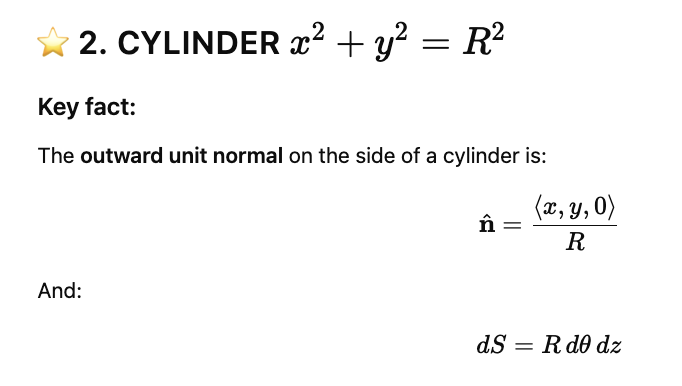
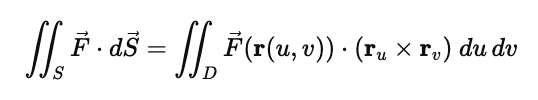
plane intercept form

x/a+y/b+z/c =1

Stoke’s theorem:

deals with line ∫ of simple closed curves over non-conservative vector fields ON ANY SURFACE

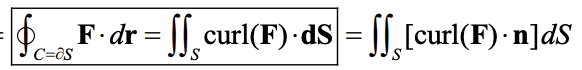
How to use stoke’s theorem

1. find ____

2. treat that as __ for a flux integral, find _ of surface and do dot product

3. find ___ and integrate

curlF, F, n, region

sphere volume

sphere SA

4/3πr³

4πr²