Circles (pt 2)

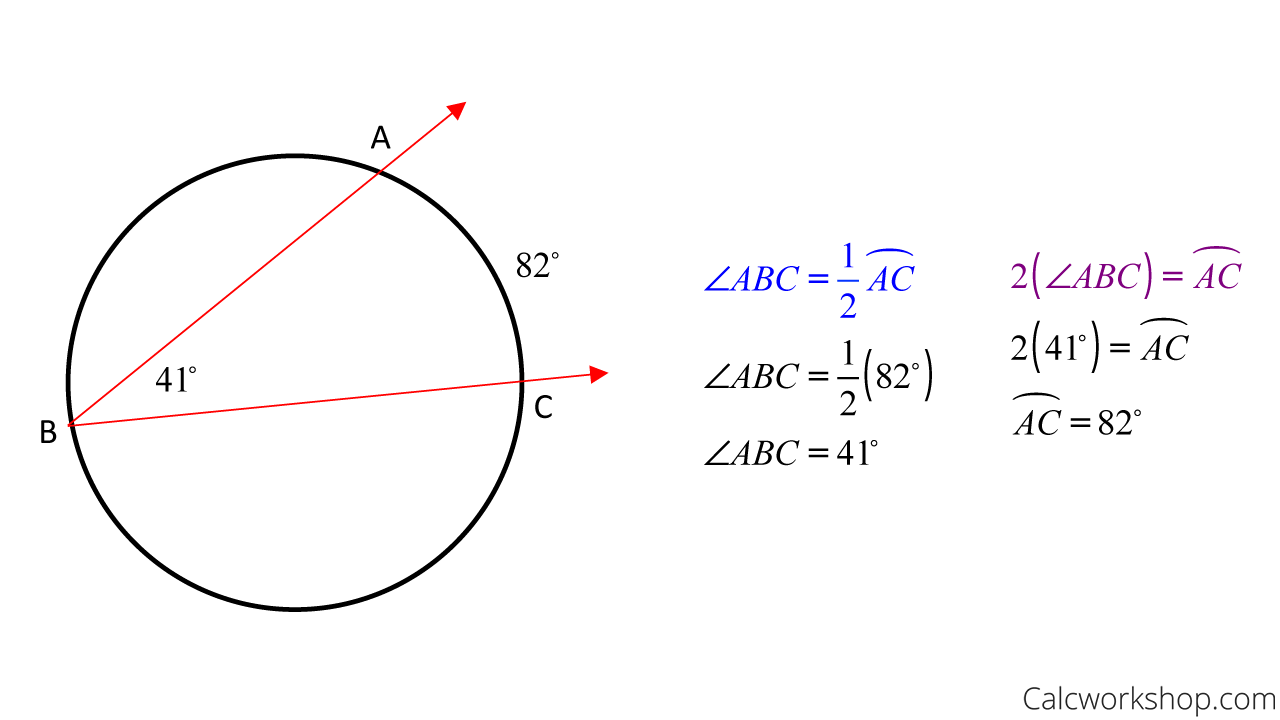
Inscribed Angle Theorem

If an angle is inscribed in a circle, then the measure of the inscribed angle is half the measure of the intercepted arc.

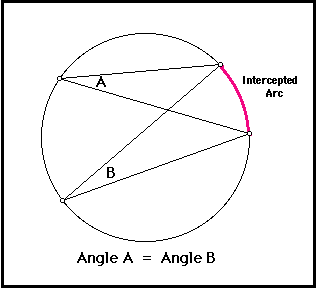
(If two inscribed angles share the same interpreted arc, they are congruent) AND THEREFORE

If two angles are inscribed in the same circle, then they are congruent.

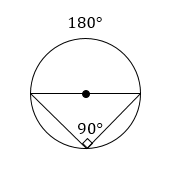
What is this?

If an angle is inscribed in a semicircle, it has a measure of 90 degrees

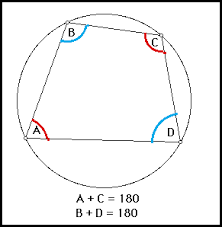
Inscribed Quadrilateral Theorem

If a quadrilateral is inscribed in a circle then its opposite angles are supplementary

Tanglent Line

Any Line that touches a circle exactly once (at one point)

Point of Tangency

Location where the circle and tangent line meet.

Common Tangent

Tangent line which is common in two or more circles.

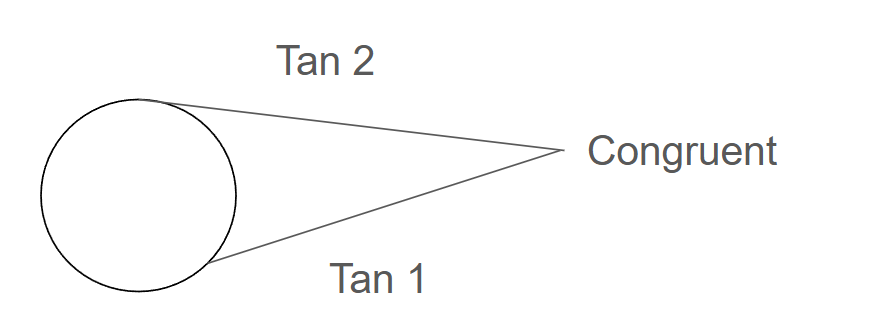
What is this?

If 2 tangents meet they’re congruent.

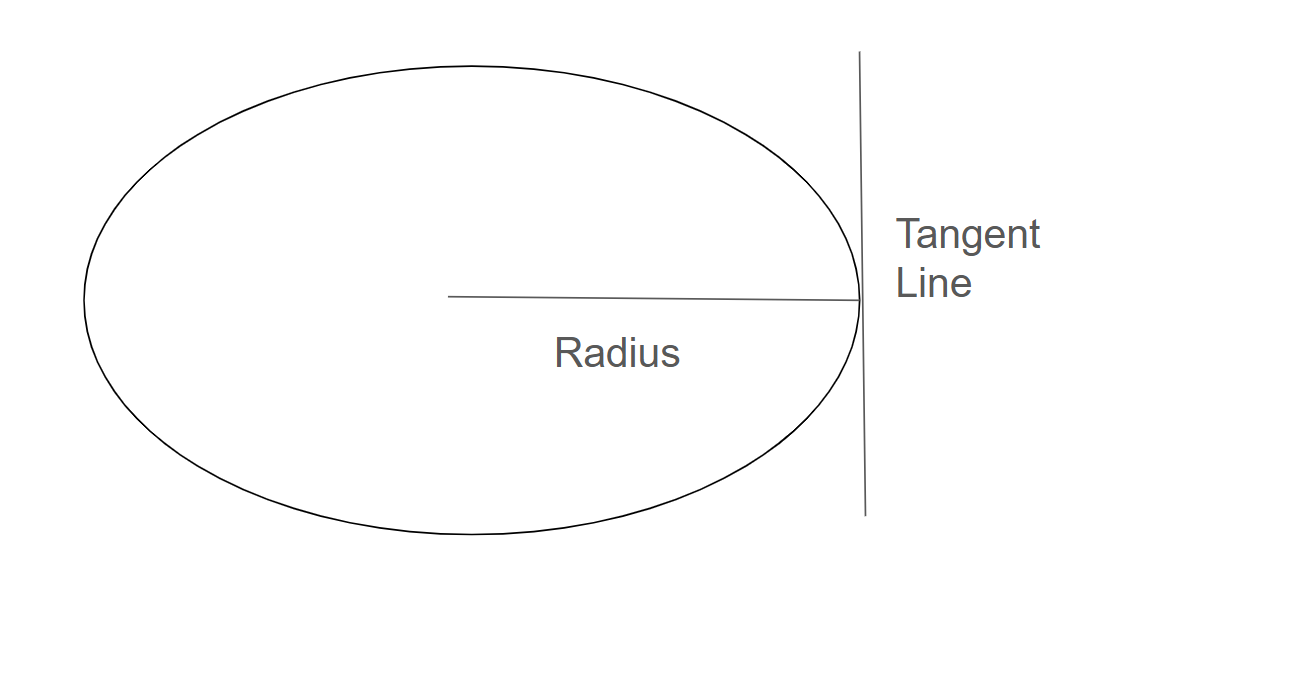
What is this?

If a tangent line and a radius meet they are perpendicular

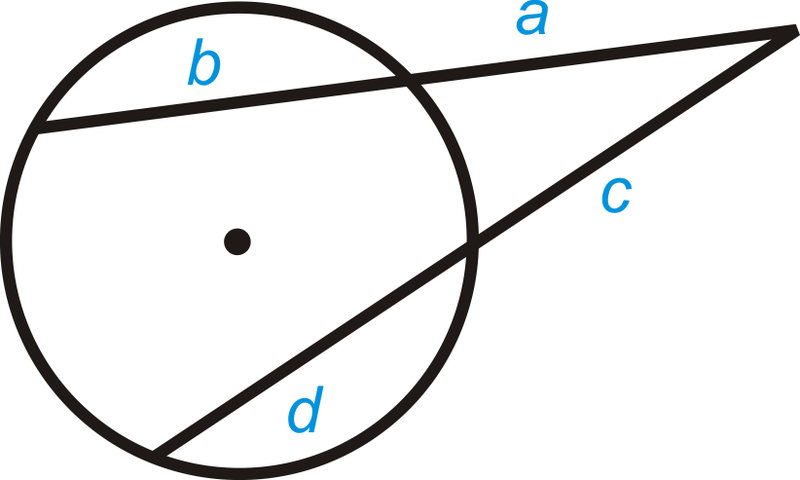
Formula when lines intersect outside the circle

Angle = (Big Arc - Small Arc)/2

For example, if angle = 5, and big arc = 15, small = 12

5 = (15-12)/2

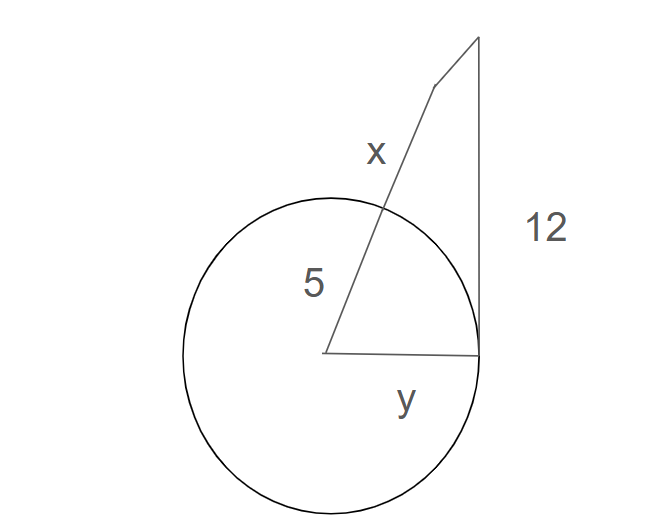
What is y and x?

y = 5: Because it’s also a radius. Using pythagorean theorem, we can find that 5² + 12² = c² leads C = 13. So 13-5 = 8. So X = 8.

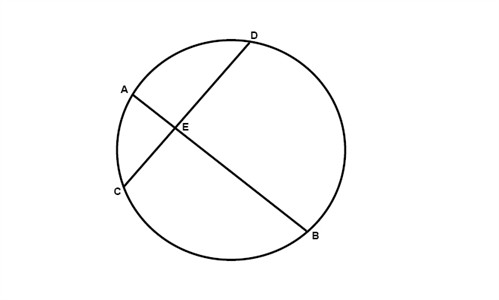
Formula when lines intersect inside the circle

Angle = (Big Arc + Small Arc)/2

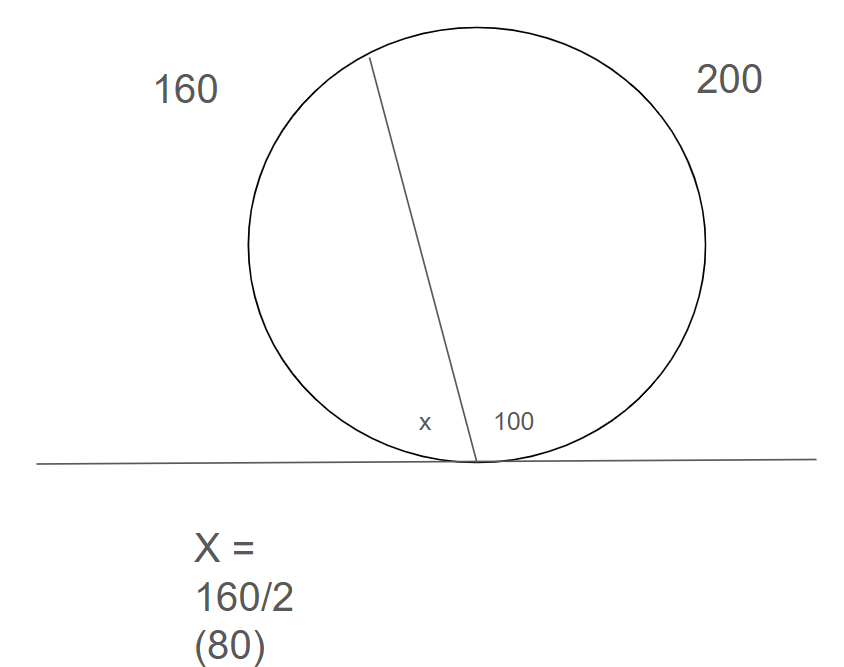
Formula when lines intersect on the circle

Angle = Arc/2

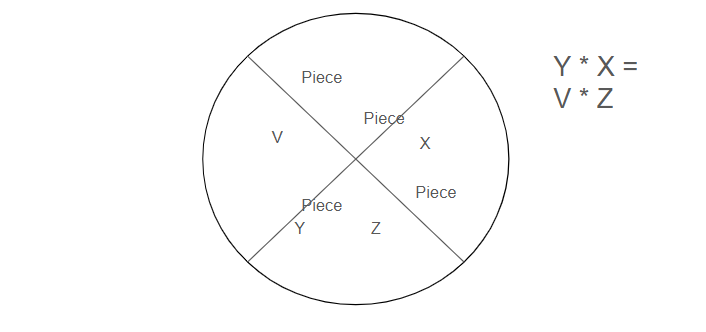
Intersecting chords/secants inside the circle

Piece * Piece = Piece * Piece

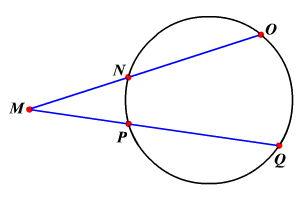
Intersecting secants outside the circle

Here, its MN (MO) Outside (Whole)

Outside (Whole) = Outside(Whole)

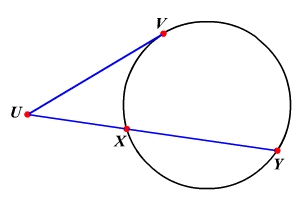
Intersecting secant and tangent outside the circle.

(Tangent)² = Outside (Whole)

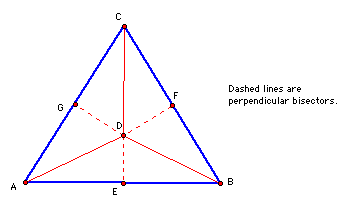
he point at which the three perpendicular bisectors of the sides of a triangle intersect and are all the same distance.

Where is the circumcenter if your triangle is obtuse?

Outside the circle.

Where is the circumcenter if your triangle is acute?

Inside the circle.

Where is the circumcenter if your triangle is a right triangle?

On the triangle

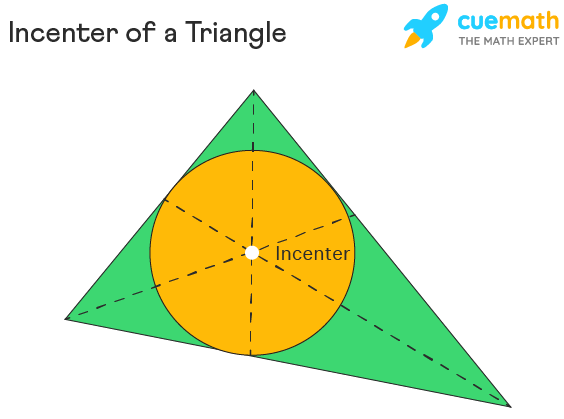
Incenter

the point where the three interior angle bisectors intersect located within the center of an inscribed circle.