Ch 3 enkelvoudige regressie

doel van lineaire regressie

verkrijgen van de best mogelijke voorspelling (conditionele verwachte waarde) van y gegeven de verklarende variabelen X1 ,,, Xp

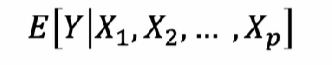
wanneer spreken we van een enkelvoudige lineaire regressie

indien we maar één verklarende variabele X in het model gebruiken

lineaire regressie : descriptieve aanpak

regressielijn door datapunten (x1, y1) , (xn, yn) die het best bij deze observaties past

lineaire regressie : inferentiële aanpak

veronderstelling dat de Y gegenereerd wordt als een lineaire combinatie van X en een foutterm Y = alpha + betaX + e

assumptie 0 (enkelvoudige lineaire regressie)

we veronderstellen voor onze datageneratieproces dat Y = alpha + beta X + e

de functie die X en Y verbindt is dus een

→ lineair in de parameters (non-lineaire transformaties zijn ok)

assumptie A1 en A2 enkelvoudige lineaire regressie

modelspecificatie

Y is de afhankelijke variabele, X de verklarende variabele en e de foutterm

A1 : E[e] = 0

A2 : de foutterm is onafhankelijk van X (dus E[e!X] = E[e])

combinatie A1 + A2 = E[e!X] = 0

→ X biedt geen informatie over de foutterm

onder A0, A1 en A2 is E[Y!X] een lineaire functie van X (bewijs)

→ voorspelling van Y

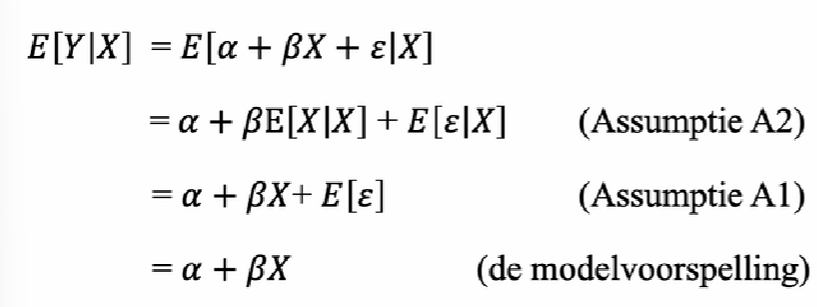
de verticale afstand van Y tov de punten op de rechte E[Y!X] is

de foutterm e= y-(alpha +betaX)

hoe noemen we alpha

de constante term / het intercept

hoe noemen we beta

de richtingscoefficient / hellingscoefficient

→ als X met een eenheid toeneemt, dan zal Y gemiddeld gezien met beta eenheden toenemen

assumptie A3

over het verband tussen de verschillende realisaties van het datageneralisatieproces

e1, e n zijn onderling onafhankelijk en volgen eenzelfde verdeling (iid)

(mogen geen invloed hebben op elkaar)

wat is een residu

een geschatte foutterm

ri = yi - ^a -^b Xi

de fouttermen zelf zijn onobserveerbaar, maar we kunnen het schatten aan de hand van de geschatte parameters alpa en beta

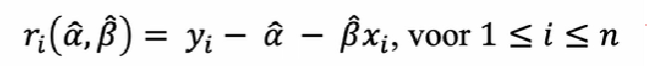
hoe kunnen A0,1,2,3 worden aanzien voor het datagenearieproces DGP

als een model (lineaire regressiemodel)

→ hiermee heb je een model gemaakt

kleinste kwadratenschatter OLS

we kiezen âlpha ^beta zodat de som van de gekwadrateerde aftsand tussen de observaties en de regressielijn zo klein mogelijk is

→ RSS residuals sum of squares

OLS schatters zijn dus de waardes die de RSS minimaliseren

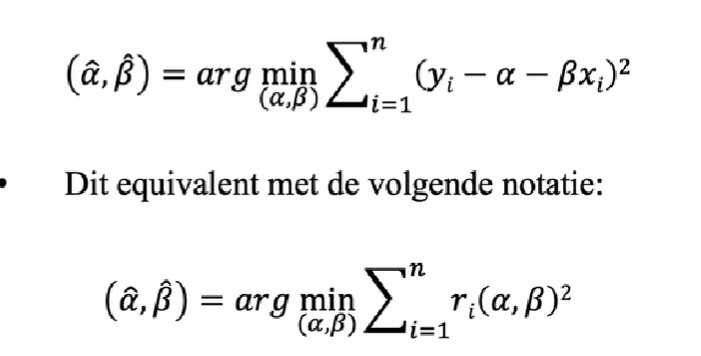
bepalen van alpha

waaraan is de som van de OLS residueen exact gelijk

aan 0

(door eerste orde afgeleiden van alpha)

→ per constructie is aan assumptie A1 voldaan (enkel zo indien er een interecept is)

bepalen van beta en welke eigenschap komt hier naar buiten

orthogonaliteit van de OLS residueen tegenover de verklarende variabelen (deels assumptie A2)

waaraan is beta gelijk (bij enkelvoudige regressie)

covariantie (X,Y) / Variantie (X)

is lineaire regressie symmetrisch

NEEEN

door het feit dat beta = covariantie van (X,Y) / Variantie (X)

wat is covariantie tussen X en Y

een maat voor de lineaire afhankelijkheid tussen twee kansvariabelen

meet in welke mate de ene variabele toeneemt/afneemt (bij pos/negatieve covariantie) als de andere variabele toeneemt

indien de covariantie gelijk is aan 0, impliceert dit lineaire onafhankelijkheid

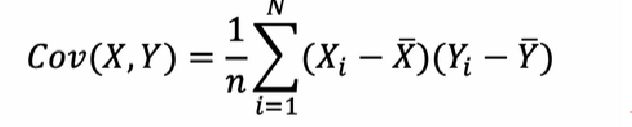
correlatie

gestandardiseerde maat voor de lineaire afhankelijkheid tussen twee kansvariabelen

door standardisatie is de meeteenheid interpreteerbaar

vaak symbool rho p

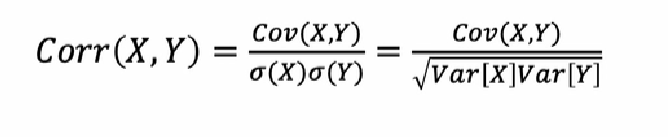
correlatie =! causaliteit

de aanwezigheid van correlatie tussen twee kansvariabelen X en Y duidt niet noodzakelijk op de aanwezigheid van een relatie tussen die kansvariabelen

wanneer zijn correlaties “spurious”

wanneer zij duiden op een lineaire afhankelijkheid tussen de variabelen, terwijl ze in feite onafhankelijk zijjn van elkaar