APPC Mnemonics

Horizontal Asymptote Limit Notation

lim x- +infinity f(x) = #

As input value increases without bound, the output values approach #

FLOOR

a f(b(x-h) + k

VERTICAL CHANGES

stretch = a>1
compress = a<1

a f(b(x-h) + k

HORIZONTAL CHANGES

stretch = b<1
compress = b>1

arctan(x)

Domain = [-infinity, +infinity]
Range = [-pi/2 , pi/2]

Quadrants 1 & 4

which of the following gives the graph of the displacement of 𝑃 from the 𝑥-axis as a function of 𝜃 ?

𝑦=cos𝜃. This response is the horizontal displacement of 𝑃 from the 𝑦-axis instead of the vertical displacement of 𝑃 from the 𝑥-axis.

𝑦=sin𝜃. The vertical displacement of 𝑃 from the 𝑥-axis

find x's (FRQ)

f(x)=# when x=# and x=#

why not invertible?

there are outputs of f that are not mapped to unique input values

"To define a function, for every x there must only be 1 y."

"FAILS HORIZONTAL LINE TEST IS NOT ENOUGH"

New features!

P.S

Zoom fit
Trace

On Unit circle, big middle ones are +30 and the others are +15

​​𝑔 is best modeled by a quadratic function, because

the change in the average rates of change over consecutive equal-length input-value intervals is constant.

On a semi-log plot

if you have exponential values, the dots appear linear.

To find the sum of nth terms on a sequence

Use Sn = n/2 (a1+an)

S(#: number it asks for) = #/2 (1st term + an from arithmetic sequence)

an = a1 + d(n-1)
d = +- to get to next term

Linear ROC

ROC is constant at any interval

Quad ROC

2nd differences of output values are constant

Polynomial ROC

nth differences of output

Values are constant of equal length input intervals

Exponential ROC

output values are proportional over ELII

EXES DONT X!!!

x+

y*

Logarithmic ROC

Proportional input values result in constant change in output values

x*
y+

[a,b]

ROC = (f(b) - f(a))/b-a

Vertical asymptote limit notation

lim x- # from - (Left) f(x) = +- infinity

As input value approaches # from the left, the output values decrease without bound.

WALL

tiny # is floor, +- infinity is clock on WALL

n < d

limit notation =

y = 0

D is big? You get 0 play!

n = d

ratio of leading coefficients

n > d

If d is 1 bigger, SLANT

Limit notation = +- infinity to +- infinity

Arithmetic sequence

an = ak + d(n-k)

an= a0 + dn

Geometric sequence

gn = gk(r)^(n-k)

gn = g0r^n

arccosx

Domain = [-1,1]
Range = [0, pi]

Quadrants 1 & 2

arcsinx

Domain = [-1,1]
Range = [-pi/2 , pi/2]

Quadrants 1 & 4

Pythagorean Identities

sin²∅ + cos²∅ = 1
tan²∅ + 1 = sec²∅
cot²∅ + 1 = csc²∅

sin²∅ + cos²∅ =

1

tan²∅ + 1 =

sec²∅

cot²∅ + 1 = cosec²∅

csc²∅

Reciprocal Identities

sinθ = 1/cscθ ; cscθ = 1/sinθ
cosθ = 1/secθ ; secθ = 1/cosθ
tanθ = 1/cotθ ; cotθ = 1/tanθ

csc∅

1/sin∅

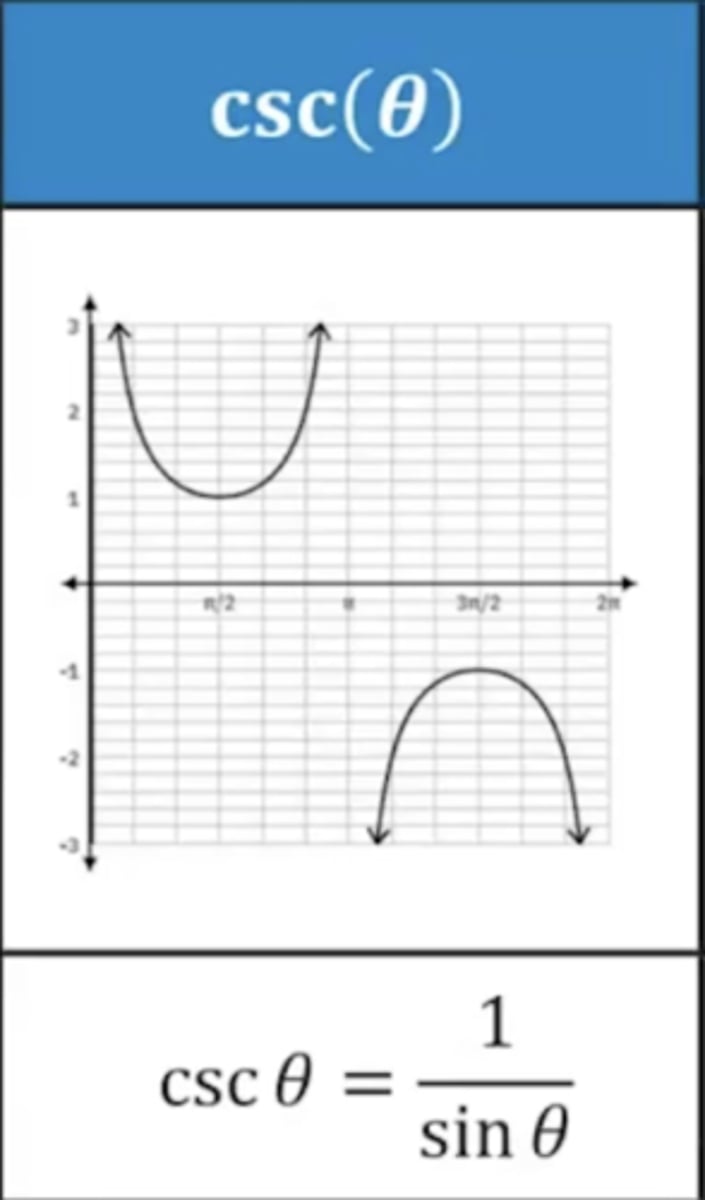
sec∅

1/csc∅

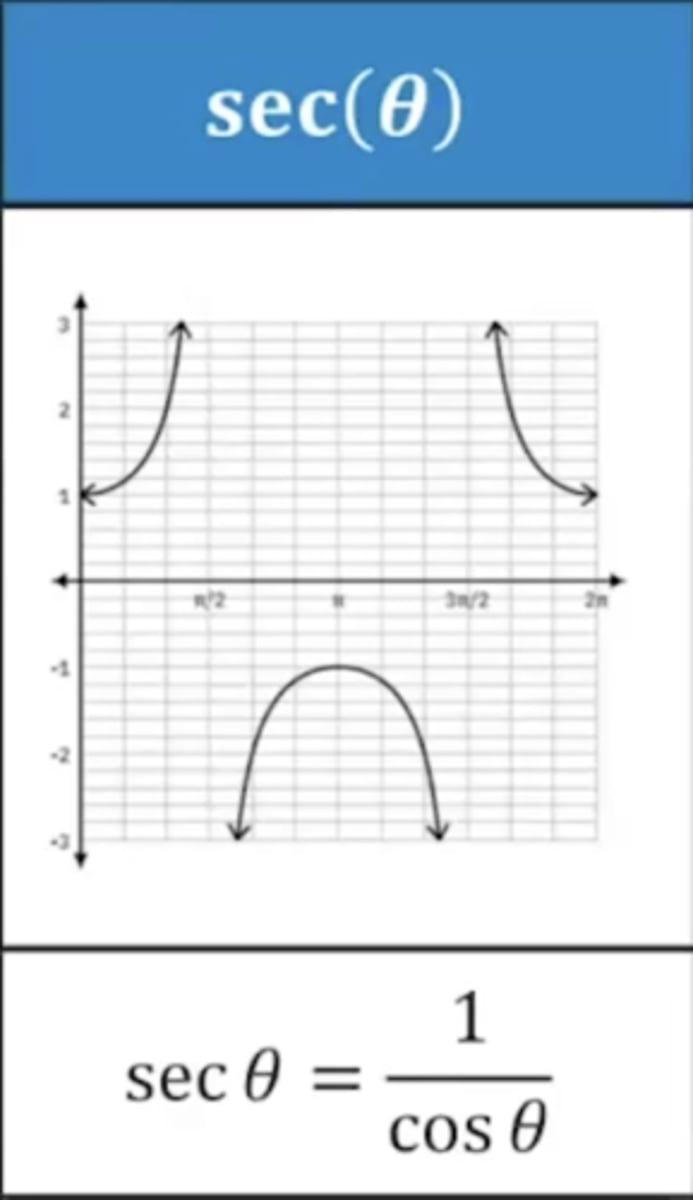
cot∅

1/tan∅
cos∅/sin∅

Always decreasing!

sin∅

1/csc∅

cos∅

1/sec∅

tan∅

1/cot∅

sin∅/cos∅

sin (2∅)

2sin∅cos∅

cos(2∅)

cos^2∅-sin^2∅
2cos^2∅ - 1
1 - 2sin^2∅

sin(u+u)

sin2u = sin u cos u + sin u cos u

cos (a+-B)

sin (a+-B)

cos a cos B +- sin a sin B

cos thinks the signs are opposite !

sin a cos B +- cos a sin B

sin thinks they have the same sign and sit upfront together with siblings in the back!

rectangular to polar

complicated

r^2 = x^2 + y^2

arctan

polar to rectangular coordinates

x = r cos(∅)
y = r sin(∅)

polar to complex

a + bi = r (cos∅ + i sin ∅)

r is only ever

+

Frequency

Reciprocal of Period

Rotation / Time

R comes first in the word 'Frequency'.

cos ∅

sin (∅ + pi/2)

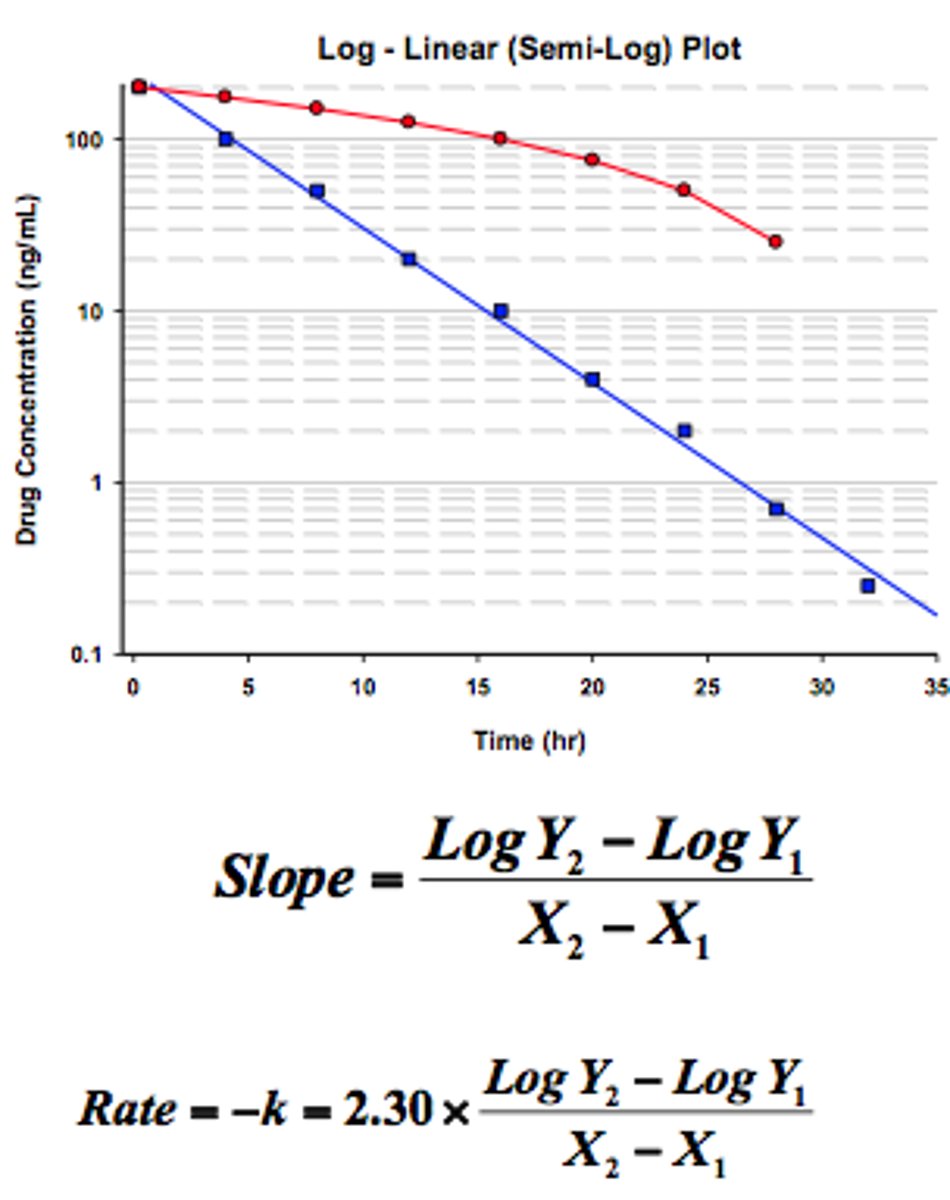
Semi-log plots

convert exponential curves into straight lines

• Something that curves up becomes a straight line with positive slope
• Something that curves down becomes a straight line with negative slope
• For exponential decay, a semi-log plot graphs log of amount vs time
• For exponential decay, a semi-log plot is a straight line with negative slope
• Semi-log plot intercepts the x axis where the original y value is 1

Odd

f(-x) = -f(x)

negative son - negative parent :(

Even

f(-x) = f(x)

negative son becomes positive son :D

2pi/b

b =

Period

2pi (or pi)/period

To find VA of tan functions

set inside = to pi/2

cos graph

Domain = (-infinity, +infinity)
Range = [-1,1]
Period = 2pi

starts at max 1
hits pi/2
bottoms out at (pi,-1)

sinx graph

Domain = (-infinity, +infinity)
Range = [-1,1]
Period = 2pi

starts at 0
hits (pi/2,1)
hits pi
bottoms out at (3pi/2,-1)

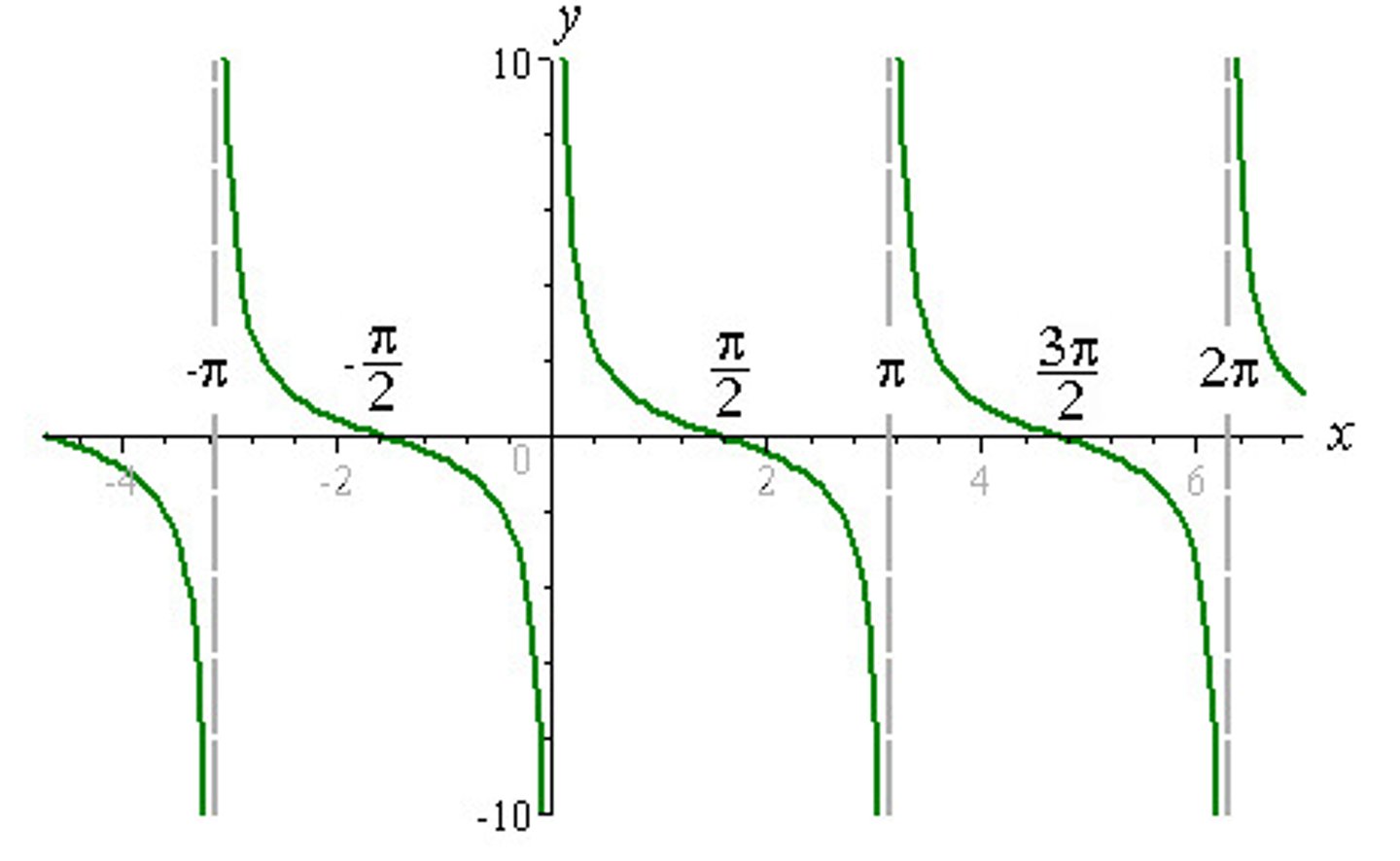
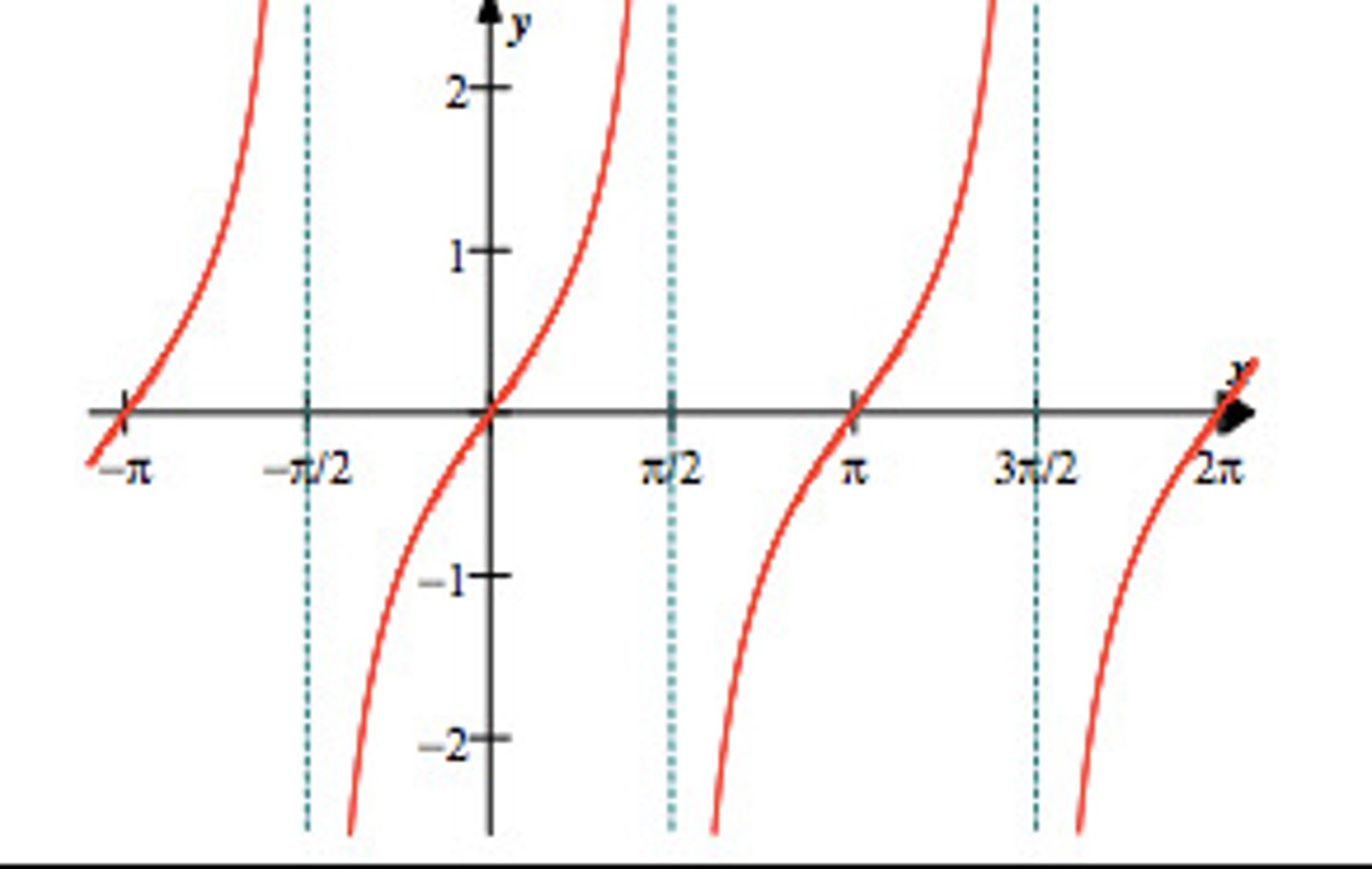
tanx graph

Range = [-infinity,+infinity]
Period = pi

always increasing
pi/4 where it goes straighter

Polar calculator

mode - PoL (∅) - Radian

Symmetry across y-axis

Symmetry across y-axis

sin∅

cos∅

# - # cos∅

Dented circle with inner loop

3sin(2∅)

Rose petal because no +-

Odd #

Same amount of petals

Even #

Twice amount of petals

Pascal's Triangle

(x+2)^5

2 is y-value

x DECREASES

y starts at 0 but INCREASES

pascal has decreasing x's because he is moving on!

Exponential Function

ab^x

a - Initial Value

b - Must be +, but not 1

Growth - a > 0 b > 1

Decay - a > 0. 0 < b < 1

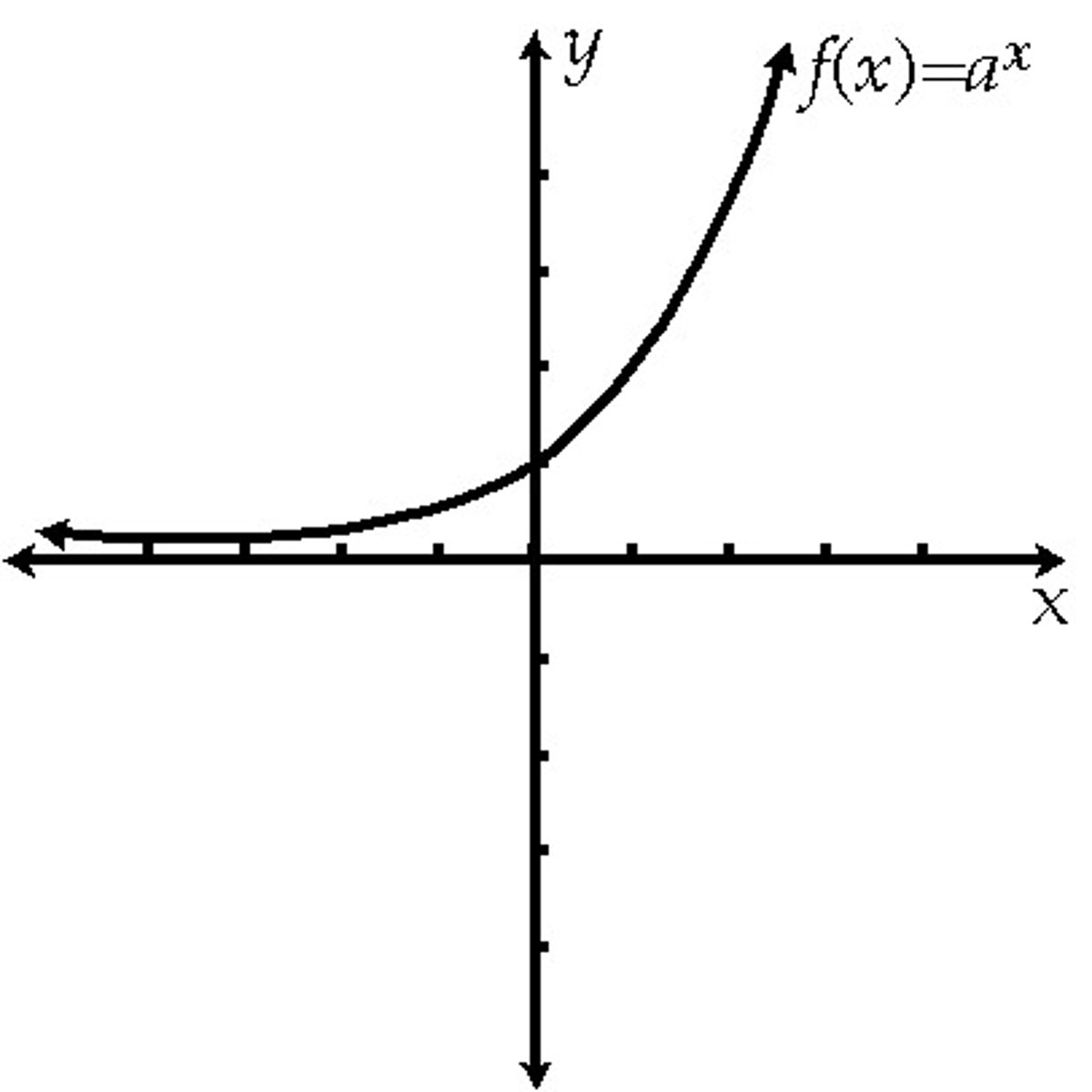
Exponential Growth

a > 0 b > 1

3(1.5)^x

1/120 (2)^x

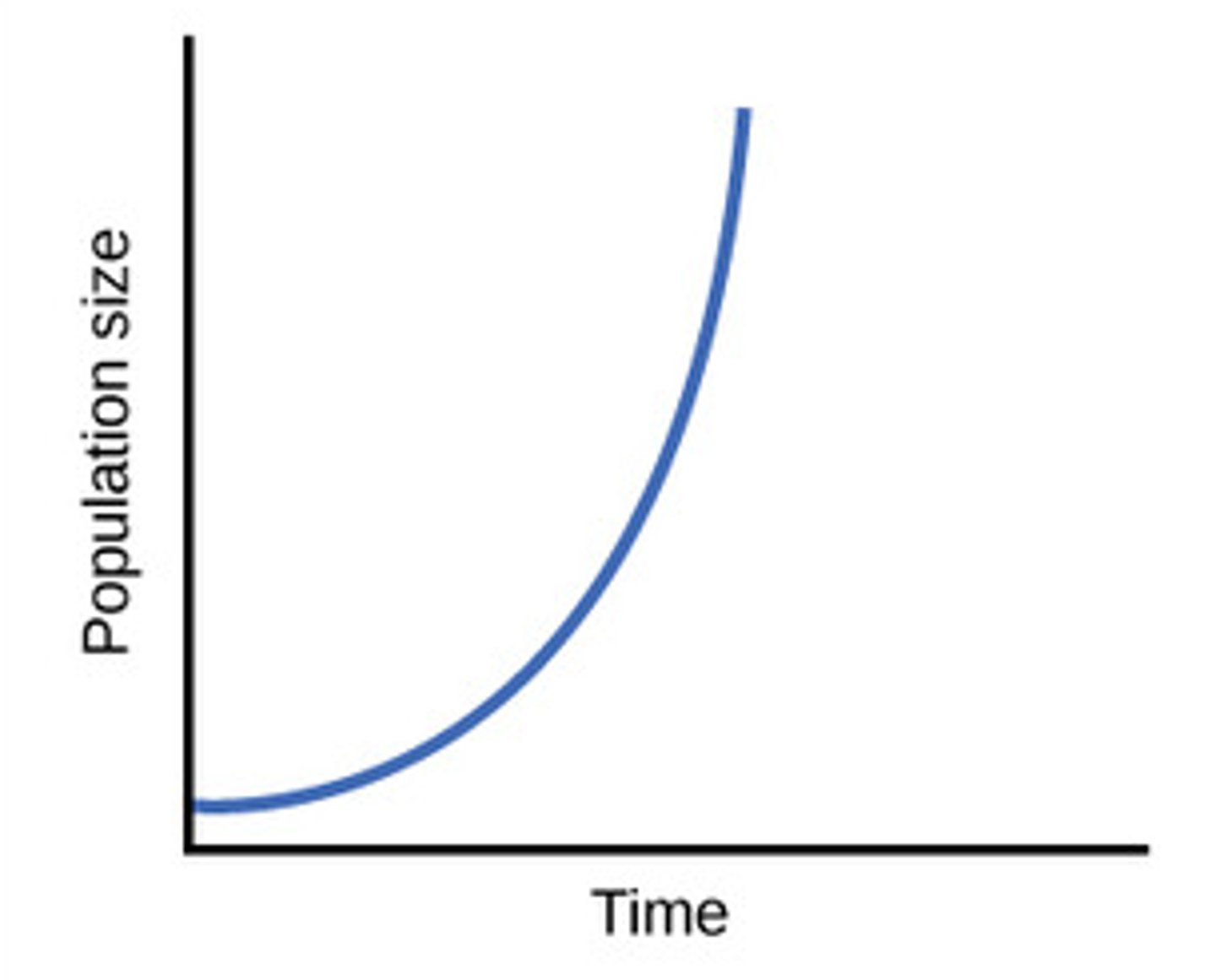
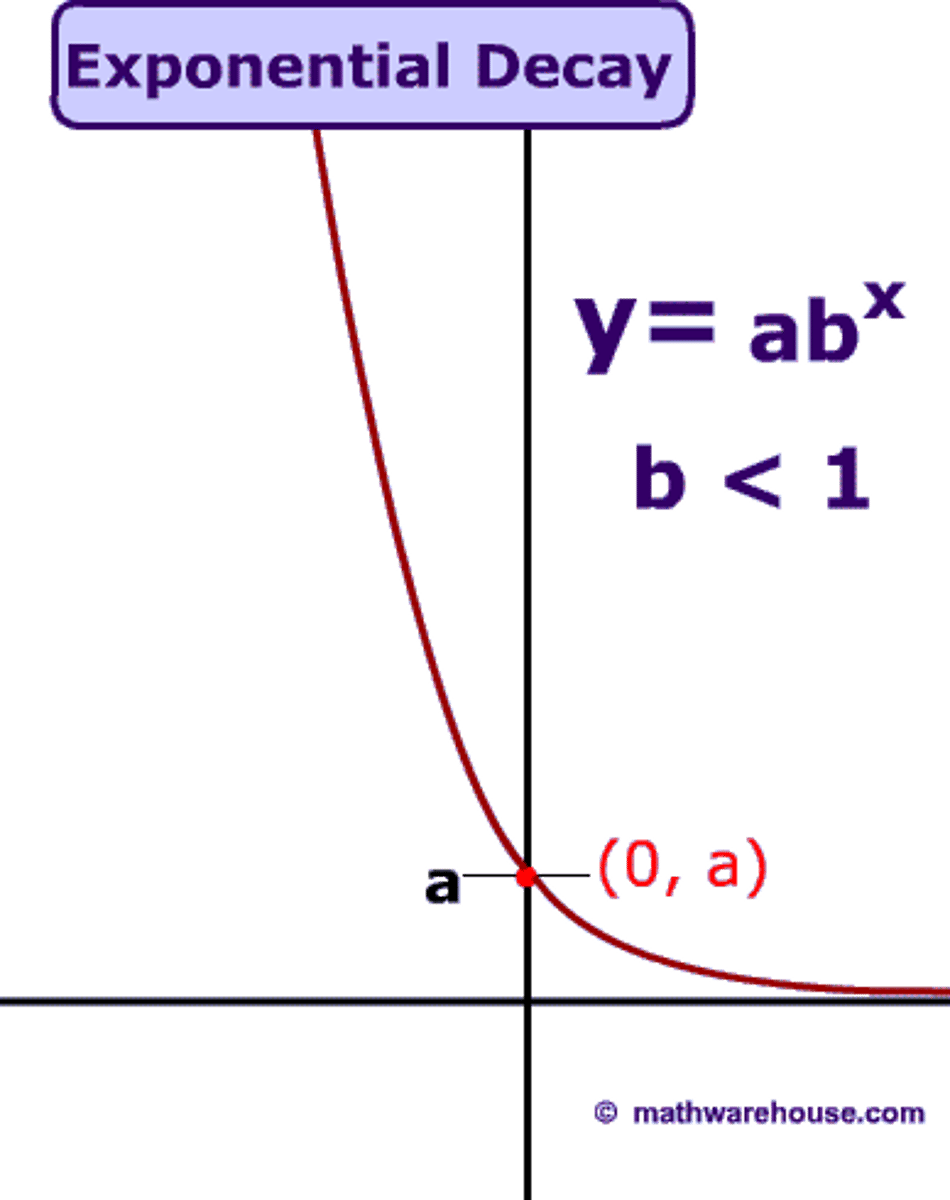
Exponential Decay

a > 0 0 < b < 1

5/2 (0.012)^x

0.013 (2/5)^x

a value in exponential will always be

+

To find b in exponential graph...

have two sets of values

6 = ab^0 (Initial Value)'
a = 6

3 = ab^1 (1,3) was a value
b = 1/2

In order for a function to be invertible...

If each output value is mapped by a unique input value.

Passes vertical line test

We may need to restrict domains for this...
(ex: Logs/Exponents)

Extraneous Solutions in Logs

plug it back in and get a negative log?

PLUG IT INTO O.G QUESTION

Nope.

Residual

actual value - predicted value

tanx

sinx/cosx
VA: pi/2 3pi/2

point slope form (Needed for FRQ asking use ROC to estimate x=#)

y-y₁=m(x-x₁)

In order to see if a function can be inversible,

it must pass the horizontal line test

in circle problems where it asks to make a sin/cos function,

AMP = RADIOUS

ferris wheel radius is 30, amp is 30.

when it crosses through x-axis

ODD multiplicity (doesn't bounce)