Ideal Gas Heat Capacity

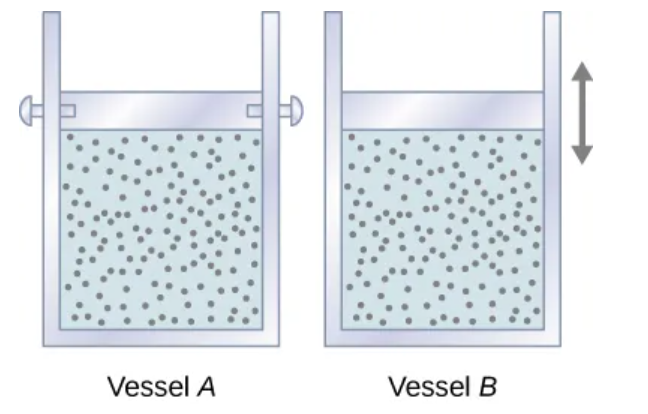
Two vessels are identical except that the piston at the top A is fixed, whereas that at top of B is free to move against a constant external pressure p.

Cv

• Molar Heat capacity measured while volume remains constant

• Meaning gas does not work

• All the added heat increases internal energy

Cp

• Molar Heat capacity measured at constant pressure

• The gas expands and does work

• So extra heat is required compared to Cv

Isochoric Process

A thermodynamic process where volume stays fixed, so no work (W = 0) is done. Heat is added directly increases internal energy.

Isobaric Process

• A process where pressure stays constant.

• Added heat goes partly into work pdV

• And partly into raising internal energy,

dW = pdV = nRdT

Mathematical Representation of the work at a constant pressure (when a gas expands)

dQ = n(C_V)dT

Mathematical representation of the heat at a constant volume. (Because dW = 0, all heat increases internal energy)

dQ = n(C_p)dT

Mathematical representation of the heat at a constant pressure.

temperature

Internal energy of an ideal gas depends only on the ___________

dEint = n(C_V)dT

Mathematical representation of the Internal energy inside an ideal gas for any temperature change.

Mayer’s Relation

Derived from applying the first law to Isochoric and isobaric heating of an ideal gas.

Cp = Cv + R

Mayer’s Relation

Because at constant pressure, the gas must do expansion work, so it needs extra heat compared to constant volume.

Why Cp is greater?

Degrees of Freedom

Independent ways a molecule can store energy

C_V = (d/2)R

Formula that provides the relationship between the Degrees of Freedom and Heat Capacity

Cv = (3/2)R

Cv formula applicable for monoatomic gases like Helium, Neon, and Argon gas

Cp = (5/2)R

Cp formula applicable for monoatomic gases like Helium, Neon, and Argon gas

Cv = (5/2)R

Cv formula applicable for diatomic gases Oxygen and Nitrogen gases at room temperature.

Cp = (7/2)R

Cp formula applicable for diatomic gases Oxygen and Nitrogen gases at room temperature.

Cv = 3R

Cv formula for polyatomic gas as vibrational modes add extra energy storage.

Cp = 4R

Cp formula for polyatomic gas as vibrational modes add extra energy storage.

Cp - Cv = R

Universal Difference of Heat Capacities for all dilute gases regardless of molecular type.

Because vibrational mode contribute even at room temperature.

Why does real gases have slightly higher heat capacities?

Vessel A Behavior

No volume change → no work → all added heat raises internal energy

dEint = dQ

Vessel B Behavior

Gas expands → Work done → Heat splits into:

• Raising internal energy

• Doing pdV work

• dQ = dEint + pdV

pdV = nRdT

pdV for constant pressure gas

(Cv)ndT = (Cpn - Rn)dT

Internal energy path independence which is a must match for both isobaric and Isochoric paths because internal energy is a state function.