Discrete Math Final Exam Review

Recursion

when an object's definition relies on that object

e.g. 2^n = 2x2^(n-1)

Induction

the proof technique used to demonstrate facts about recursive definitions

Set

(loosely speaking) is a collection of objects called elements

e.g. if this class is a set, you are an element

We write x ∈ X when x is an element of the set X

list or rooter notation

the set of whole numbers between 1 and 10 inclusive

{1,2,3,4,5,6,7,8,9,10}

list or rooter notation

is the set of positive whole numbers

{1,2,3,4,...}

Set builder notation

elements are described by some rule or property

set builder notation

the set of whole numbers between 1 and 10 inclusive

{x | x is a whole number and 1≤x≤10}

set builder notation

the set of positive whole numbers

{n | n is a positive whole number}

N

natural numbers

{0,1,2,3,4,...} 0 only counts in CSCI

Z

integers

{...,-2,-1,0,1,2,...}

Q

rational numbers

{(p/q) I p, q ∈ Z and q ≠ 0}

where p and q are both integers

R

real numbers

rational numbers and everything in between

e.g. π,3,(1/3)

subset

given two sets X and Y, we say Y is a subset of X if every element of Y is also in X.

Y⊆X

empty set

set that has no elements

{} or Ø

a subset of every set

collection

set of sets

Power set

collection of all subsets of X

P(X)

e.g. X={1,2,3}

P(X)= {Ø, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}}

Union

the set of all elements in X or in Y

X={1,3,5}

Y={2,4,6}

X∪Y={1,2,3,4,5,6}

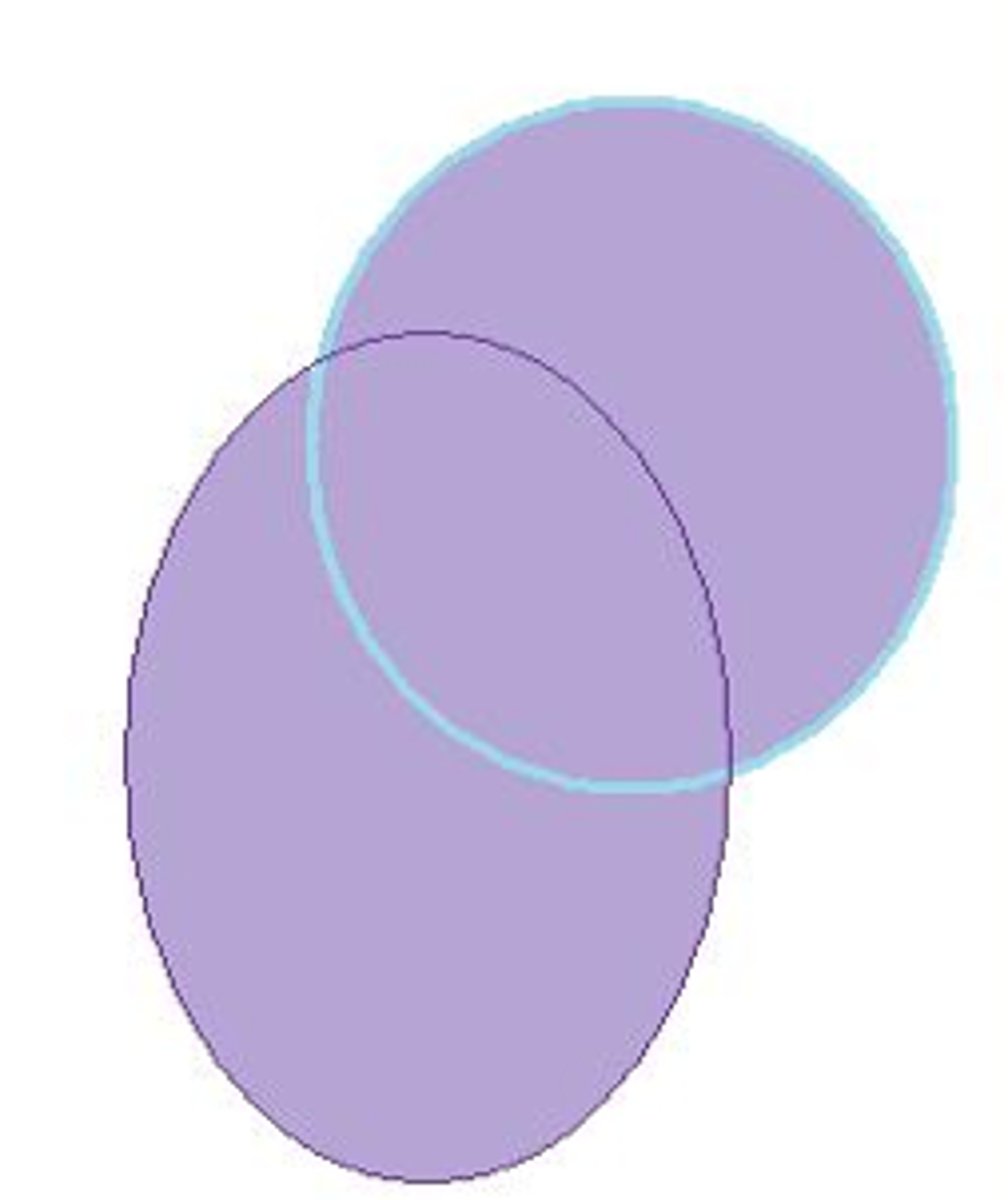
intersection

the set of all elements in X and Y

X={1,2,3}

Y={3,4,5}

X∩Y={3}

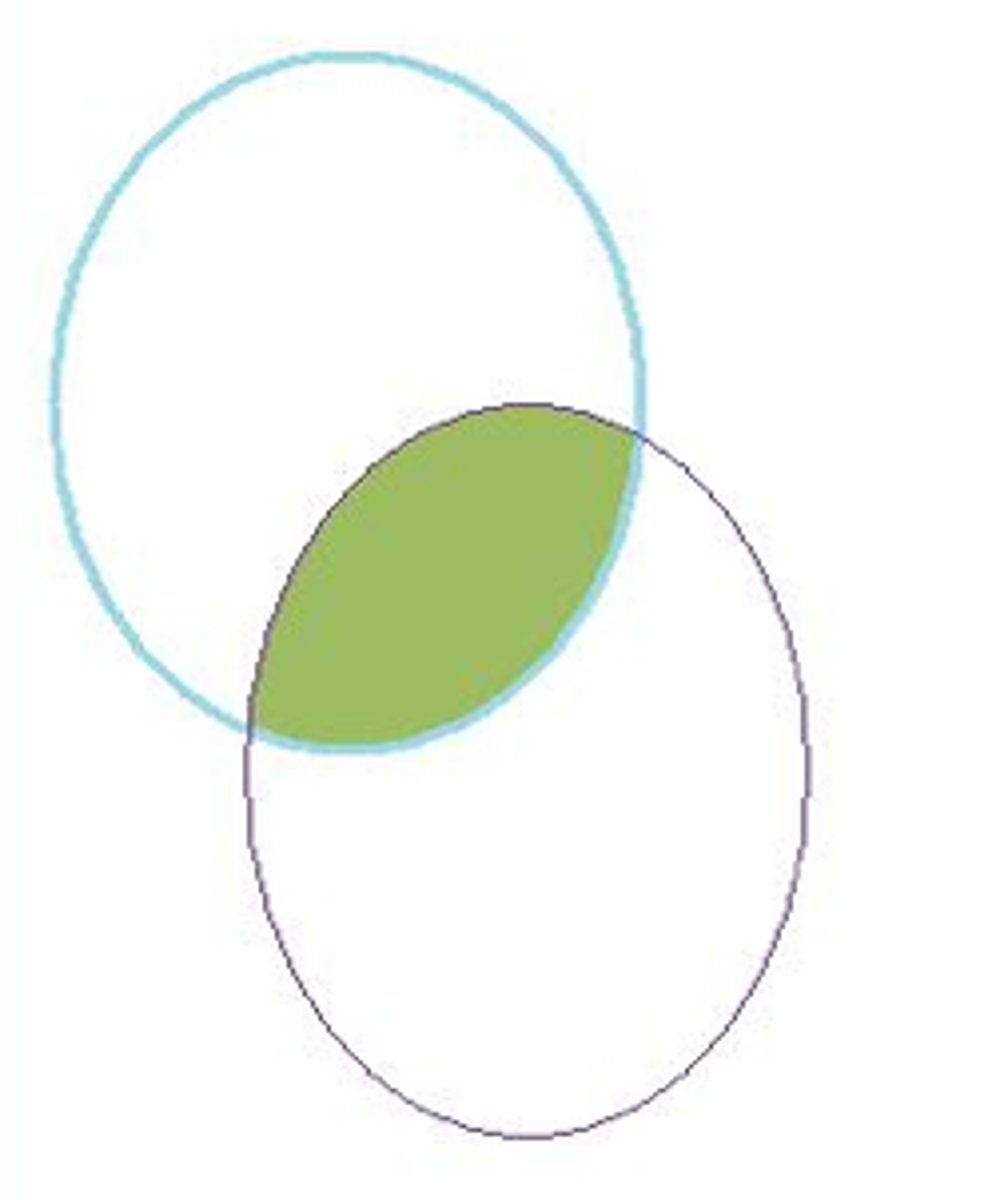
Relative Complement

the set of all elements in X but not in Y

X-Y

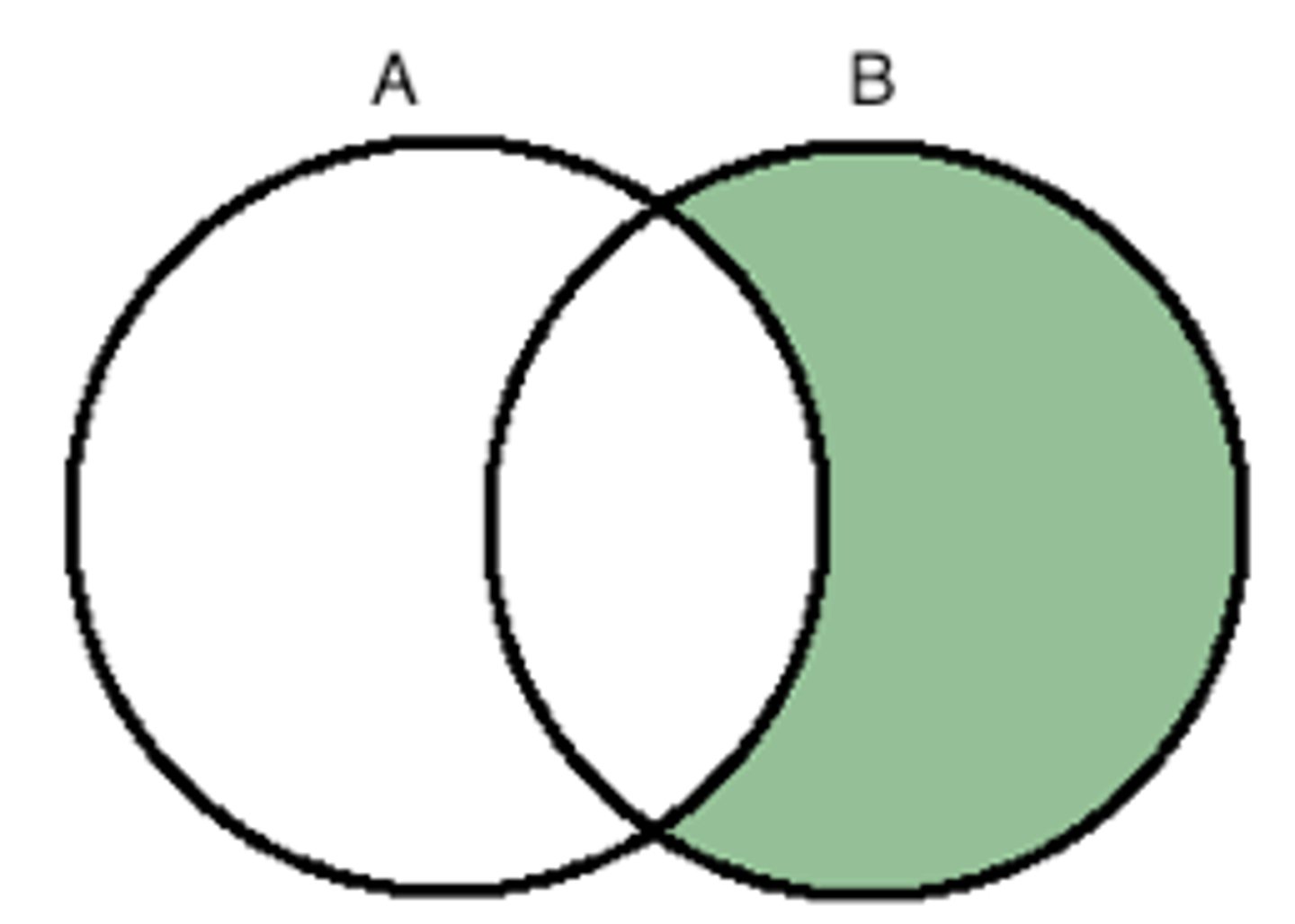
universal set

the set containing all objects or elements and of which all other sets are subsets.

e.g. all math majors must take math 160

universal set: CCU

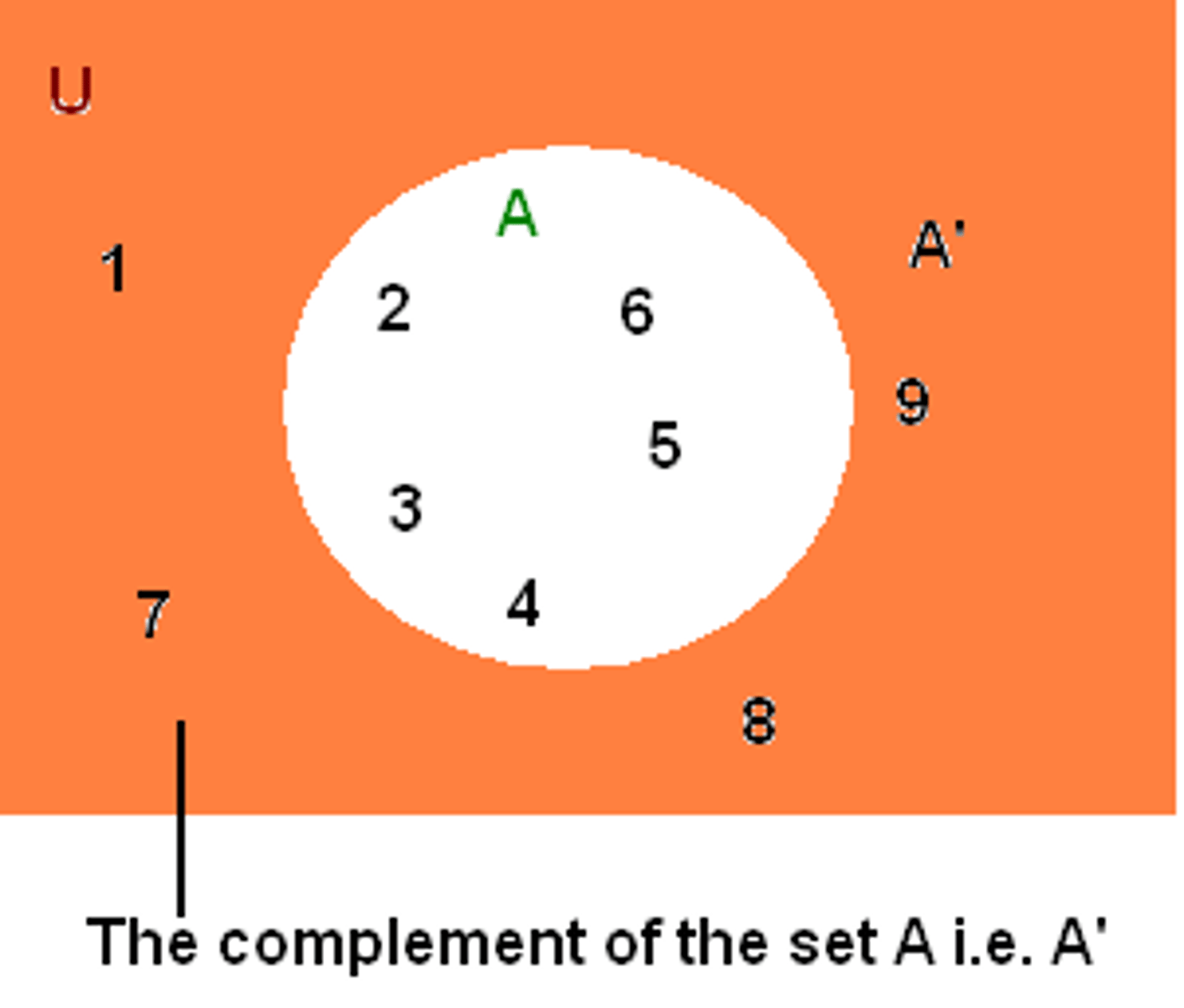
complement

is the set of all elements ( in the universal set but) not in X

X ( with a line over the top)

Cartesian Product

the set of all ordered pairs of elements whose first coordinate is in X and whose second coordinate is in Y

X×Y

{(x, y) | x ∈ X and ∈ Y}

two sets are equal if...

they have exactly the same elements

cardinality

the number of elements (if finite) in X

|X|

e.g. X={1,2,a}

|X|= 3

|A+B|= the number of elements in both set A and set B

union rule

|X∪Y|= |X| + |Y| - |X∩Y|

statement

a sentence that is true or false

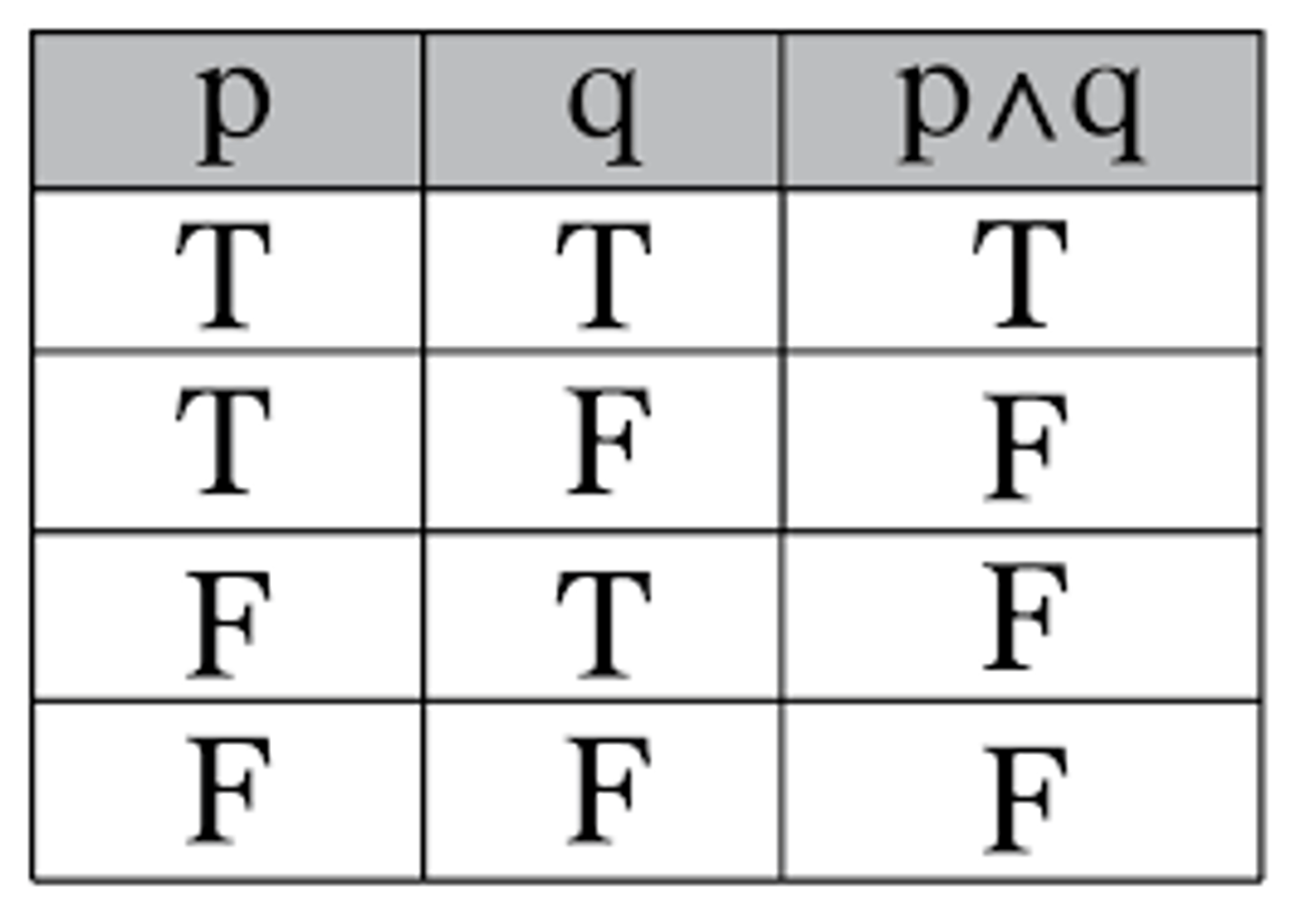
conjunction

if p and q are statements, their conjunction in p⋀q (p and q)

the conjunction is true when both p and q are both true and false otherwise

truthtable

a device that lets us tell whether a compound statement is true given whether its pieces are true

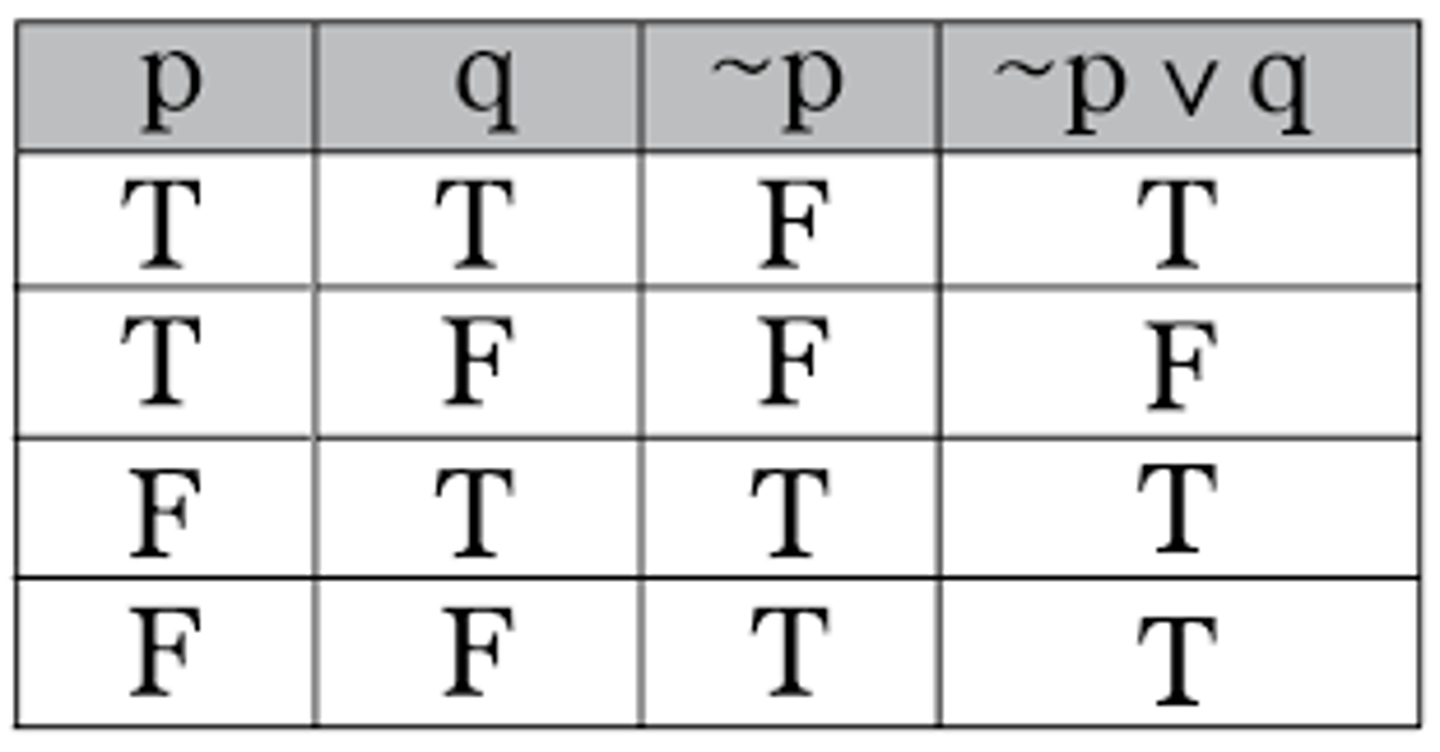
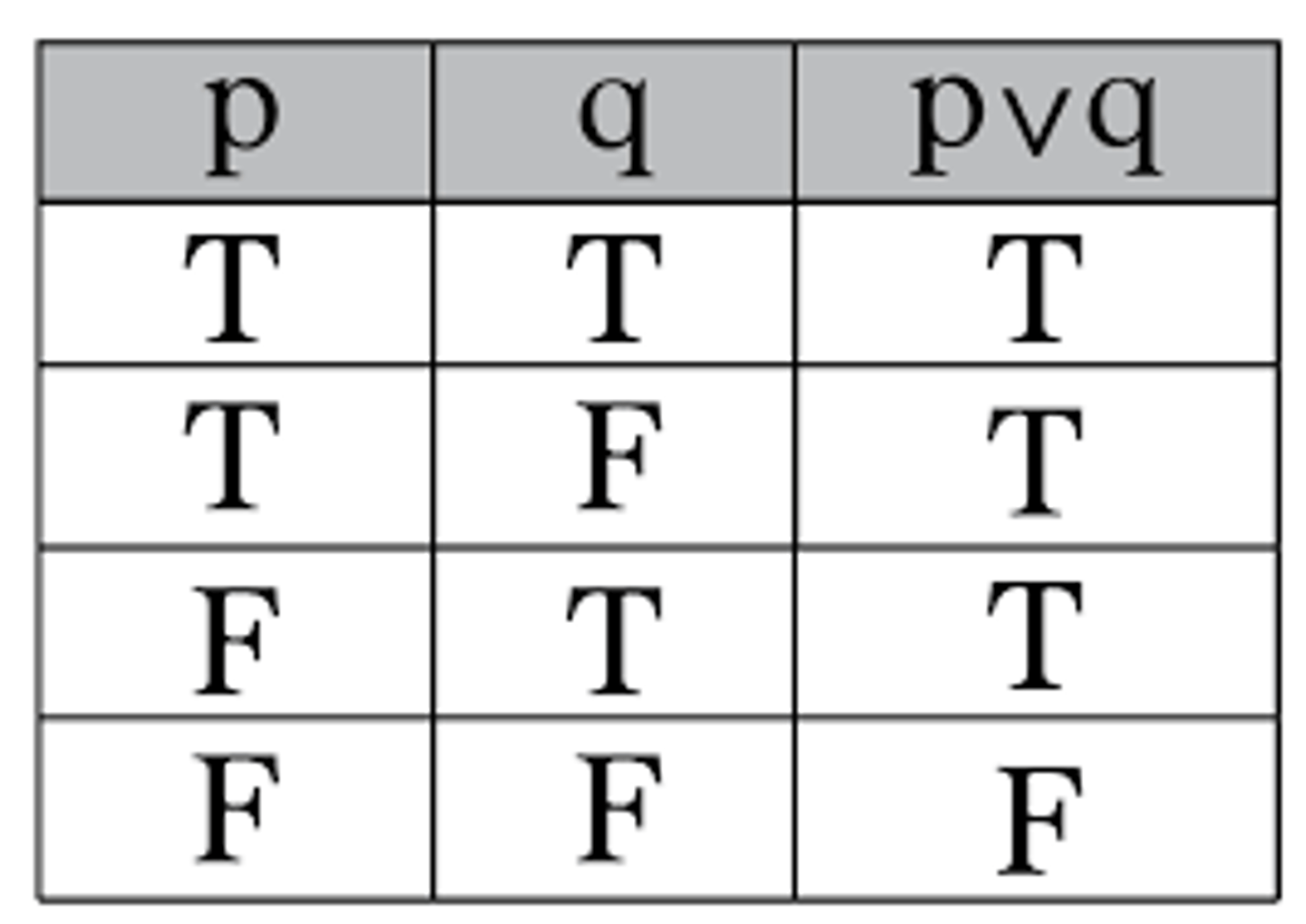
disjunction

p∨q (p or q)

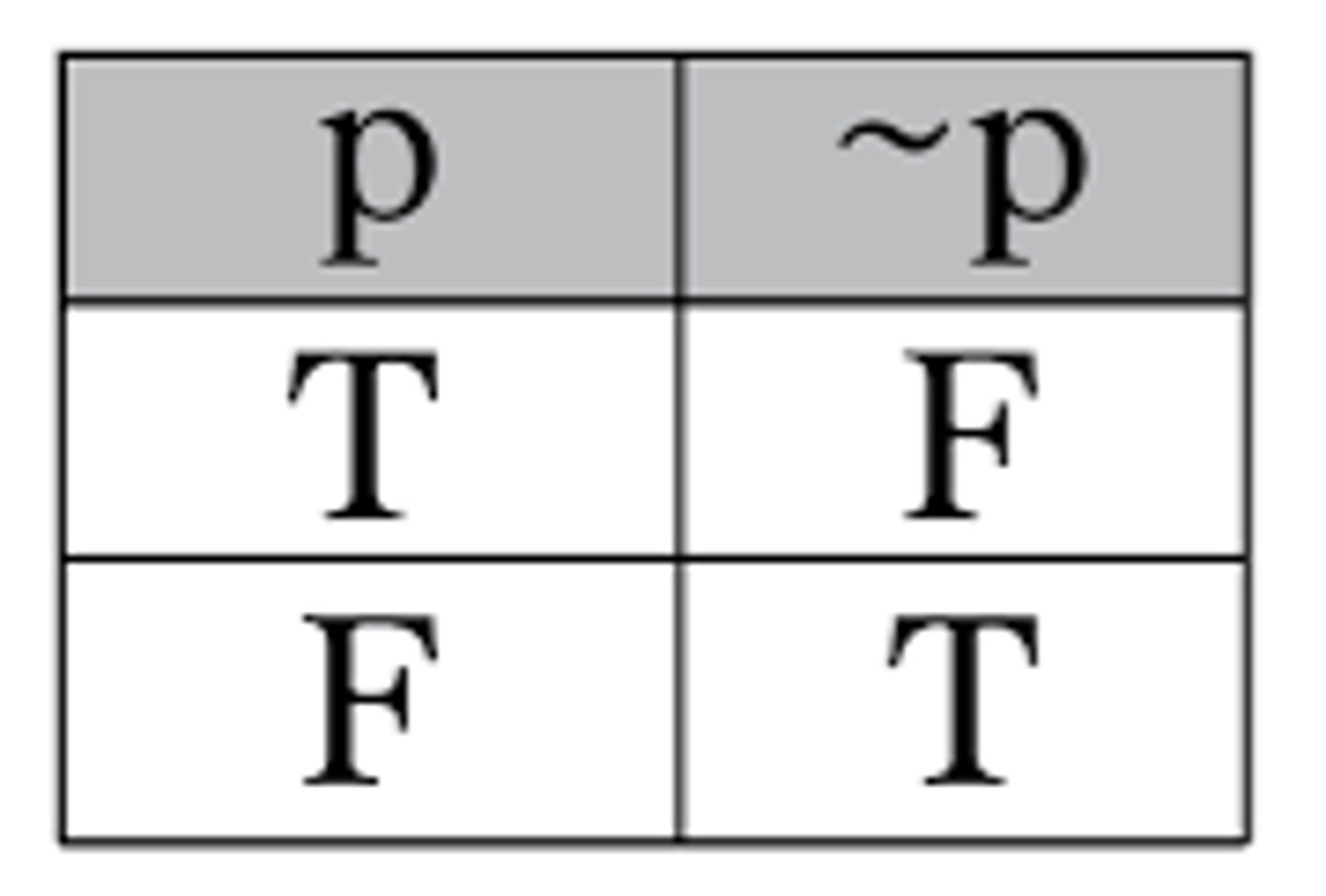
Negation

¬p or ~p (not p)

Exclusive-OR

p⊕q (either p or q); p or q, but not both

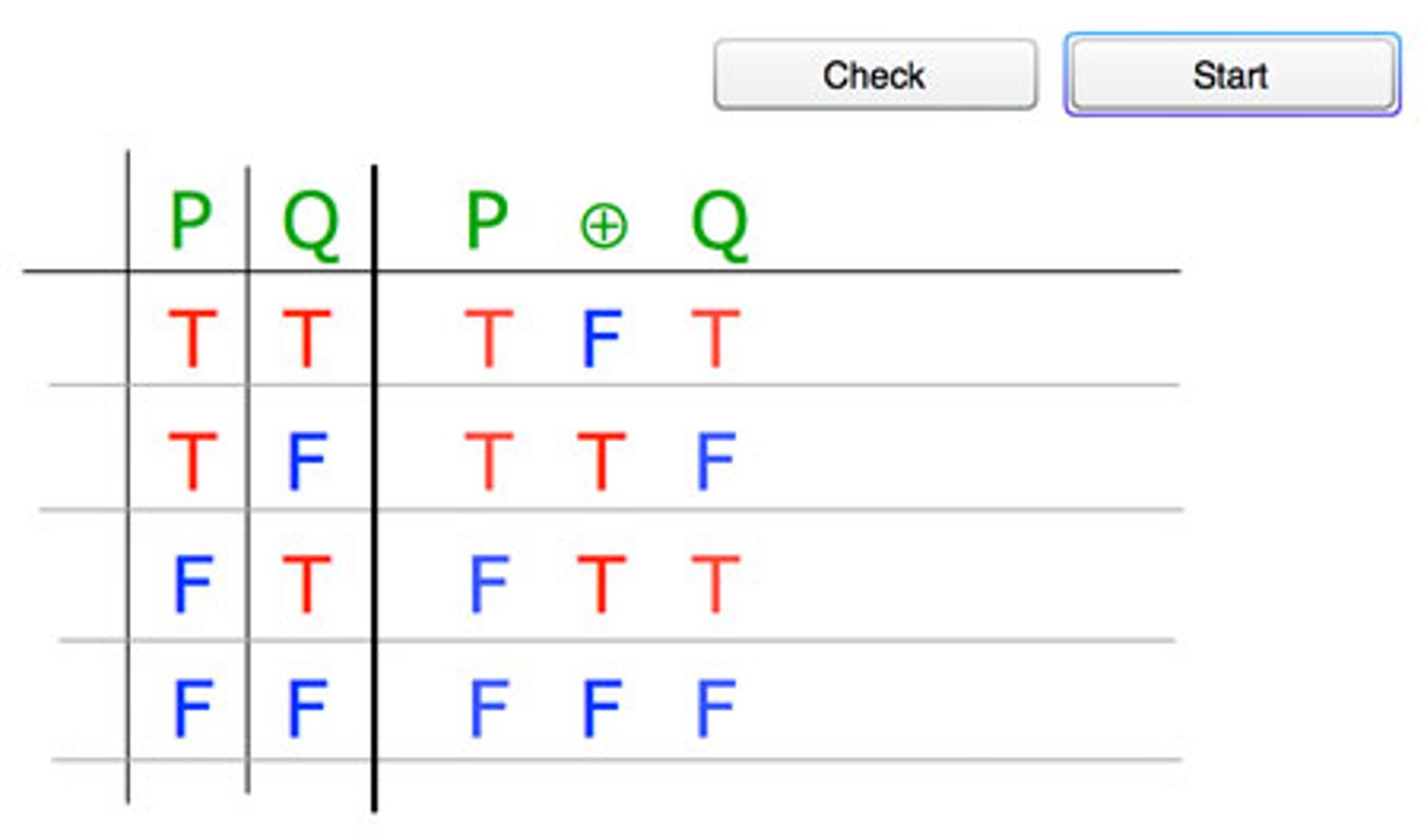
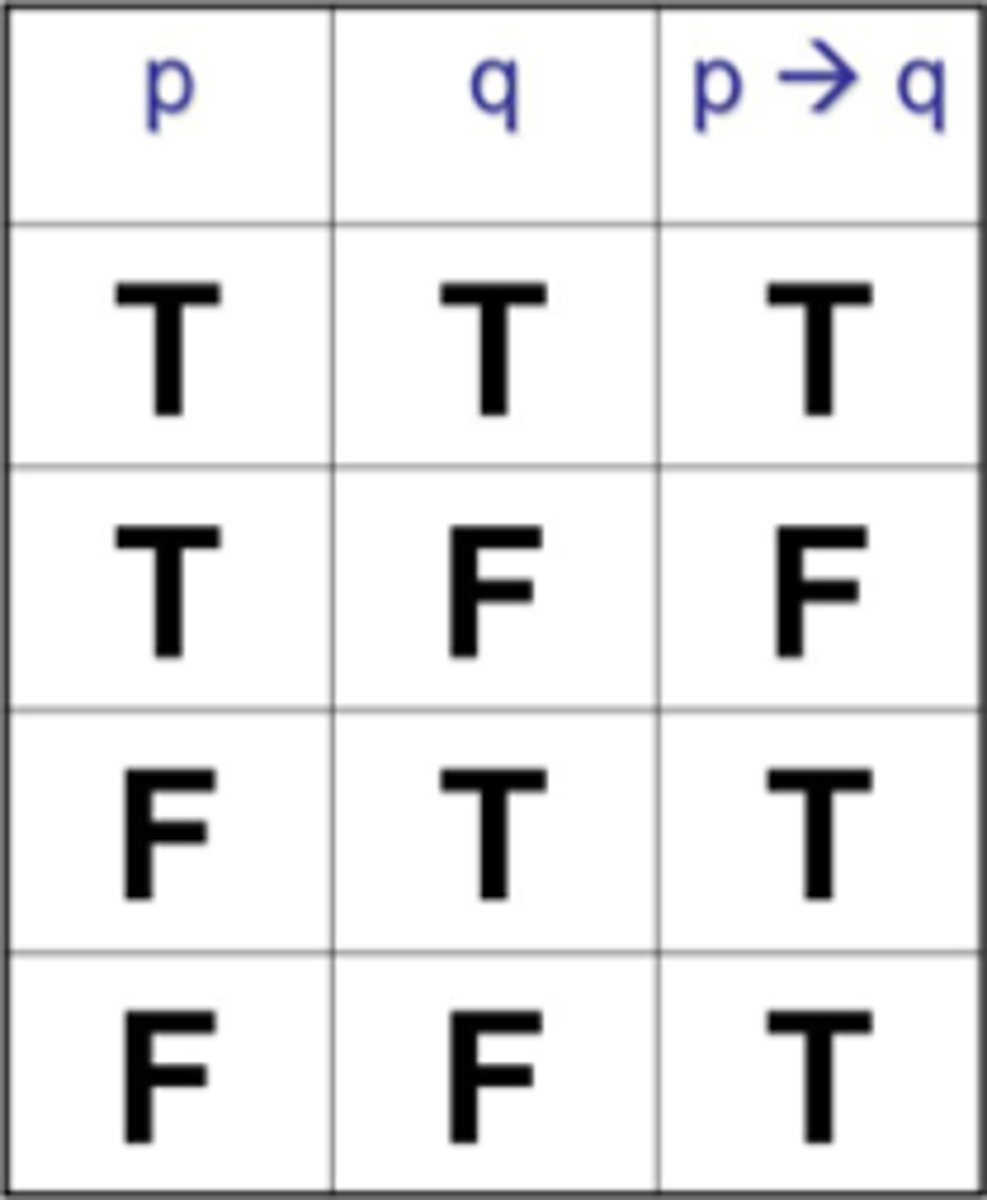
conditional

p→q

"if p then q",

"p implies q",

"p is sufficient for q"

p does not have to be true

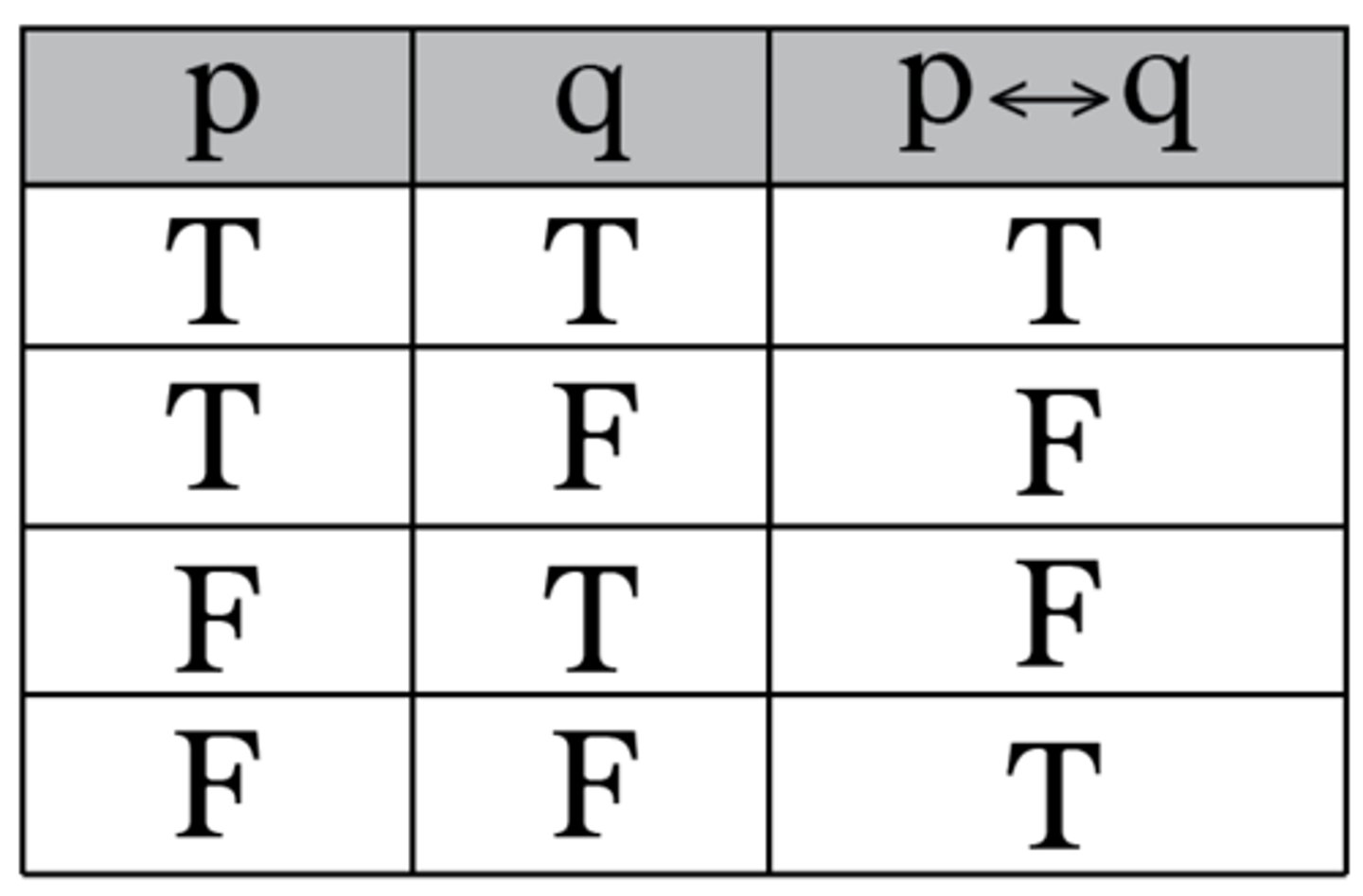
biconditional

p↔q

"p if and only if q"

"p is necessary and sufficient for q"

"p and q are equivalent"

antecedent of p→q

p

consequent of p→q

q

converse of p→q

q→p

inverse of p→q

~p→~q

contrapositive of p→q

~q→~p

two statements φ (phi) and ψ (psi) are equivalent if...

they have the same truth table (value), or if φ↔ψ is always true and we write φ≡ψ

a statement φ is a tautology if...

it is always true, or φ≡T

a statement φ is a contradiction if...

it is always false, or φ≡F

knights and knaves

knights speak the truth

knaves speak falsely

the right answer from truth table is where they match

order of operations

P

E

M

D

A

S

order of operations: logic

not ¬

and/or ∧/∨

conditional →

biconditional ↔

de morgans law logic and sets

¬(p∧q)≡ ¬p∨¬q ( and vice versa)

(complement of X∩Y)= (complement of X) ∪ (complement of Y) - and vice versa

transitivity

φ≡ψ (phi = psi)

ψ≡γ (psi = gamma)

then φ≡γ (phi = gamma)

predicate

a function whose domain is some universe of objects being discussed and whose output is T or F

Q(x)

universal quantifier

declares that a statement is true for every element of the domain

symbol ∀

∀x "for all x"

existential qunatifier

declares that a statement is true for (at least) one member of the domain

∃

∃x "there exists an x"

predicates

∀xP(x) "every x is a P"

∃xP(x) "some x are P"

binary

an example of a recursive number

(100101011100)2 -base 2

= 1x2^11 + 0x2^10 + 0x2^9 + 1x2^8 + ...

=2048 + 256 + 64 + 16 + 8 + 4

=2396

sequence

a list of objects

{Xn} nth term is Xn

closed form of a sequence

an explicit expression

recurrence relation

the terms are defined with respect to previous terms

Summation

If {Xn} is a sequence this is the sum of its terms

Xk, Xk+1, Xk+2,...Xn

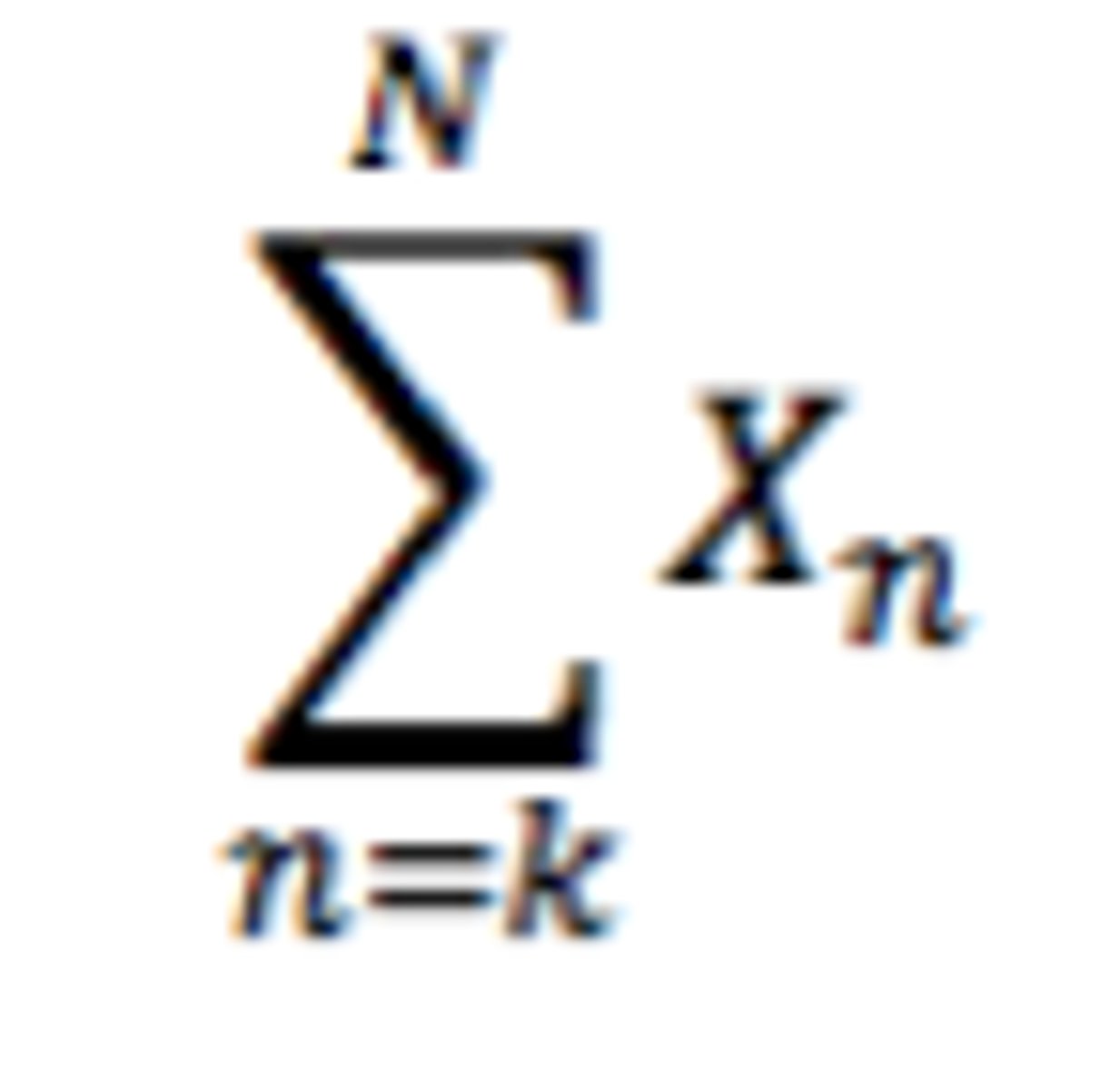
Recursive summation

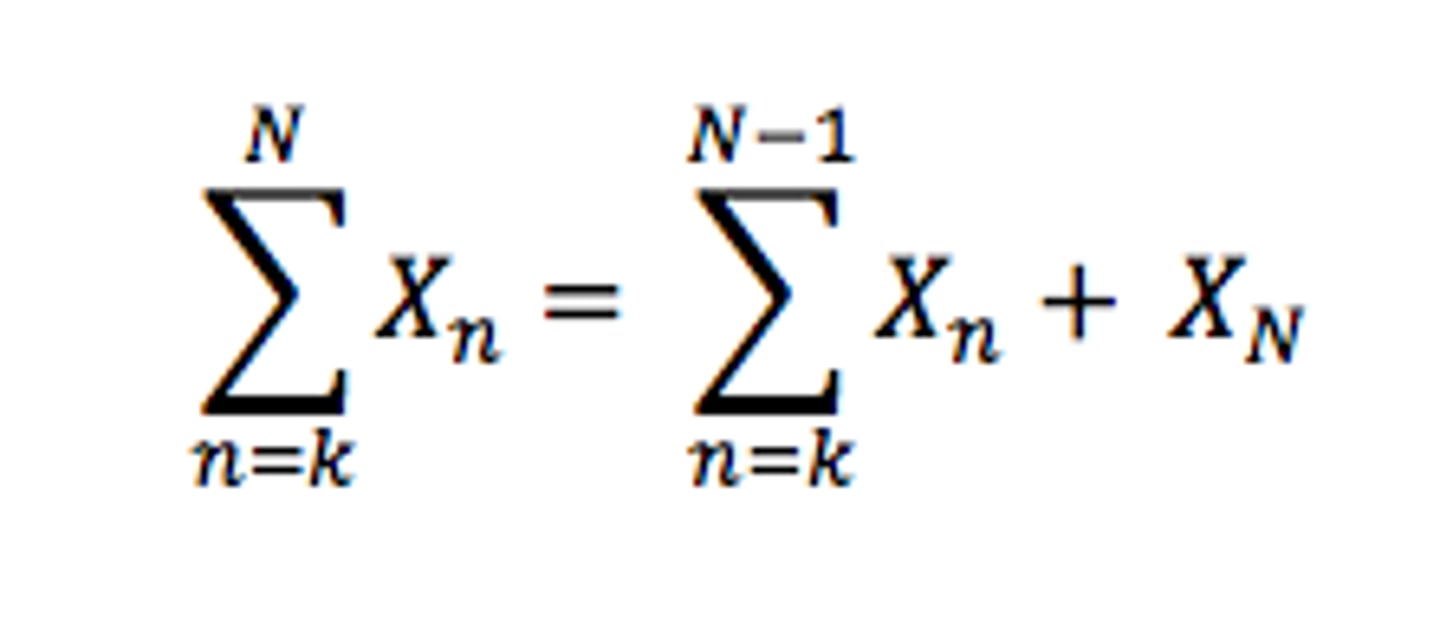
Linearity summation

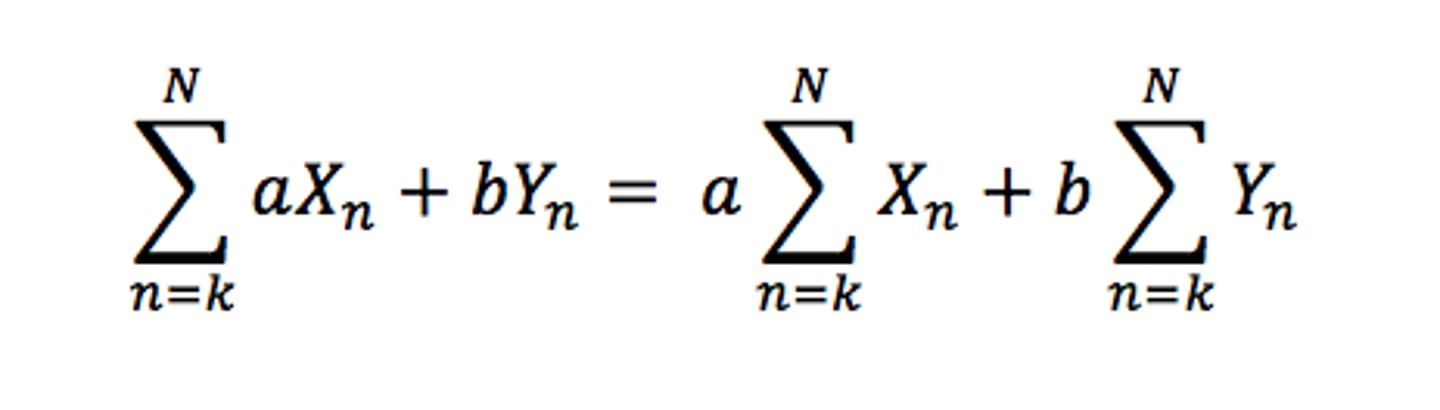
proofs

we prove statements of the form p→q by assuming p is true and making a sequence of valid equivalences or rules of inference to conclude q is true.

proof by contradiction

of p→q, assumes that ~(p→q) ≡ p∧~q and derive a contradiction

by proving the opposite as nonsense, you get what you originally set out to prove

easiest with proving irrationality (assume its rational)

biconditional proofs

prove p→q and q→p

rational number

p/q where p and q are integers and q≠0

irrational number

one that is not rational

counterexample

an example that shows a statement is false

proofs using induction

1. state base case

2. inductive hypothesis: assume with variable k P(k)

3. inductive step: "we want to show that _______ " P(k+1)

4. use hypothesis (do some math) to show statement is true for k+1

5. conclusion: "by induction..."

growth of functions

constants

log(n) where y=log(x) = base^y=x

linear n

quadratic n^2

exponential #^n

factorial n!

exponentiation n^n

highest order term

f(n) = O(g(n))

if for large enough n, f(n) is not more that a multiple of g(n)

eventually f does not grow faster than g."

f(n) = O(g(n)) if there exist numbers c and k such that if n>k, then f(n)≤Cg(n)

e.g. 3n^3 + logn - 7 + 2^n

O=(2^n)

relation

a relation between X and Y is any subset R⊆X×Y

reflexive

a relation on X is reflexive if every element of X is paired with itself

every element of X is paired with itself- loop at every point

antireflexive

no element is paired with itself- no loops

diagonal relation

∆ = {(x,x) | x ∈ X}

the smallest reflexive relation on X

any relation union the diagonal will be reflexive

symmetric

a relation R is symmetric xRy means yRx

(1,2) and (2,1)

loops and double arrows only/if A=A^t

antisymmetric

R is antisymmetric if xRy and yRx means x=y

the only symmetries occur on∆

no double arrows

transitive

a relation is transitive if whenever xRy and yRz, then xRz

(a, b), (b, c), (a, c)

single edge between X1 and Xn wherever it has a path

digraphs

a pair (X, E) where X is any set and E is a set of ordered pairs from X.

X is the vertex set

E is the edge set

matrices

A= [aij] to refer to the matrix A whose element is in the ith row and jth column is aij

a mxn matrix has m rows and n columns

transpose

matrix A^t = [aji]

the rows and columns were exchanged

Addition and Subtraction of matrices

A±B = [aij ± bij]

Scalar multiplication

cA = [c*aij]

dot product

of a 1xm matrix A and an mx1 matrix B

matrix multiplication

mxk matrix A and kxn matrix B is the matrix mxn

the entry of AB in the ith row and the jth column is the dot product of the ith row of A and the jth column of B.

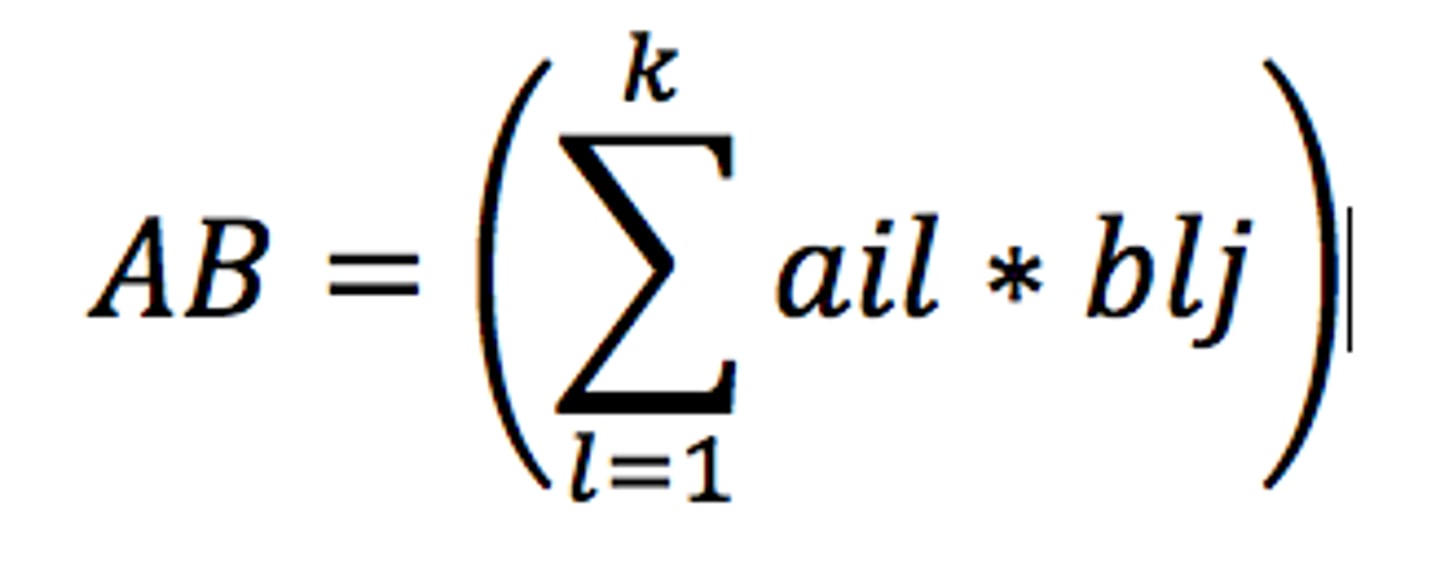
matrix multiplication ex

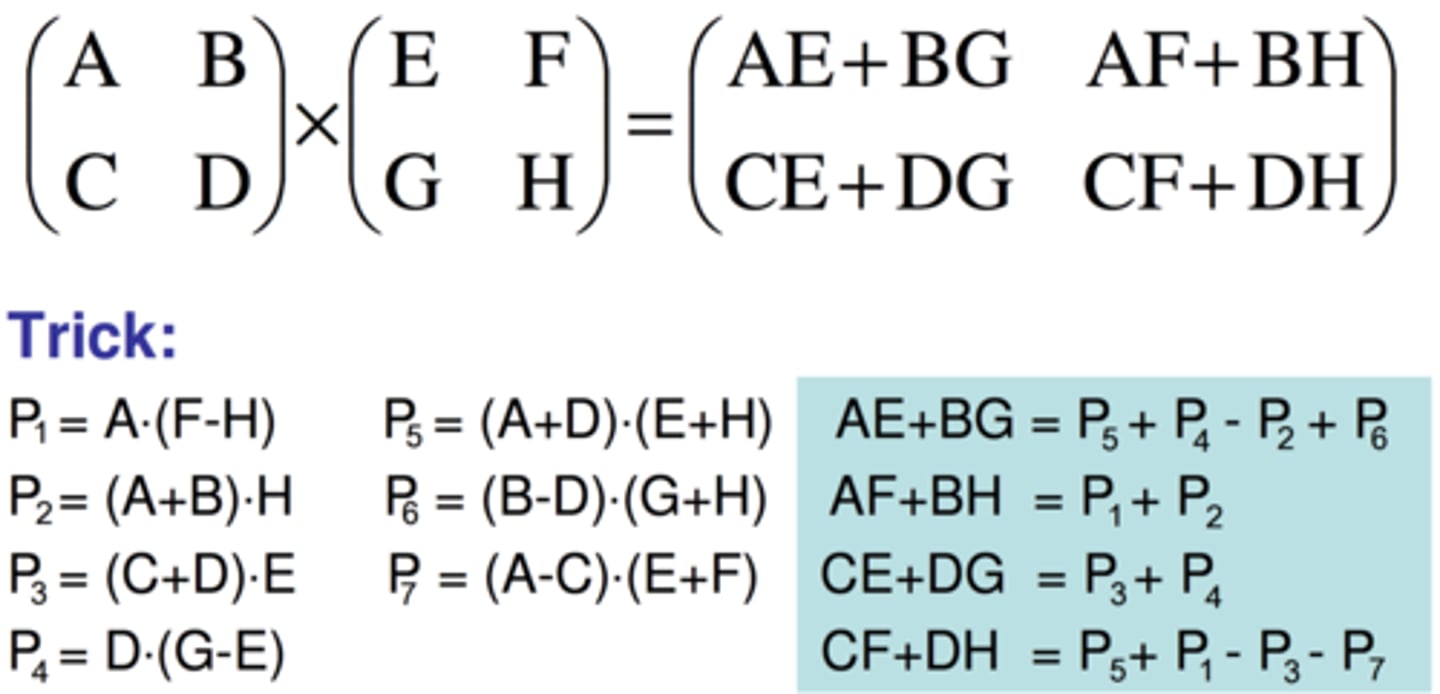
identity matrix

matrix In where the diagonal is all 1s and the rest are all 0s

Boolean Matrix

a matrix whose entries are all bits (1 or 0)

can be combined using conjunct and disjunct (or/and)

bit

an element of the set {0, 1} where 0 represents a false statement and 1 represents a true statement

boolean dot product

A⨀B is (a_11∧b_11 )∨(a_12∧b_21 )... = 1 or 0

Boolean product

of a mxk boolean matrix A with a kxn Boolean matrix B is the mxn matrix A⨀B whose (i, j) entry is the boolean dot product of the ith row of A and the jth column of B.

where ever there is a 1 in the same place in A and B, there will be a 1 in the product, otherwise it is a 0.

closure

the smallest set containing X for which P is true

close with refelxiveness, symmetry, transitivity

compostition

of R with S is the relation

(S∘R)↔RS={(a,c)┤|∃ b such that aRb and bSc}

two statements are equivalent if

they are always true together or false together

p∨q ≡ ¬p→q

equivalence relation

is any relation that is reflexive, symmetric, and transitive

φ≡ψ,ψ≡Γ then φ≡Γ

equivalence class

of x ∈ X is [x]= {y|y∈X and xRy}

so [a]=[b]={a, b}

[c]=[d]=[e]={c, d, e}

one element from the set represents the entire set

partitions

a family of disjoint subsets P1, P2, P3,... ,Pn where Pi∩Pj=∅ and

P1∪P2∪P3∪... ∪Pn = X

partial orders

is a relation R is a partially ordered set or poset (X, ≤_R)

generalize ≤

reflexive, antisymmetric, transitive

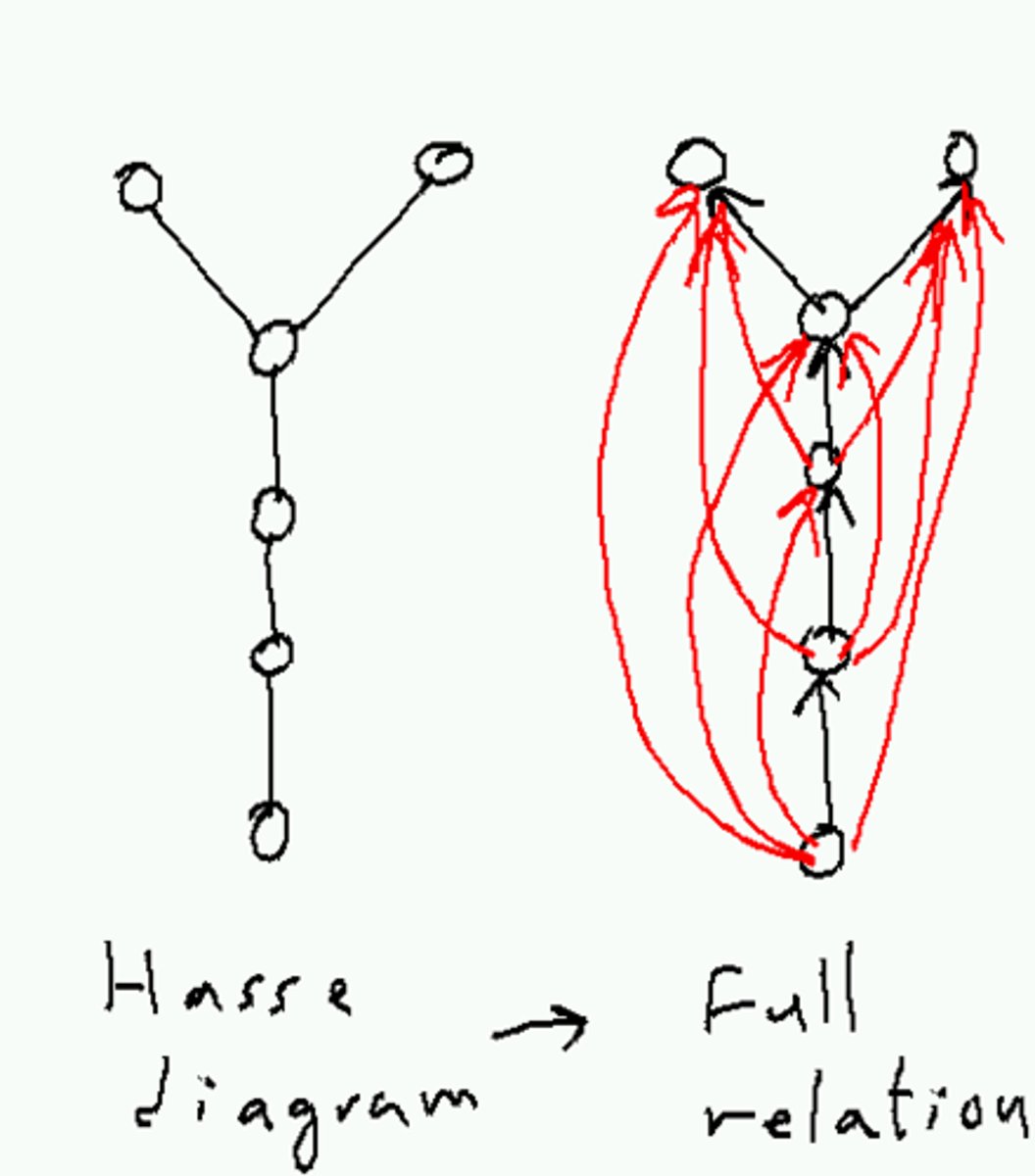
Hasse Diagram

bottom to top, removes clutter and captures flow

take the digraph of poset (X, ≤_R) and:

remove arrows, read edges bottom to top

remove all loops

if an edge connects x and y, y and z, remove the edge between x and z

comparable

two elements x, y of a poset if

X ≤_R Y or Y ≤_R X

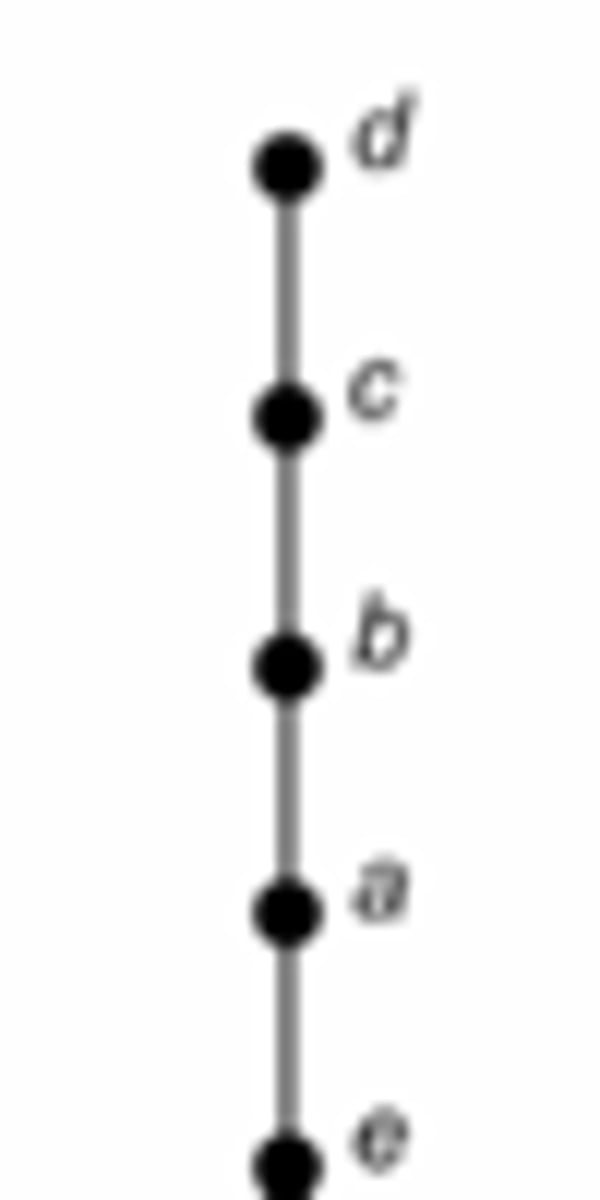
chain

a poset in which any pair of elements is comparable

maximal

if X ≤_R Y for no other y∈X

on hasse there is nothing above it

a single element=maximum

minimal

if Y ≤_R X for no other y∈X

on hasse nothing below it

a single element= minimum

total order

linear partial order

structured like a chain

covers

y covers x if x is related to y and there is no y such that x is related to y which is related to z