STAT 164 - Probability Distributions SUMMARY CHAPTER 2

• BERNOULLI

• BINOMIAL

• GEOMETRIC

• NEGATIVE BINOMIAL

• HYPERGEOMETRIC

• POISSON

• MULTINOMIAL

What are the types of DISCRETE DISTRIBUTIONS?

BERNOULLI

RANDOM EXPERIMENT

One trial with only two outcomes: success or failure

BERNOULLI

RANDOM EXPERIMENT

The probability of success is equal to p and the probability of failure is 1 - p

BERNOULLI

RANDOM VARIABLE (X)

Defined as 1 if a trial results in success and 0 if the same trial results in failure

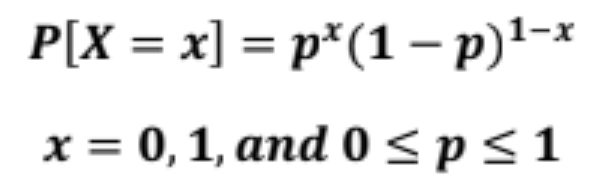
PROBABILITY FUNCTION

BERNOULLI

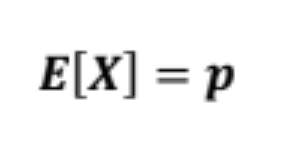
MEAN

BERNOULLI

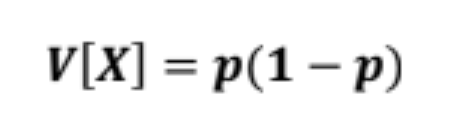
VARIANCE

BERNOULLI

DISTRIBUTION

BINOMIAL

BINOMIAL

RANDOM EXPERIMENT

The n identical Bernoulli trials are conducted independently, that is, the outcome of any one trial does not depend on the outcome of the other trial.

BINOMIAL

GEOMETRIC

RANDOM EXPERIMENT

The probability of success does not change from trial to trial

BINOMIAL

RANDOM EXPERIMENT

Sampling is with replacement

BINOMIAL

RANDOM VARIABLE (X)

Number of success/failures in n trials

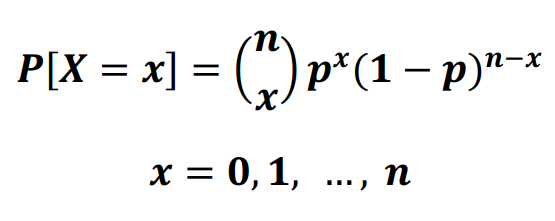
PROBABILITY FUNCTION

BINOMIAL

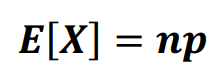
MEAN

BINOMIAL

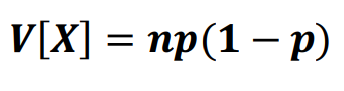
VARIANCE

BINOMIAL

DISTRIBUTION

GEOMETRIC

GEOMETRIC
HYPERGEOMETRIC

RANDOM EXPERIMENT

Each trial has two possible outcomes: success or failure

GEOMETRIC

RANDOM EXPERIMENT

The trials are independent.

GEOMETRIC

RANDOM VARIABLE (X)

• Number of trials to get the first success

• Number of trials BEFORE observing the first success

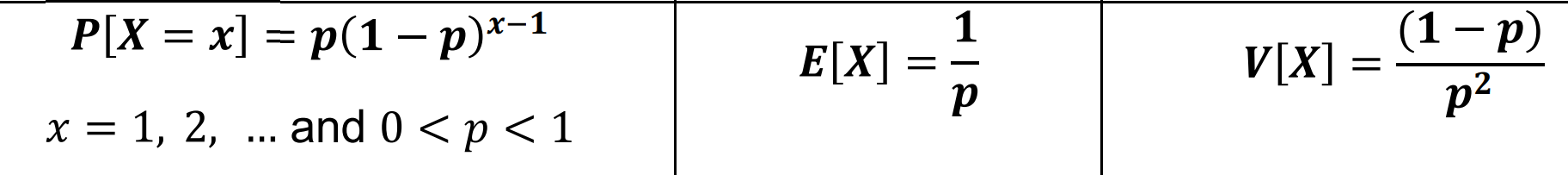
PROBABILITY FUNCTION, MEAN, and VARIANCE

given x = 1, 2, …….

GEOMETRIC

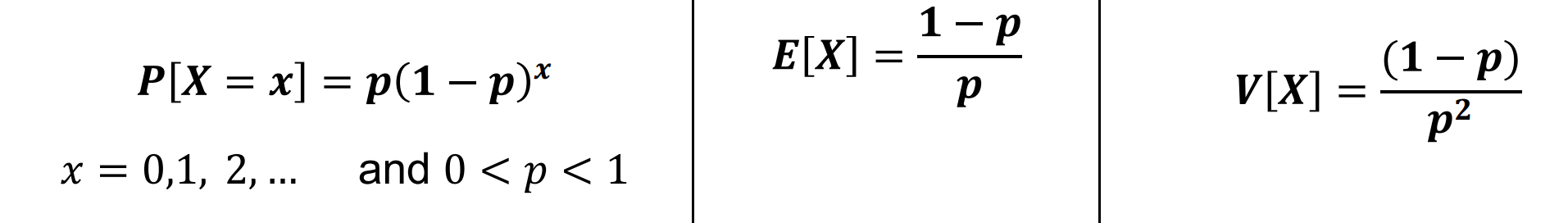
PROBABILITY FUNCTION, MEAN, and VARIANCE

given x = 0, 1, 2, …….

GEOMETRIC

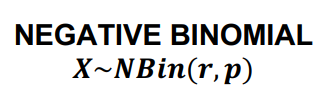
DISTRIBUTION

NEGATIVE BINOMIAL

NEGATIVE BINOMIAL

RANDOM EXPERIMENT

A generalization of the geometric distribution

NEGATIVE BINOMIAL

RANDOM VARIABLE (X)

Number of trials to get r successes

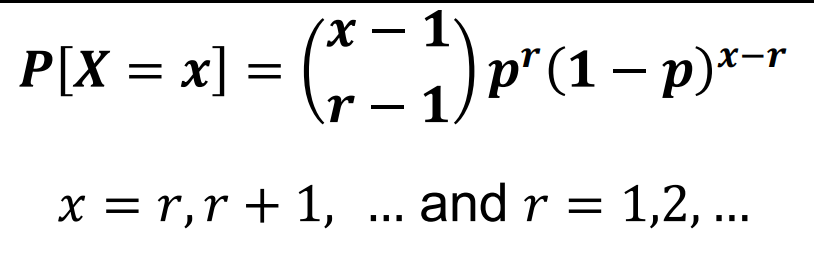
PROBABILITY FUNCTION

NEGATIVE BINOMIAL

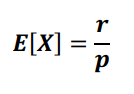
MEAN

NEGATIVE BINOMIAL

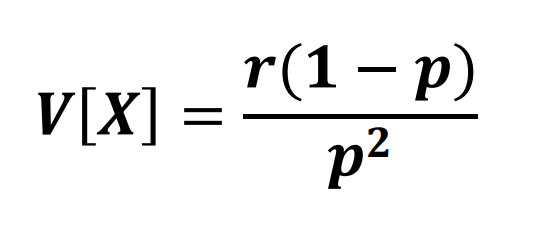
VARIANCE

NEGATIVE BINOMIAL

DISTRIBUTION

HYPERGEOMETRIC

HYPERGEOMETRIC

RANDOM EXPERIMENT

Sampling is without replacement

HYPERGEOMETRIC

RANDOM VARIABLE (X)

• Number of success/failures in n draws

OR

• Number of success/failures in a sample of size n

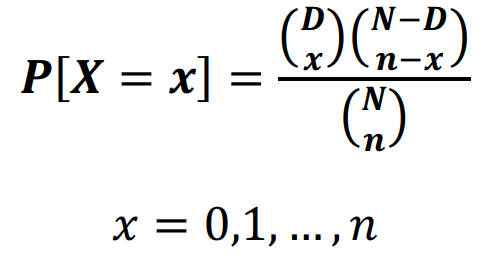
where N is the total number of objects, D is the number of success from N, and n is the number of objects drawn without replacement.

PROBABILITY FUNCTION

HYPERGEOMETRIC

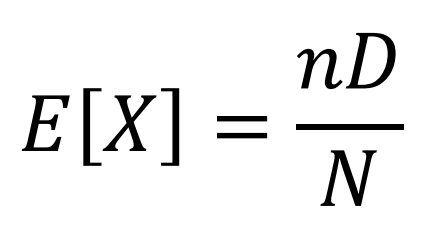
MEAN

HYPERGEOMETRIC

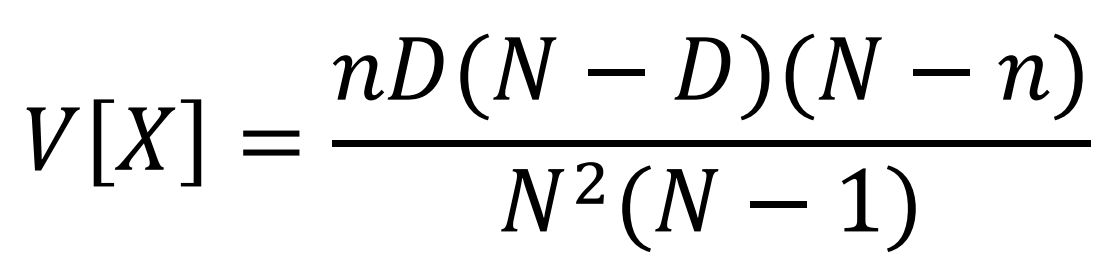
VARIANCE

HYPERGEOMETRIC

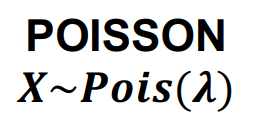
DISTRIBUTION

POISSON

POISSON

RANDOM EXPERIMENT

outcomes are discrete

POISSON

RANDOM EXPERIMENT

the number of successes, k, in any interval is independent of the number of successes in any other interval

POISSON

RANDOM EXPERIMENT

the chance of success is extremely small

POISSON

RANDOM VARIABLE (X)

Number of success/failure/events in a unit of time or space or interval

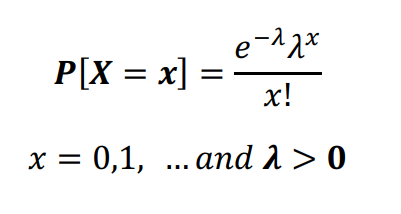
PROBABILITY FUNCTION

POISSON

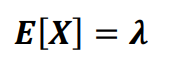
MEAN

POISSON

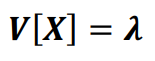
VARIANCE

POISSON

MULTINOMIAL

RANDOM EXPERIMENT

an event with k different outcomes, each of which is observed n_i times in N trials

MULTINOMIAL

RANDOM VARIABLE (X)

(one random variable per outcome) e.g. 1st outcome X₁= number of 1^st outcome in n trials

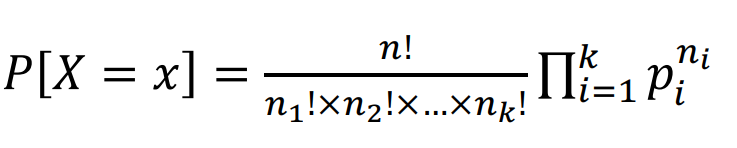
PROBABILITY FUNCTION

MULTINOMIAL

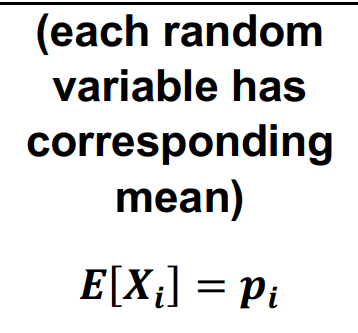
MEAN

MULTINOMIAL

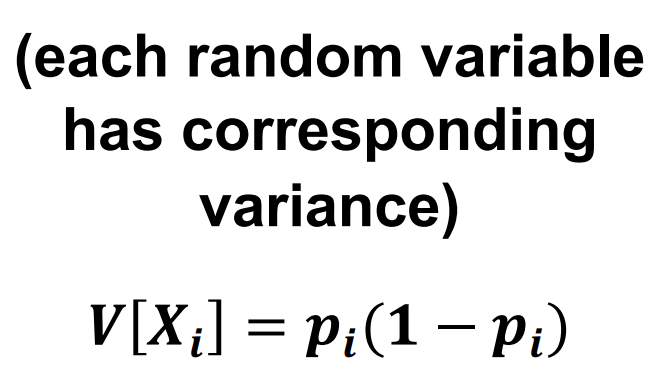
VARIANCE

MULTINOMIAL

• NORMAL

• STANDARD NORMAL

• EXPONENTIAL

What are the types of CONTINUOUS DISTRIBUTIONS?

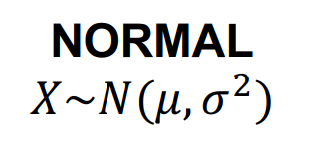
DISTRIBUTION

NORMAL

NORMAL

Its curve is bell-shaped and unimodal

NORMAL

Mean = Median = Mode

NORMAL

Symmetric about the mean

NORMAL

50% of the values are less than the mean and 50% are greater than the mean

NORMAL

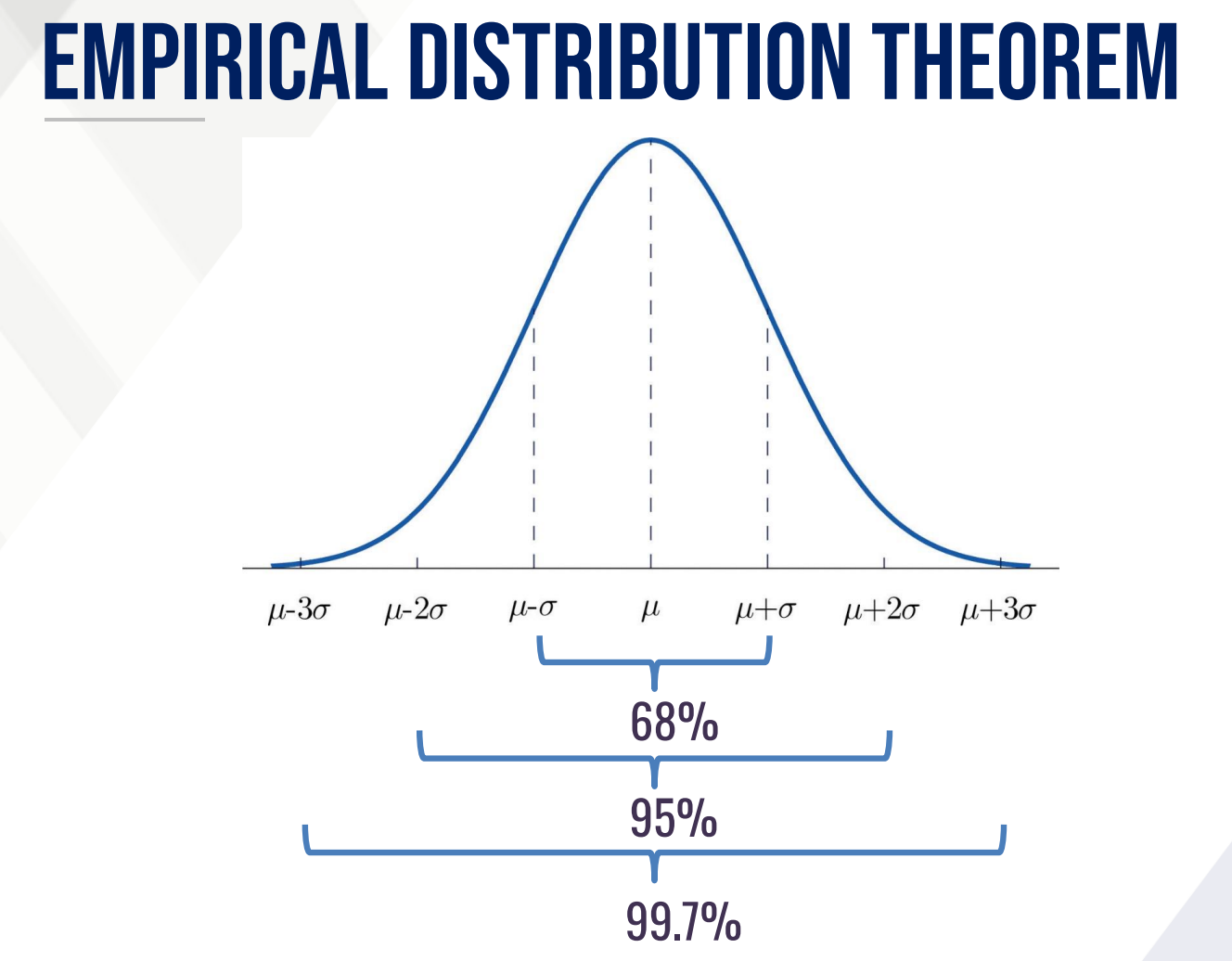
Empirical Distribution Theorem

• Approximately 68% of the data falls within one standard deviation from the mean

• Approximately 95% of the data falls within two standard deviation from the mean

• Approximately 99.7% of the data falls within three standard deviation from the mean

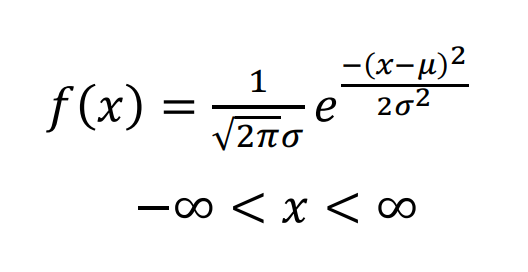
PROBABILITY FUNCTION

NORMAL

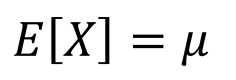
MEAN

NORMAL

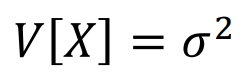
VARIANCE

NORMAL

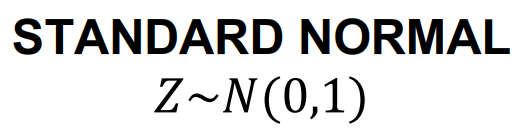
DISTRIBUTION

STANDARD NORMAL

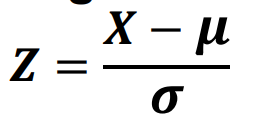
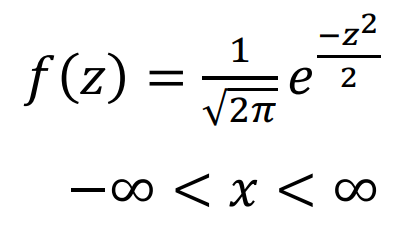
PROBABILITY FUNCTION

STANDARD NORMAL

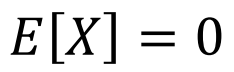
MEAN

STANDARD NORMAL

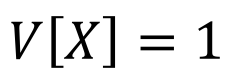
VARIANCE

STANDARD NORMAL

λ = 1/λ

DISTRIBUTION

EXPONENTIAL

EXPONENTIAL

The continuous counterpart of the geometric distribution

EXPONENTIAL

The only parameter is the failure rate, λ which is constant

EXPONENTIAL

Appropriate for modelling life length data, survival time, or time between Poisson events

EXPONENTIAL

The probability decreases over time at a constant rate

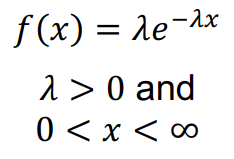
PROBABILITY FUNCTION

EXPONENTIAL

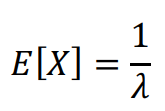
MEAN

EXPONENTIAL

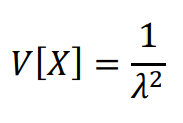
VARIANCE

EXPONENTIAL

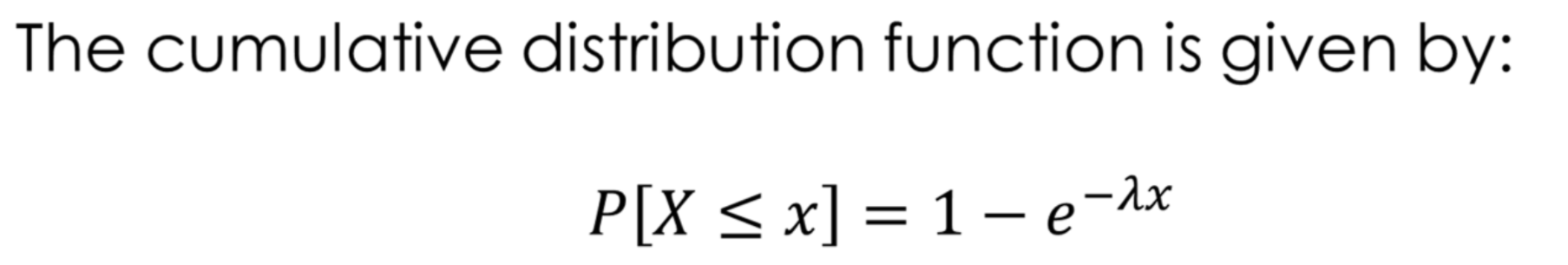
The cumulative distribution function of an EXPONENTIAL distribution is given by: