data science midterm

individuals

the objects described by our data (observations, population units)

variable

any attribute of an individual, can take on different values for different individuals 

• categorical - can take on fixed number of labels, assigns each individual to a particular group or category based on a quantitative property (ex: favourite colour, introversion type)

• quantitative - takes on numerical values, measures or counts something (ex: a person’s height, weight)

pie chart (categorical)

represents a categorical variable, telling us what values it takes and how often it takes them

• Each slice’s angle or area shows the relative frequency (%) for a category.

• Categories must be mutually exclusive and exhaustive, totaling 100%; otherwise, a pie chart is inappropriate.

bar chart (categorical)

consists of bars whose heights represent the proportion/frequency of values for each category

• can be used to visualize data that doesn’t add up to 100% as the y-axis is quantitative and the x-axis is categorical (bars provide measure of the categories)

histograms (quantitative)

A histogram is a graphical display of a quantitative variable using adjacent bars to show the frequency (%) of values within each interval (bin).

• It approximates the variable’s density, and as the number of bins increases (with narrower widths), it approaches a smooth density curve representing the overall distribution pattern.

overall pattern of histograms

Center (location): the mean or median.
Shape: symmetry or skewness.

• Symmetric: left and right sides are mirror images.

• Right-skewed: right tail (larger values) extends farther; mean > median.

• Left-skewed: left tail (smaller values) extends farther; mean < median.
  Variability (spread): measured by variance, standard deviation, range, or IQR.
  Deviations (outliers): observations that break the overall pattern.

stemplot (quantitative)

a graphical display of quantitative data that uses the actual digits of the observations to help convey the distribution of the data 

• you can determine the shape of a distribution from a stemplot by observing the symmetry, skewness, number of peaks, and any gaps or outliers in the data 

timeplot (quantitative)

a graphical display of a quantitative variable against time

• time is always on the x-axis, each point represents a value at a specific time

• useful for identifying trends, cycles, and patterns

mean

the sum of the values divided by the number of values

median

the midpoint of the distribution

1. order values from least to greatest

2. if n is odd, the median is the middle value

3. if n is even, the median is the average of the 2 middle values 

measures of central tendency

tells us about the typical or average value in a dataset 

mode

most frequently occurring value in the dataset

measuring variability: the quartiles

• Q1 (first quartile) - the median of the lower half

• Q2 (second quartile) - overall median

• Q3 (third quartile) - median of the upper half

five-number summary

consists of 5 key values that provide a concise overview of its distribution

• minimum (smallest value in the dataset)

• Q1, Q2, Q3

• maximum (largest value)

box and whisker plot

a graphical representation of the five-number summary

1. draw box from Q1 to Q3

2. mark median (Q2) inside the box

3. whiskers to min and max 

interquartile range

a measure of statistical dispersion

• calculated by Q3 - Q1 = IQR

inner fence

the interval (Q1 - 1.5 x IQR, Q3 + 1.5 x IQR)

• any observation that falls outside of this interval is considered an outlier

modified boxplot

extends whiskers only to the most extreme values within the inner fence, with outliers plotted as individual points beyond the whiskers 

variance

a measure of how much the values in the dataset vary/spread out from the mean

standard deviation

the square root of the variance, provides measure of spread in the same unit as data 

choosing measures of centre and variability

2 options - mean and standard deviation or five-number summary

• use mean and standard deviation for symmetrical distributions without outliers

• use five-number summary for skewed distribution or if extreme outliers are present

density curve

A density curve f(x)is a smooth function where f(x)≥0 for all x (the curve lies on or above the x-axis).

• The total area under the curve equals 1.

• It can be used to compute probabilities.

• The mean (μ) is the balance point of the curve.

• The median (m) divides the area under the curve into two equal halves.

• The mode is the point where the curve reaches its maximum height.

population

the target collection of individuals of interest

parameter

a numeric description of an attribute of the population

sample

a subset of the population which is available to collect data from

statistic

a numeric summary/description of the sample

normal distribution

A normal distribution is a common, bell-shaped distribution found in many statistical and real-world phenomena.

• Notation: N(μ,σ) — mean μ, standard deviation σ

• Shape: bell-shaped, symmetrical, with mean = median = mode

• Empirical Rule:

  • 68% of data within 1 standard deviation of the mean

  • 95% within 2 standard deviations

  • 99.7% within 3 standard deviations

cumulative proportion

of a value x in a distribution is the proportion of observations that are less than or equal to x

standard normal distribution

the normal standard distribution with mean 0 and standard deviation 1, denoted N(0,1)

standardization 

the process of transforming from a normal distribution to a standard distribution

• if x is an observations from a distribution that has mean μ and standard deviation σ, then the standardized value of x is z = x - μ / σ 

• to convert a z-score back to a raw score x = σ x z + μ   

scatterplot (quantitative)

a graphical display of the relationship between 2 quantitative variables measured on the same individuals

• each individual appears as a point on the plot

• x and y coordinates each give the value of different variables to the same individuals

response variable

measures the outcome of a study (y-axis)

explanatory variable

may explain or influence changes in the response variable (x-axis) 

interpreting scatterplots

when examining a scatterplot, looking for the following features:

• outliers - an individual that falls outside the overall pattern

• form - linear or non-linear

• direction - positive or negative association

• strength - how closely the points follow the form (strong, moderate, weak)

correlation r

measures the direction and strength of the linear relationship between 2 quantitative variables

• ranges from -1 to +1

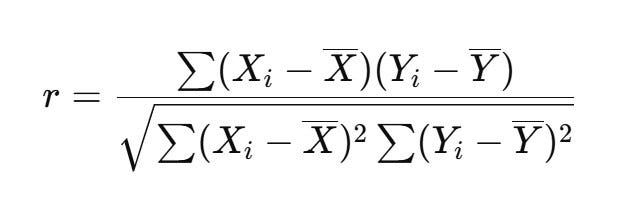
downsides to correlation

• correlation doesn’t imply causation (may be confounding variables at play)

• sensitivity to outliers

• limited to linear relationships 

• ignores other factors (variables not being studied)

regression line

a straight line that describes how a response variable y changes as an explanatory variable x changes

least squares regression line (line of best fit)

the line that minimizes the sum of the squared differences between the observed values and the values predicted by the line

• equation - ŷ = a + bx

• slope - b = r x Sy/Sx

• intercept - a = y -bx

coefficient of determination R²

measures the proportion of variance in the response variable explained by the explanatory variable 

• equation - R² = corr(x,y)² 

  • a value of 1 means the model perfectly predicts the outcome

  • a value of 0 means the model explains none of the variability in the outcome variable

residual

the difference between a response variable and its corresponding predicted value from the regression line

• equation - e = y - ŷ

residual plot

A residual plot helps assess whether a linear model fits the data well.

• Residuals should be randomly scattered around 0

• The spread of residuals should be consistent across all x-values

• There should be no visible curves or clusters

• Residuals should be roughly symmetric

influential observation

an observation which drastically impacts the slope/intercept of the regression line

• a datapoint has high leverage if its x-value is extreme to the rest of the points

lurking variable

an unobserved variable that influences both the explanatory and response variables, potentially leading to a spurious association between them

ecological fallacy

occurs when conclusions about individual behavior are drawn from group-level data.

It involves two main errors:

1. Assuming that a relationship observed for groups also applies to individuals within those groups.

2. Overestimating the strength of the relationship based on aggregated (group-level) data.

two-way table

describes 2 categorical variables by providing counts for each possible combination of a row variable and a column variable

marginal distribution

a variable describes the value that a specific variable takes irrespective of the other (only applies in the context of multiple variables)

conditional distribution

the probability distribution of a variable given that another variable has a specific value (separate conditional distribution for each value of the other variable)

probability, risk, and odds

• suppose x in some categorical variable and c is some category of x, the percent of individuals in category c is given b: # of individuals in category c / # of individuals in total x 100%

• the proportion, probability, and risk of individuals in category c is given by: # of individuals in category c / # of individuals in total

• the odds of category c given by: # of individuals in category c / # of individuals not in category c

relative risk (RR)

risk in 1 group (group 1) compared to the risk in another group (group 2 or baseline/reference)

• convention: in medical applications in which risk refers to the negative outcome (disease, death), the baseline group is the control group

• equation - RR = risk in group 1 / risk in group 2

properties of relative risk

• RR = 1 - both groups have equal risk

• RR > 1 - group 1 has higher risk than baseline

• RR < 1 - group 1 has lower risk than baseline

odds ratio (OR)

odds in one category (group 1) compared to the odds of another category (group 2)

• equation - OR = odds in group 1 / odds in group 2

properties of odds ratios

• OR = 1 - both groups have equal odds

• OR > 1 - group 1 has higher odds than baseline

• OR < 1 - group 1 has lower odds than baseline

simpson’s paradox

occurs when a trend that appears in different groups of data disappears or reverses when the groups are combined.

• This happens when a lurking variable (often a grouping variable) affects the relationship between two variables differently across subgroups. The overall aggregate data can show the opposite pattern from what is observed in each individual subgroups