Addendum CH 1 Derivatives (DONE)

Risk Neutral

• Being ”risk neutral” means being indifferent about risk.

• For example, suppose I flip a coin and offer you $100 if the coin lands on heads and $0. if you’re risk neutral, then you would value this as:

  • Expected payoff = ($100 x 50%) + ($0 x 50%) = $50

  • A risk neutral person is indifferent to whether this $50 comes from a guaranteed payout or a risky bet.

Risk Neutral Pricing

• Risk-neutral pricing refers to pricing assets as if investors were risk neutral. 

• It assumes investors only care about the expected payoff of an asset and not the risk involved.

• In reality, people have varying levels of risk aversion. Risk-neutral pricing allows us to compute the “fair” value of an asset by assuming everyone is risk neutral. 

• Why? Because varying levels of risk = varying levels of risk premium = difficult to price asset

Risk Neutral Probability

• Risk-neutral probabilities are probabilities of potential future outcomes adjusted for risk, which are then used to compute expected asset values.

• In other words, securities are bought and sold as if the hypothetical fair, single probability for an outcome were a reality, even though that is not, in fact, the actual scenario.

• Implementing risk-neutral probability in pricing assets is useful because you are able to price an asset at its trade price when employing the risk-neutral measure.

•  A key assumption in computing risk-neutral probabilities is the absence of arbitrage. 

• The concept of risk-neutral probabilities is widely used in pricing derivatives.

Risk Neutrality and the Term Structure

• In a risk-neutral world, the term structure reflects only expected future short-term rates.

• In reality, the shape of the term structure is influenced by both expectations and risk premiums.

• Risk-neutral pricing helps isolate expectations, making it easier to analyze and compare with real-world observations.

The term structure of interest rates is a comparison of market yields on securities, assuming all characteristics except maturity are the same

• Change in required interest rates as the maturity of a security changes is called the maturity premium (MP)

• The MP can be positive, negative, or zero 

The following general equation can be used to determine the factors that functionally impact the fair interest rate (ij*) on an individual (jth) financial security:

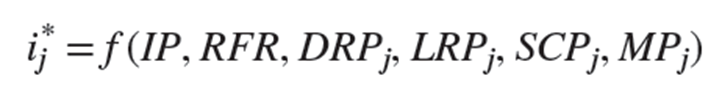
•IP = Inflation premium

•RFR = Real risk-free rate

•DRPj = Default risk premium on the jth security

•LRPj = Liquidity risk premium on the jth security

•SCPj = Special feature premium on the jth security

•MPj = Maturity premium on the jth security

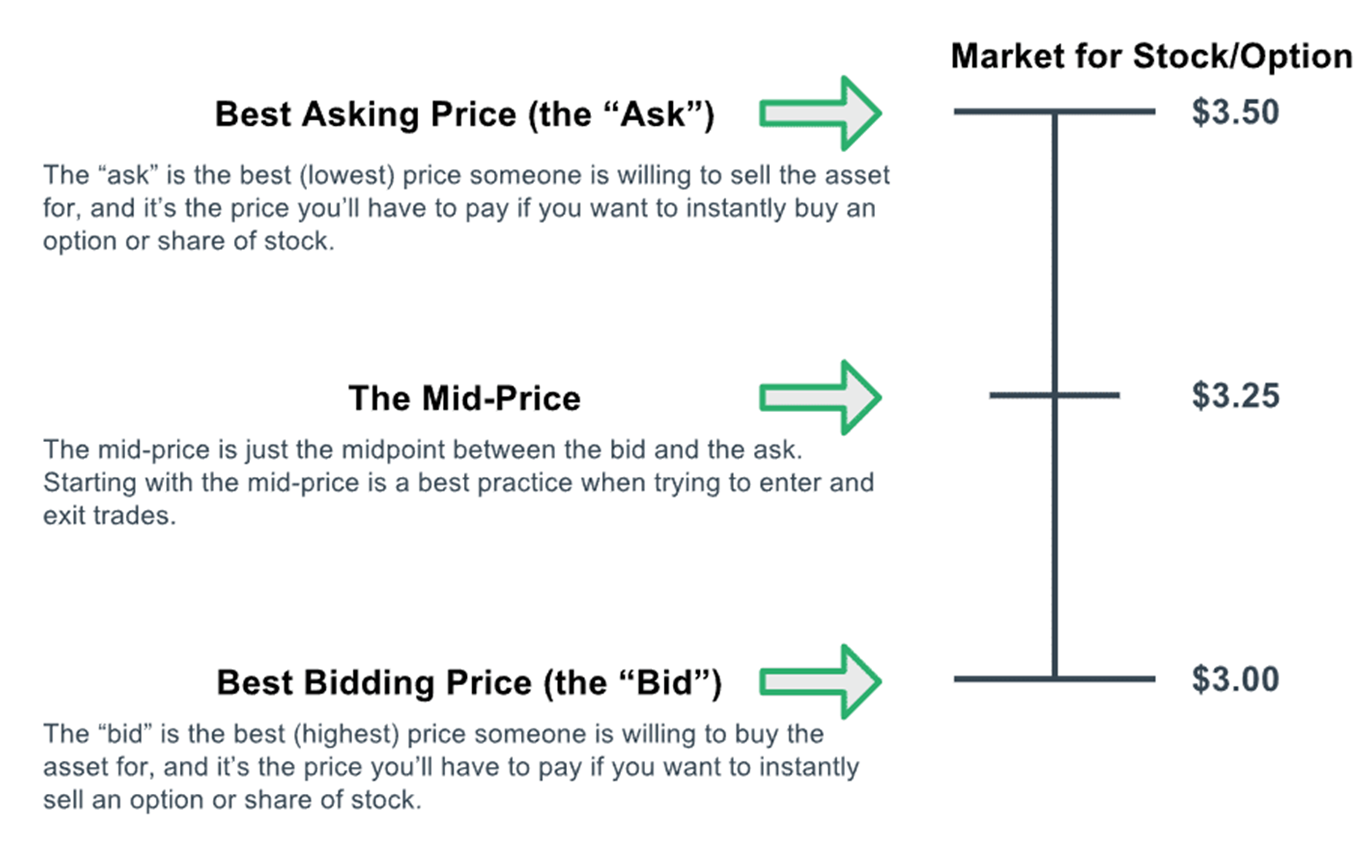
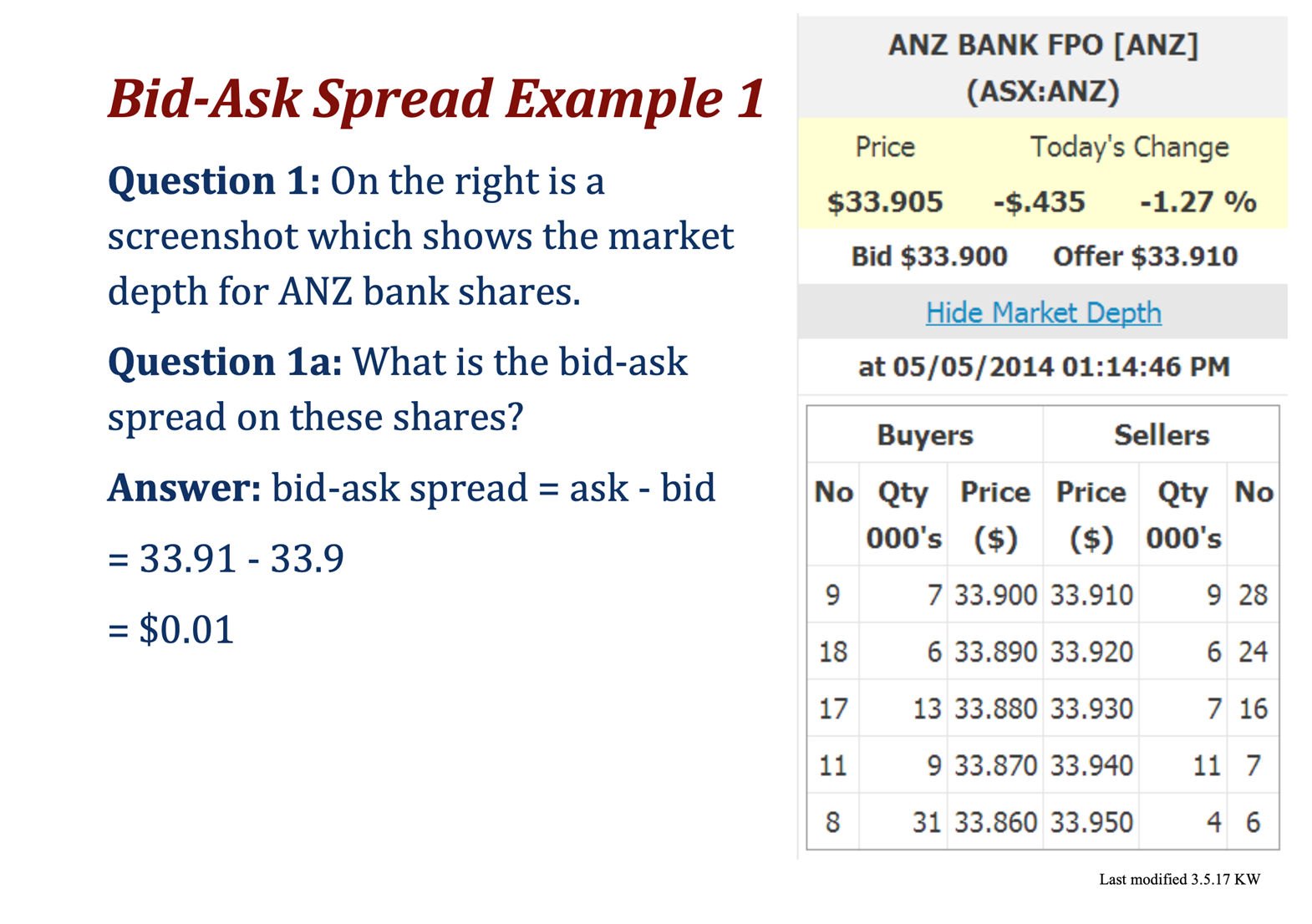
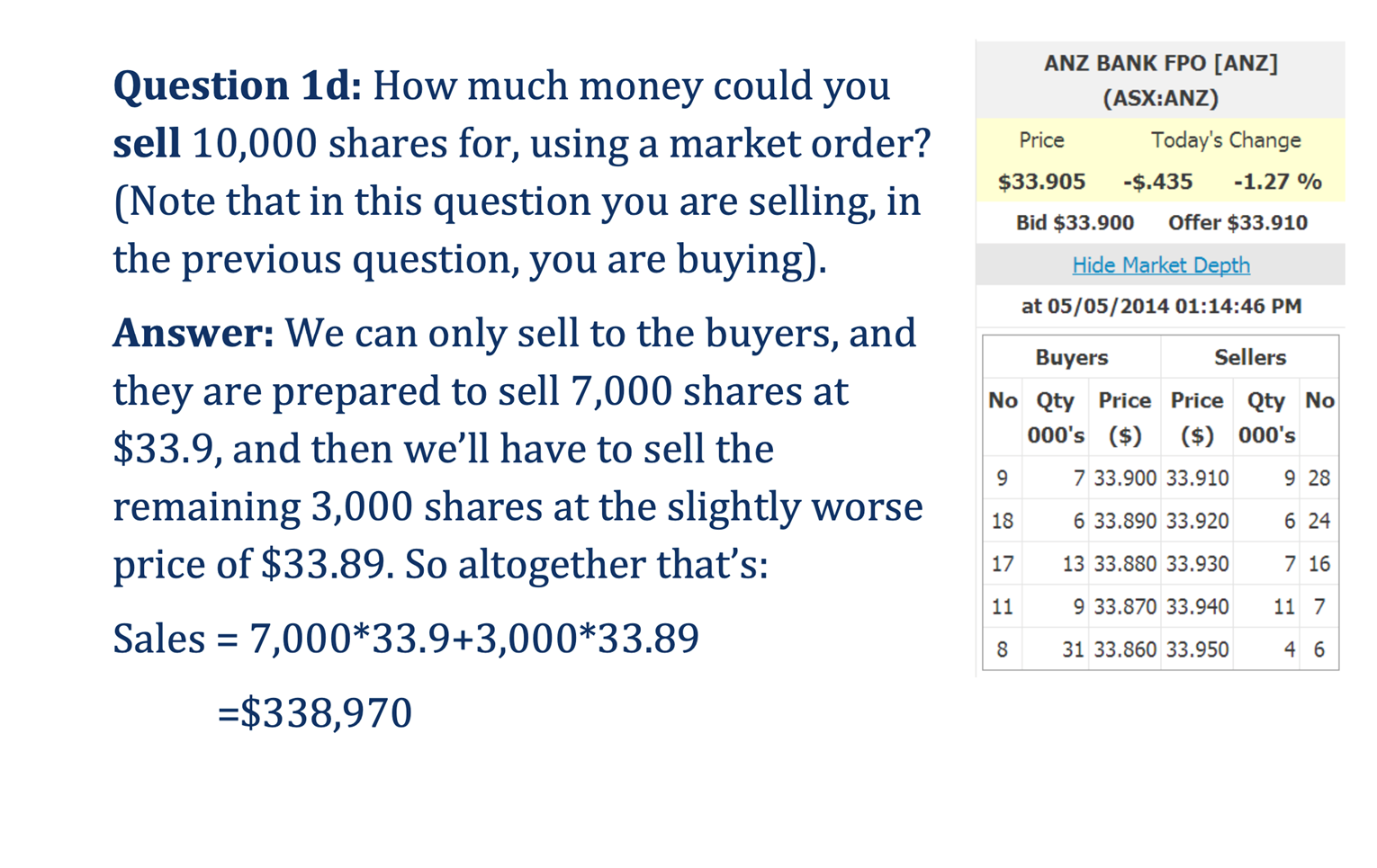
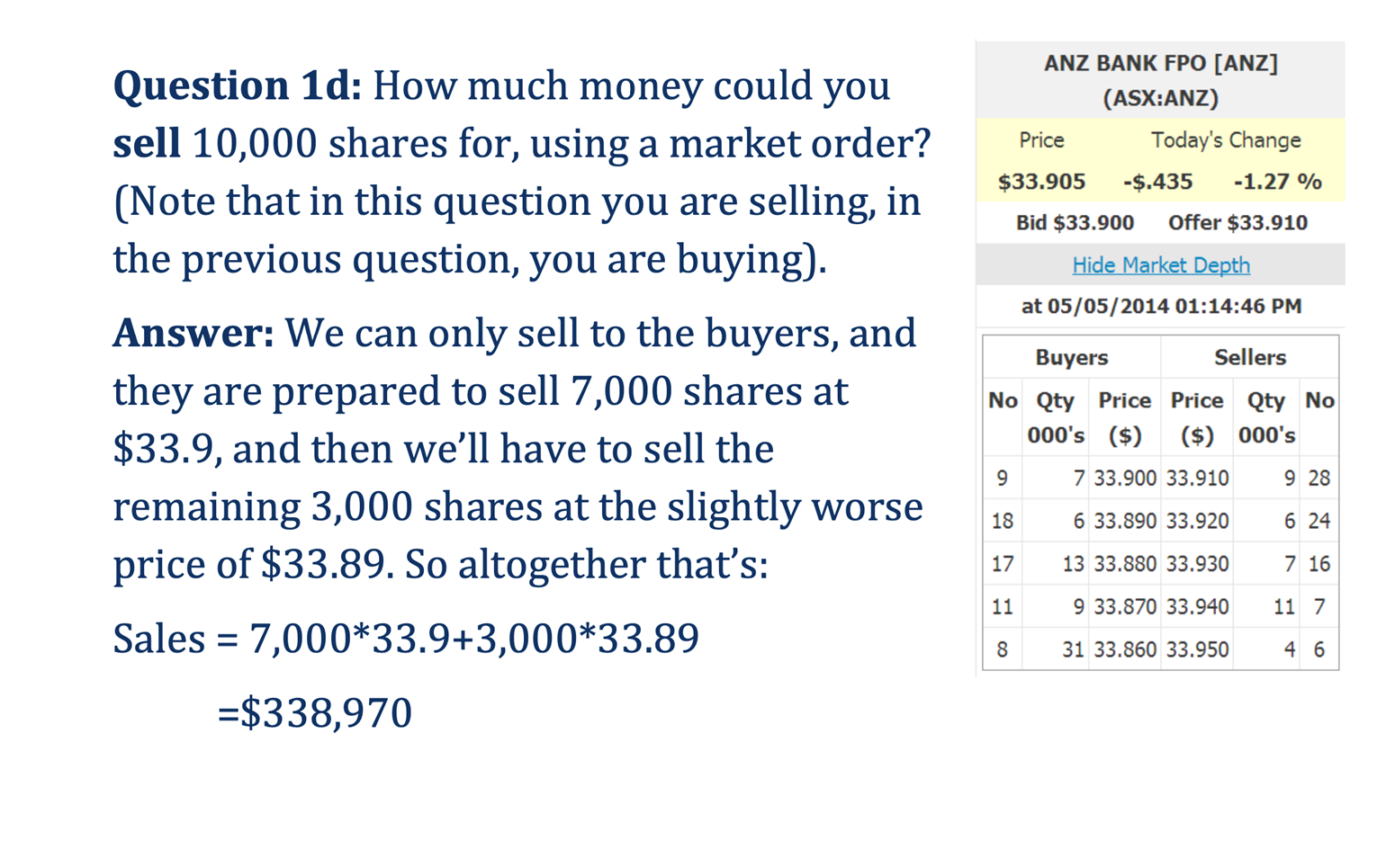
Bid-Ask Spread

• You want to buy on the bid & sell on the ask. The best ask will always be higher than the best bid.

• If you use limit orders, you’ll buy on the bid & sell on the ask (assuming your orders are executed). 

• However, if you use market orders, you will buy on the ask & sell on the bid.

• The danger of using limit orders is your order may not get executed due to price action.

• The danger of using market orders is slippage. 

If you use ____________, you’ll buy on the bid & sell on the ask (assuming your orders are executed).

limit orders

However, if you use ___________, you will buy on the ask & sell on the bid.

market orders

The danger of using limit orders is your order may not get executed due to ________.

price action

The danger of using market orders is __________.

slippage

Slippage

• Slippage refers to the difference between the expected price of a trade and the price at which the trade is executed. 

• Slippage can occur at any time but is most prevalent during periods of higher volatility when market orders are used. 

• It can also occur when a large order is executed but there isn't enough volume at the chosen price to maintain the current bid/ask spread.

• Slippage refers to all situations in which a market participant receives a different trade execution price than intended.

• Slippage occurs when the bid/ask spread changes between the time a market order is requested and the time an exchange or other market maker executes the order.

• Slippage occurs in all market venues, including equities, bonds, currencies, and futures.

• The final execution price vs. the intended execution price can be categorized as positive slippage, no slippage, or negative slippage.

• Slippage can be limited by not executing trades late in the day, investing in calm and liquid markets, and placing limit orders.

___________ can change quickly, allowing slippage to occur during the delay between a trade being ordered and when it is completed. 

Market prices

While a __________ prevents negative slippage, it carries the inherent risk of the trade not being executed if the price does not return to the limit level.

limit order

This risk increases in situations where market fluctuations occur more quickly, significantly limiting the amount of time for a trade to be completed at the ________________.

intended execution price

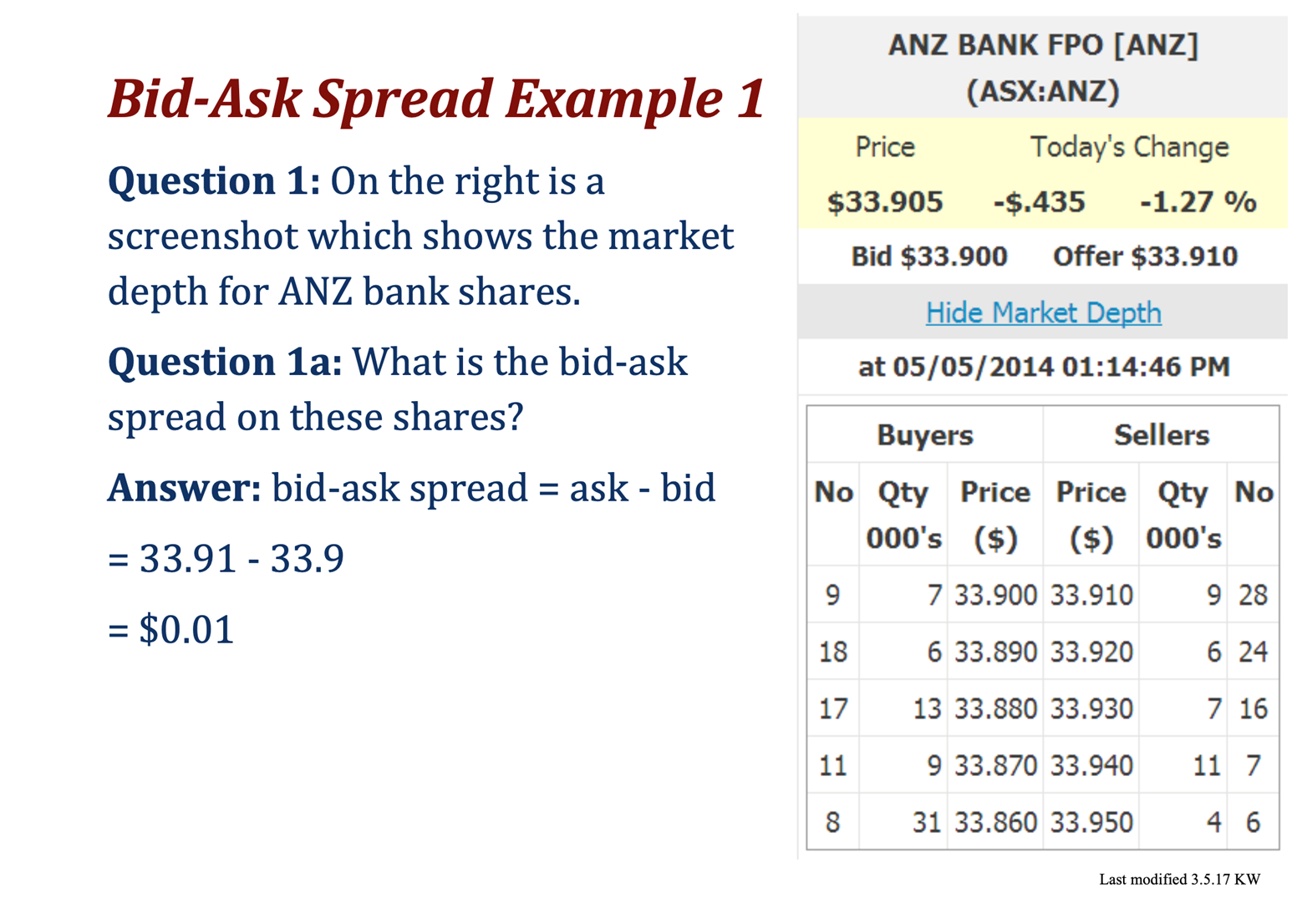
For example, say Apple's bid/ask prices are posted as $183.50/$183.53 on the broker interface. A market order for 100 shares is placed, with the intention the order gets filled at $183.53. 

However, micro-second transactions by computerized programs lift the bid/ask spread to $183.54/$183.57 before the order is filled. 

The order is then filled at $183.57, incurring $0.04 per share or $4.00 per 100 shares, which is negative slippage.

Volatility Measures

• Standard deviation: A measure of the dispersion of returns around the mean, indicating the total risk of an asset.

• Volatility: The degree of variation in an asset's price over time, typically measured by standard deviation.

• Variance: The squared deviation of returns from the mean, representing the overall risk of an asset.

• Covariance: A measure of how two assets move together, indicating whether they tend to rise and fall in tandem.

_____________: A measure of the dispersion of returns around the mean, indicating the total risk of an asset.

Standard deviation

__________: The degree of variation in an asset's price over time, typically measured by standard deviation.

Volatility

___________: The squared deviation of returns from the mean, representing the overall risk of an asset.

Variance

______________: A measure of how two assets move together, indicating whether they tend to rise and fall in tandem.

Covariance

Derivative Securities

• A derivative is a financial security that derives its value based on an underlying asset.

• The underlying asset can be a commodity, a security, a real asset, an interest rate, an index, volatility, etc.

• Many different types of derivative securities exist (forwards, futures, options, options on futures, swaps, etc.)

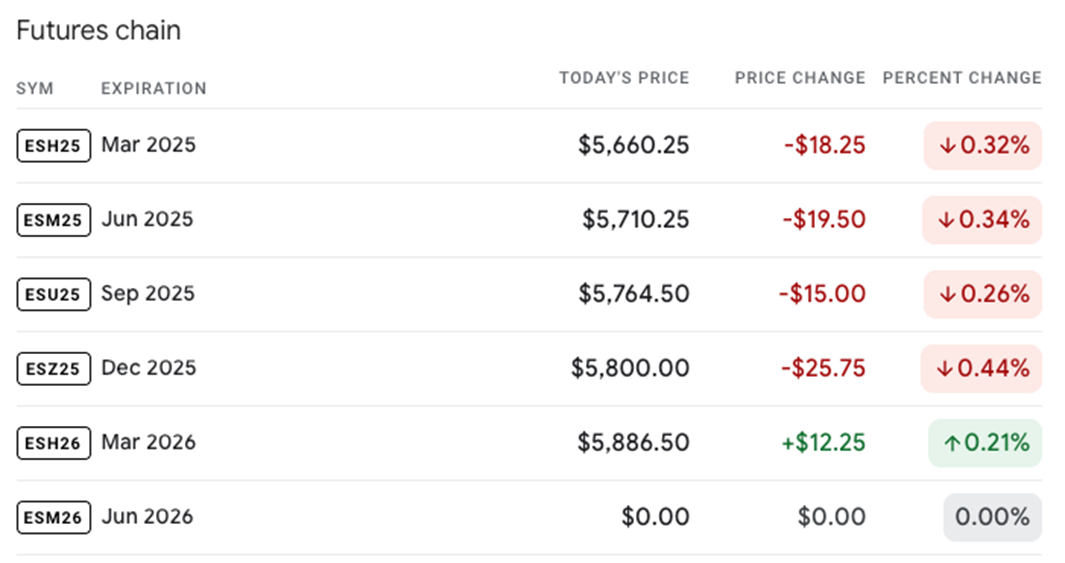
Spot price vs Forward price

• The spot price is the current price of an asset

• The forward price is a future price of an asset

  • There are multiple forward prices for an asset depending on the maturity

  • For example, the spot price of the S&P 500 is $5,660.25, and maturities, starting with the March expiry, are priced as follows: 

The ____________ is the current price of an asset

spot price

The _______________ is a future price of an asset

forward price

Spot price vs Forward price

Forward contracts vs Futures contracts

• Forward contracts are non-standardized (customizable), do not trade on exchanges (traded OTC), and are not cleared through a clearinghouse

• Futures are standardized, do trade on exchanges (and are thus marked-to-market daily and traders are subject to margin requirements), and are cleared through a clearinghouse

• While forward contracts are not cleared through a clearinghouse, certain other OTC derivatives, such as interest rate swaps and credit default swaps, are cleared through a clearinghouse (post Dodd-Frank)

_______________ are non-standardized (customizable), do not trade on exchanges (traded OTC), and are not cleared through a clearinghouse

Forward contracts

_____________ are standardized, do trade on exchanges (and are thus marked-to-market daily and traders are subject to margin requirements), and are cleared through a clearinghouse

Futures

While forward contracts are not cleared through a clearinghouse, certain other OTC derivatives, such as interest rate swaps and credit default swaps, are cleared through a ___________ (post Dodd-Frank)

clearinghouse

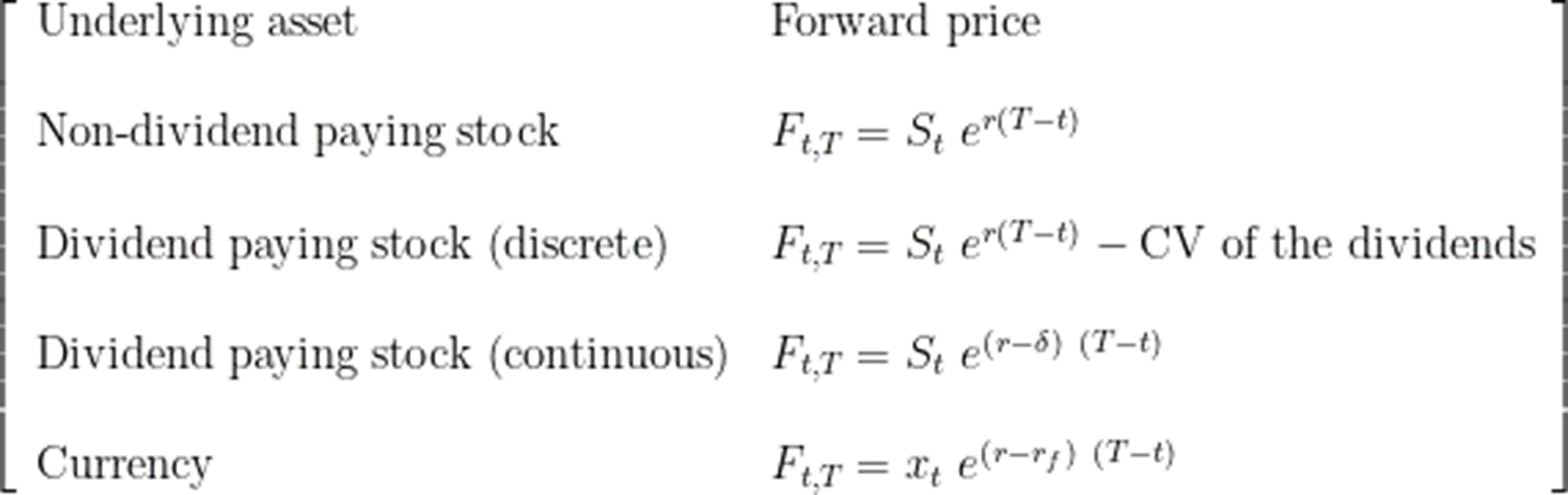
• Every futures contract has an underlying asset, the quantity of the asset, delivery location, and delivery date. 

• For example, if the underlying asset is light sweet crude oil, the quantity is 1,000 barrels, the delivery location is the Henry Hub in Erath, Louisiana and the delivery date is December 2017.

• When a party enters into a futures contract, they are agreeing to exchange an asset, or underlying, at a defined time in the future. This asset can be a physical commodity like crude oil, or a financial product like a foreign currency.

• When the asset is a physical commodity, to ensure quality, the exchange stipulates the acceptable grades of the commodity.

• For example, WTI Crude Oil contracts at CME Group is for 1,000 barrels of a grade of crude oil known as “light, sweet” which refers to the amount of hydrogen sulfide and carbon dioxide the crude oil contains.  

• When the asset is a physical commodity, to ensure quality, the exchange stipulates the acceptable grades of the commodity.

• For example, WTI Crude Oil contracts at CME Group is for 1,000 barrels of a grade of crude oil known as “light, sweet” which refers to the amount of hydrogen sulfide and carbon dioxide the crude oil contains.  

• Futures contracts for financial products are understandably more straightforward: the U.S. dollar value of 100,000 Australian dollars is the U.S. dollar value of 100,000 Australian dollars.

• Each futures contract specifies is the quantity of the product delivered for a single contract, also known as contract size. For example: 5,000 bushels of corn, 1,000 barrels of crude oil or Treasury bonds with a face value of $100,000 are all contract sizes as defined in the futures contract specification.  

• All futures contracts have a specified date on which they expire (typically the 3^rd Friday of the month). Prior to the expiration date, traders have a number of choices to either close out or extend their open positions (roll over) without holding the trade to expiration, but some traders will choose to hold the contract and go to settlement.

• Settlement is the fulfillment of the legal delivery obligations associated with the original contract. For some contracts, this delivery will take place in the form of physical delivery of the underlying commodity. 

• For example, a food producer looking to acquire grain may be looking to take delivery of physical corn or wheat, and a farmer may be looking to deliver his grain to that producer. 

• Although physical delivery is an important mechanism for certain energy, metals and agriculture products, only a small percent of all commodities futures contracts are physically delivered.

• All futures contracts have a minimum price fluctuation also known as a tick. Tick sizes are set by the exchange and vary by contract instrument.

• For example, the tick size of an E-Mini S&P 500 Futures Contract is equal to one quarter of an index point. Since an index point is valued at $50 for the E-Mini S&P 500, a movement of one tick would be  .25 x $50 = $12.50

• The tick size of the NYMEX WTI Crude Oil contract is equal to 1 cent and the WTI contract size is 1,000 barrels.  Therefore, the value of a one tick move is $10.

Contract Unit

• The contract unit is a standardized size unique to each futures contract and can be based on volume, weight, or a financial measurement, depending on the contract and the underlying product or market.

• For example, a single COMEX Gold contract unit (GC) is 100 troy ounces, which is measured by weight.

• A NYMEX WTI Crude Oil contract unit (CL) is 1,000 barrels of oil, measured by volume.

• The E-mini S&P 500 contract unit (ES) is a financial calculation based on a fixed multiplier times the S&P 500 Index.

______________, also known as contract value, is the financial expression of the contract unit and the current futures contract price.

Contract notional value

Assume a Gold futures contract is trading at price of $1,000. The notional value of the contract is calculated by multiplying the contract unit by the futures price.

• Contract unit x contract price = notional value

• 100 (troy ounces) x $1,000 = $100,000

If WTI Crude Oil is trading at $50 dollars and the contract unit is 1000 barrels, the notional would be:

• $50 x 1,000 = $50,000

Now assume E-mini S&P 500 futures are trading at 2120.00. The multiplier for this contract is $50.

• $50 x 2120.00 = $106,000

Notional values can be used to calculate hedge ratios versus other futures contracts or another risk position in a related underlying market.

• Value at risk / notional value = hedge ratio

____________ is the unit that oversees trading on the exchange and guarantees all trades made by the exchange traders

Clearinghouse

Clearing

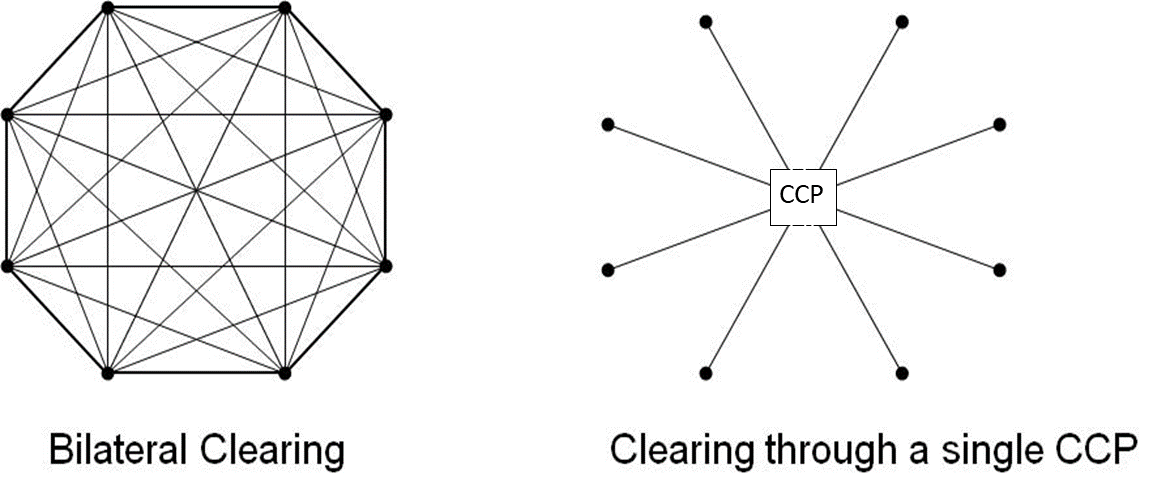
The clearinghouse breaks up every trade into a buy and sell transaction and takes the opposite side of the transaction, becoming the buyer for every futures contract seller and the seller for every futures contract buyer.

The clearinghouse breaks up every trade into a buy and sell transaction and takes the opposite side of the transaction, becoming the buyer for every futures contract seller and the seller for every futures contract buyer.

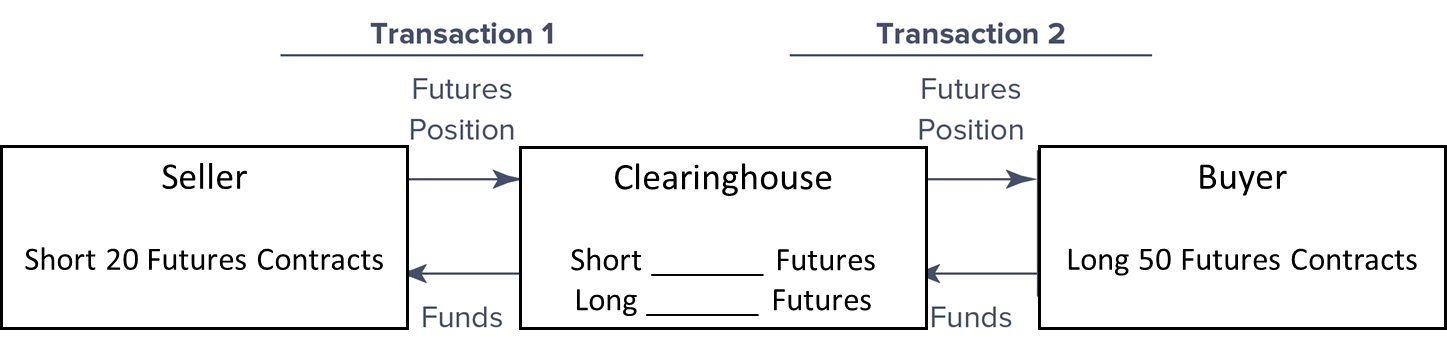
Short 50 Futures

Long 20 Futures

Participants in futures markets can be either _______________________

hedgers, speculators, or arbitrageurs

A ____________ vis any individual or firm that buys or sells the actual physical commodity. Many hedgers are producers, wholesalers, retailers or manufacturers and they are affected by changes in commodity prices, exchange rates, and interest rates.

hedger

A ___________ is any individual or firm that accepts risk in order to make a profit. Speculators can achieve these profits by buying low and selling high (or sell first and later buy at a lower price, i.e, being short)

speculator

Unlike speculators who assume market risk for profit, hedgers use the futures market to __________________.

manage and offset risk

An ____________is an individual or firm who attempts to profit from market inefficiencies. They seek to profit from the same asset being priced differently in separate markets by simultaneously buying the asset at a lower price and selling it at a higher price.

arbitrageur

There are several types of hedgers in the commodities markets:

• Buy-side hedgers, who are concerned about rising commodity prices (e.g., a jet fuel futures buyer at United Airlines)

• Sell-side hedgers, who are concerned about falling commodity prices (e.g., a corn farmer)

• Merchandisers, who both buy and sell commodities. Their risk is different than the directional risk of a traditional buying and selling hedger. Their risk is the spread or difference between the purchase and selling prices that determines their profitability.

_______________, who are concerned about rising commodity prices (e.g., a jet fuel futures buyer at United Airlines)

Buy-side hedgers

______________, who are concerned about falling commodity prices (e.g., a corn farmer)

Sell-side hedgers

____________, who both buy and sell commodities. Their risk is different than the directional risk of a traditional buying and selling hedger. Their risk is the spread or difference between the purchase and selling prices that determines their profitability.

Merchandisers

There are several types of speculators in the commodities markets:

• Portfolio/Investment Managers, who are responsible for investing or hedging the assets of a mutual fund, exchange-traded fund, or close-end fund.

• Hedge funds, which are managed portfolios of investments that use advanced investment strategies to maximize returns and are only open to qualified investors. 

• Proprietary trading firms (also called prop shops), which are similar to hedge funds but do not accept outside investor money (investors are partial owners of the firm. 

• Asset Managers (Commodity Trading Advisors), who manage investments for individuals specifically looking for exposure to commodities.

• Market makers, who are firms that have contractually agreed to provide liquidity to the markets.

• Individual traders, who trade their own money in their own accounts.

_____________________, who are responsible for investing or hedging the assets of a mutual fund, exchange-traded fund, or close-end fund.

Portfolio/Investment Managers

____________, which are managed portfolios of investments that use advanced investment strategies to maximize returns and are only open to qualified investors.

Hedge funds

__________________ (also called prop shops), which are similar to hedge funds but do not accept outside investor money (investors are partial owners of the firm.

Proprietary trading firms

________________ (Commodity Trading Advisors), who manage investments for individuals specifically looking for exposure to commodities.

Asset Managers

____________, who are firms that have contractually agreed to provide liquidity to the markets.

Market makers

__________________, who trade their own money in their own accounts.

Individual traders

Hedge Ratio

Suppose a portfolio manager has a $10,000,000 US equity market exposure. They want to hedge their market risk by selling E-mini S&P 500 futures contracts. The E-mini S&P 500 for the June expiry is trading at $5710.25 and the multiplier on the contract is 50. Using the hedge ratio, determine how many contracts they must sell to hedge their market risk.

• Contract unit x contract price = notional value

• Notional value = 50 x $5710.25 = $285,512.50

• Value at risk / notional value = hedge ratio

• $10,000,000 / $285,512.50 = 35.025

• If the portfolio manager sells 35 E-mini S&P 500 futures contracts against their long equity position, they have effectively hedged their market risk.

Calculating Futures Contract Profit or Loss

• Market participants trade in the futures market to make a profit or hedge against losses. 

• Each market calculates movement of price and size differently, and as such, traders need to be aware of how the market you are trading calculates profit and loss. 

• To determine the profit and loss for each contract, you will need to be aware of the contract size, tick size, current trading price, and what you bought or sold the contract for.

• Suppose you are trading WTI crude oil futures. One contract represents the expected value of 1,000 barrels of oil and the minimum tick size is $0.01

• If the current price of WTI futures is $54, the current value of the contract is determined by multiplying the current price of a barrel of oil by the size of the contract. In this example, the current notional value would be $54 x 1000 = $54,000.

• The dollar value of a one-tick move is calculated by multiplying the tick size by the size of the contract.

• The dollar value of a one-tick move in WTI is $0.01 x 1000 = $10

• Calculating profit and loss on a trade is done by multiplying the dollar value of a one-tick move by the number of ticks the futures contract has moved since you purchased the contract. 

• This calculation gives you profit or loss per contact, then you need to multiply this number by the number of contracts you own to get the total profit or loss for your position.

• A trader buys one WTI contract at $53.60.

• The price of WTI is now $54.

• The profit-per-contract for the trader is $54.00-53.60 = $0.40

• Therefore, the contract has moved $0.40 divided by $0.01 = 40 ticks

• The total move in dollars is 40 ticks x $10 per tick = $400

• The total profit would be $400 x the number of contracts the trader owns

Losses are calculated in the same manner as gains. 

Arbitrage

• Financial arbitrage is the simultaneous buying and selling of an asset in different markets to profit from a price difference.

• An arbitrageur exploits a market inefficiency by purchasing an asset at a lower price on one exchange and selling it at a higher price on another, locking in a low-risk profit. 

• Definitionally, arbitrage requires the borrowing of money (you have a zero-dollar cash outlay). However, colloquially, arbitrage tends to refer to taking advantage of a price difference to make a profit.

______________: Involves speculating on the outcome of a merger or acquisition. The arbitrageur buys the stock of the company being acquired and, in some cases, sells the stock of the acquiring company. The goal is to profit from the difference between the target company's market price and the acquiring company's cash offer.

Merger arbitrage

_________________: Exploiting a price discrepancy among three different currencies in the foreign exchange (forex) market. E.g., converting US dollars to Japanese yen, yen to euros, and then euros back to US dollars to profit from a temporary mispricing.

Triangular arbitrage

________________: Using complex quantitative models to identify temporary mispricings among statistically correlated assets. This method is more involved and relies on predictive models.

Statistical arbitrage

_________________: Involves exploiting pricing differences between a company's convertible bonds and its common stock. It typically involves buying the convertible bond while simultaneously short-selling the underlying stock. 

Convertible arbitrage

• Yes, there is an arbitrage opportunity.

  • Fair forward price: F = S*e^(rT) = $60*e^(0.05x1) = $63.08

  • Actual forward price: $65

  • The actual forward price is $1.92 overvalued than the fair forward price.

• Arbitrage strategy:

  • Sell the forward contract (agree to deliver stock for $65 in 1 year)

  • Buy the stock today at $60 by borrowing $60 at 5% interest.

  • At maturity in 1 year:

    • Deliver the stock and receive $65

    • Repay the loan for $63.08

    • Net profit is $65 - $63.08 = $1.92

• Yes, there is an arbitrage opportunity.

  • Fair forward price: F = S*e^(rT) = $60*e^(0.05x1) = $63.08

  • Actual forward price: $60

  • The actual forward price is $3.08 undervalued than the fair forward price.

• Arbitrage strategy:

  • Buy the forward contract (agree to buy stock for $60 in 1 year)

  • Short sell the stock today for $60 and invest the proceeds at the 5% risk-free rate

  • At maturity in 1 year:

    • Investment grows to $63.08

    • Buy stock via forward contract for $60 and return to borrower (cover short position)

    • Net profit is $63.08 - $60 = $3.08

• Yes, there is an arbitrage opportunity.

  • Fair forward price: F = S*e^((r+u)T) = $50*e^((0.05+0.02)x1) = $53.63

  • Quoted 1-year price is $60

  • The quoted price is $6.37 overvalued than the fair forward price.

• Arbitrage strategy:

  • Sell the futures contract for $60

  • Use the proceeds to buy oil at the spot price of $50 and then store for 1 year.

  • At maturity in 1 year:

    • Deliver the barrel of oil

    • Net profit is $60 - $53.63 = $6.37 per barrel

• Yes, there is an arbitrage opportunity.

  • Fair forward price: F = S*e^((r+u)T) = $50*e^((0.05+0.02)x1) = $53.63

  • Quoted 1-year price is $40

  • The quoted price is $13.63 undervalued than the fair forward price.

• Arbitrage strategy:

  • Buy the futures contract for $40

  • Sell oil inventory now (if you have it)

  • At maturity in 1 year:

    • Accept the delivery of the barrel of oil

    • Sell the barrel of oil in the spot market

    • Net profit is $53.63 - $14 = $13.63 per barrel

Contango

occurs when the futures price is higher than the spot price. This is considered a “normal” market condition because prices generally rise over time due to inflation. It is often seen as a healthy market.

• futures > spot → normal upward price expectation

Backwardation

occurs when the spot price is higher than the futures price. This can happen due to temporary supply-demand imbalances (for example, during COVID, oil prices went into backwardation because demand dropped).

• spot > futures → temporary market stress or supply shortage

contango vs. backwardation

Commodities often flip between contango and backwardation, depending on market conditions, but contango is generally expected in normal markets.

• Contango → futures > spot → normal upward price expectation

• Backwardation → spot > futures → temporary market stress or supply shortage