QCAA Physics Unit 3 & 4

The Problem of muon decay

The observation that even though muons only have a average life-span of 2.2 microseconds and the expected amount of muons to decay in a 1.91km journey, which would have taken 6.4 microseconds, would have been 527 out of the original 563, however in practice only 154 decayed.

Frame of reference

An arbitrary set of axes with reference to which the position or motion of something is described or physical laws are formulated

Relative motion

Motion where it is based off an observer's frame of reference. An object may be going at 10m/s to on observer stationary to earth, but only 5m/s to a observer riding their bike.

Theory of special relativity (short)

A theory that all motion must be defined relative to a frame of reference; Motion is completely dependent on the frame of reference the observer is in.

Inertial frame of reference

A non-accelerating frame of reference where Newton's laws of physics still hold.

The two postulates (assumptions) of the theory of special relativity

1. The Laws of physics are still the same in all inertial frames of reference.

2. That the speed of light in a vacuum, c, has the same value in all inertial frames of reference

Simultaneity

the relation between two events assumed to be happening at the same time in a frame of reference

Relativity of simultaneity

Two events that are simultaneous in one frame of reference are not necessarily simultaneous in another frame of reference

Proper time interval (t zero, t')

The time an observer at rest relative to an event; An observer on a moving bus is at rest to the bus.

Relativistic time interval (t)

The time an observer moving relative to and event; An observer sitting at a bus stop as a bus drives by is moving relative to the bus.

Time dilation

The difference in the time interval between then same event as measured by two observers moving relative to each other; The time interval changing as the observer at rest to the event experiences speeds near light speed.

The equation for time dilation

Where:

t' = proper time

t = relativistic time

v = velocity of object

c = speed of light (3*10^8 m/s)

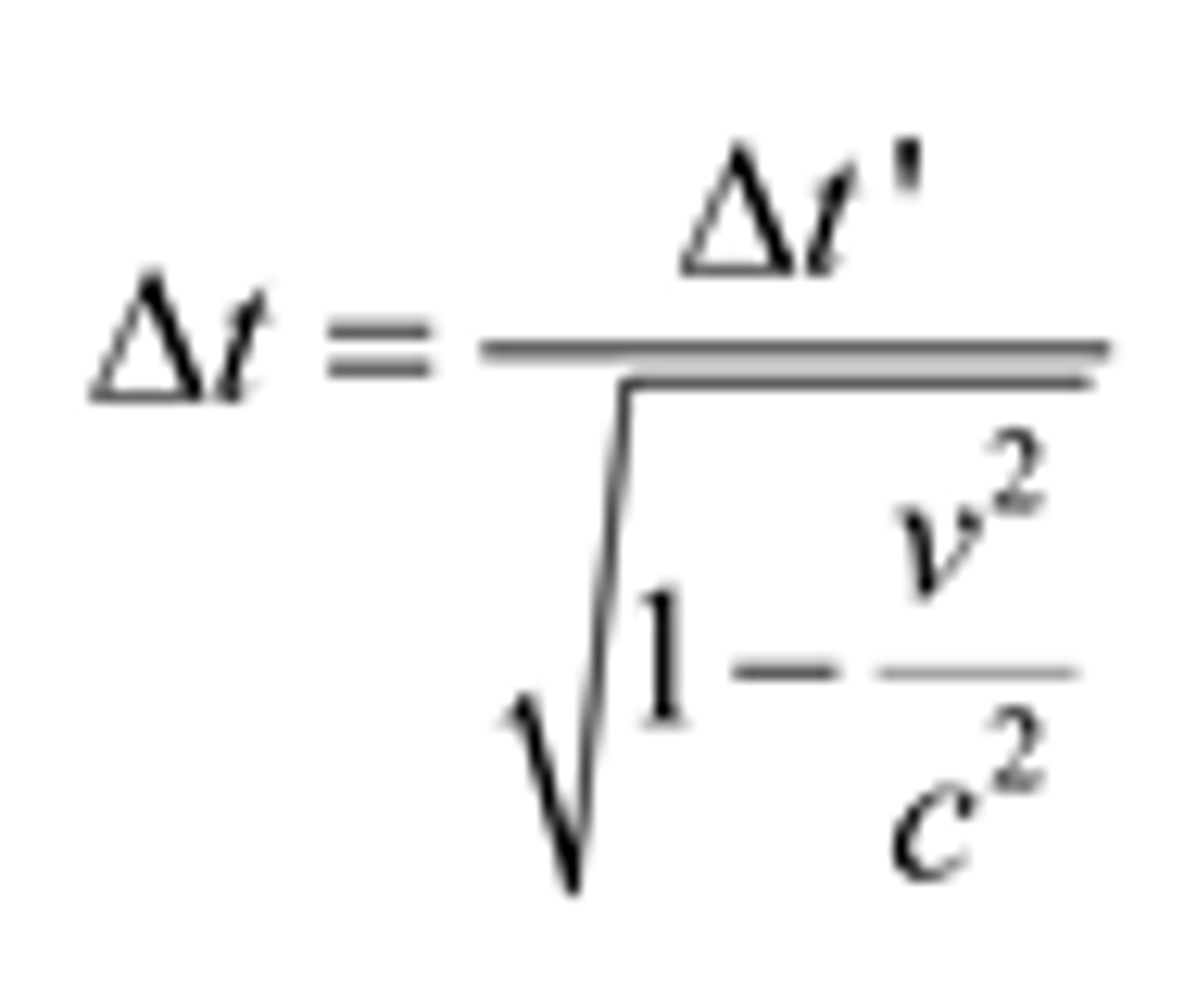
Proper length (L zero, L'

The length measured by an observer at rest relative to a event; An observer on a moving bus is at rest to the bus.

Relativistic length

The length measured by an observer moving relative to a event; An observer sitting at a bus stop as a bus drives by is moving relative to the bus.

Length contraction

The shorter length measured by an observer at rest to a object moving at near light speeds; The length measured by an observer relative to a moving object at near light speed shortening.

Length contraction equation

Where:

Lo = proper length

L = relativistic length

v = velocity

c = speed of light

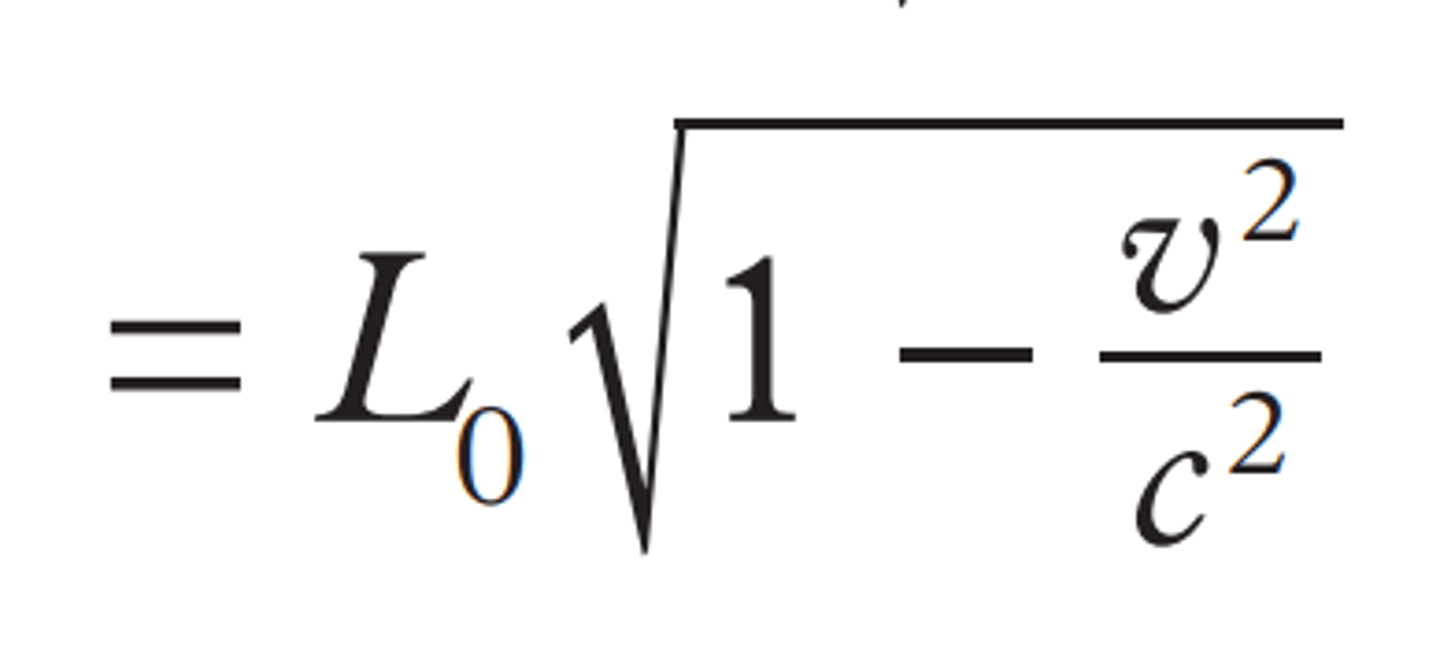
Light-year

A unit of distance, the distance traveled by light in a vacuum in one year (9.5*10^15m).

Rest mass

The mass of an object when measured in the same frame of reference as the observer.

Relativistic momentum

The momentum measured by an observer moving relative to an event; An observer sitting at a bus stop as a bus drives by is moving relative to the bus.

Conservation of momentum

A collision between two objects, will retain the same total momentum after the collision.

mass-energy equivalence

The conversion between mass and energy; E=mc^2.

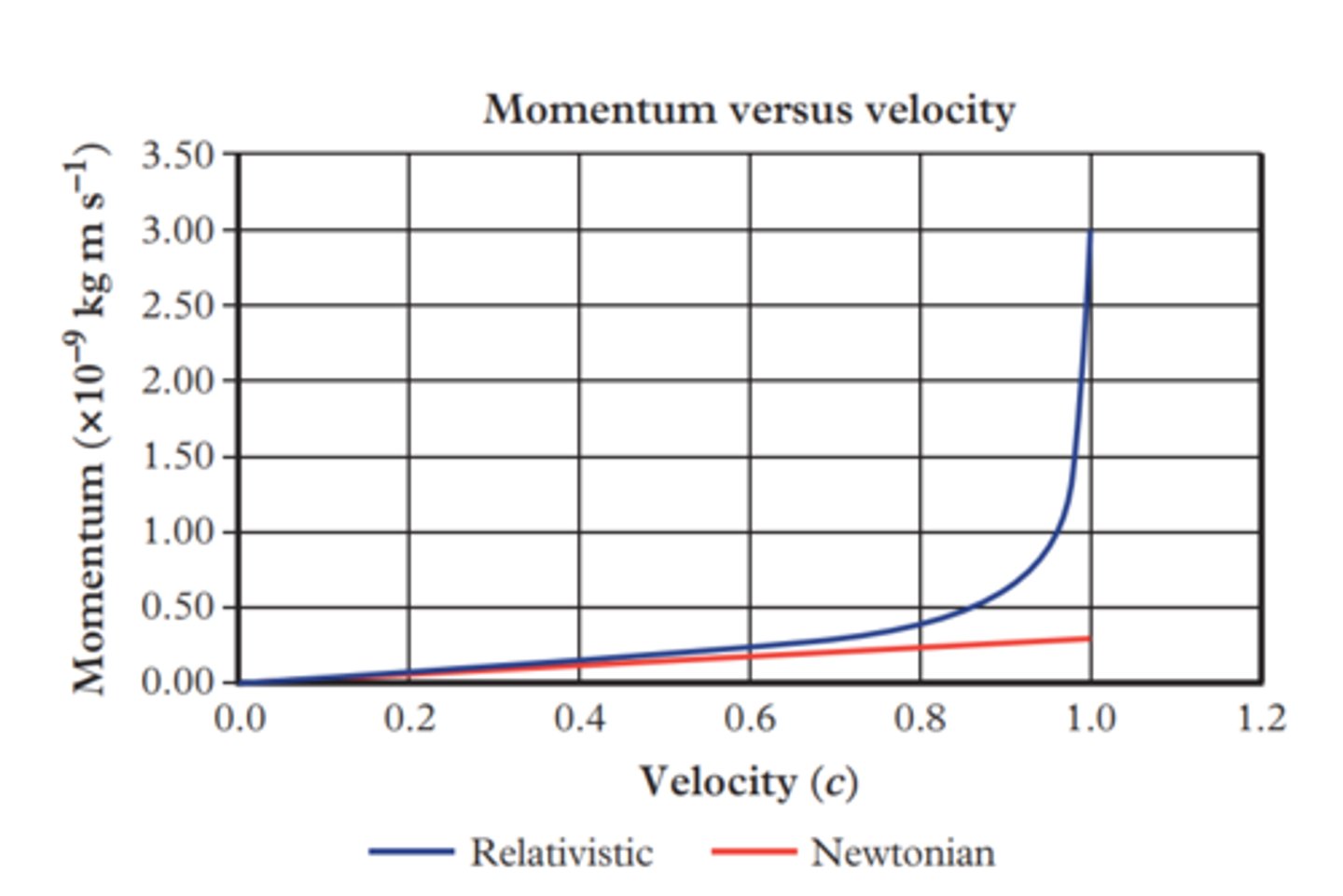
The reason why the speed of light cannot be exceeded or reached

As the graph shows, to increase a particles speed to light speed would require an infinite amount of momentum, as the speed of light is like an asymptote, unreachable.

Young's double slit experiment

One light source which shines through to identical slits side by side, into a dark box. The results of this show a series of light 'dots' inside the box. This phenomenon displays the constructive and destruction interference occurring as the light 'beams' collide. The presence of interference confirms that light does not only display properties of particles, but also wave like properties.

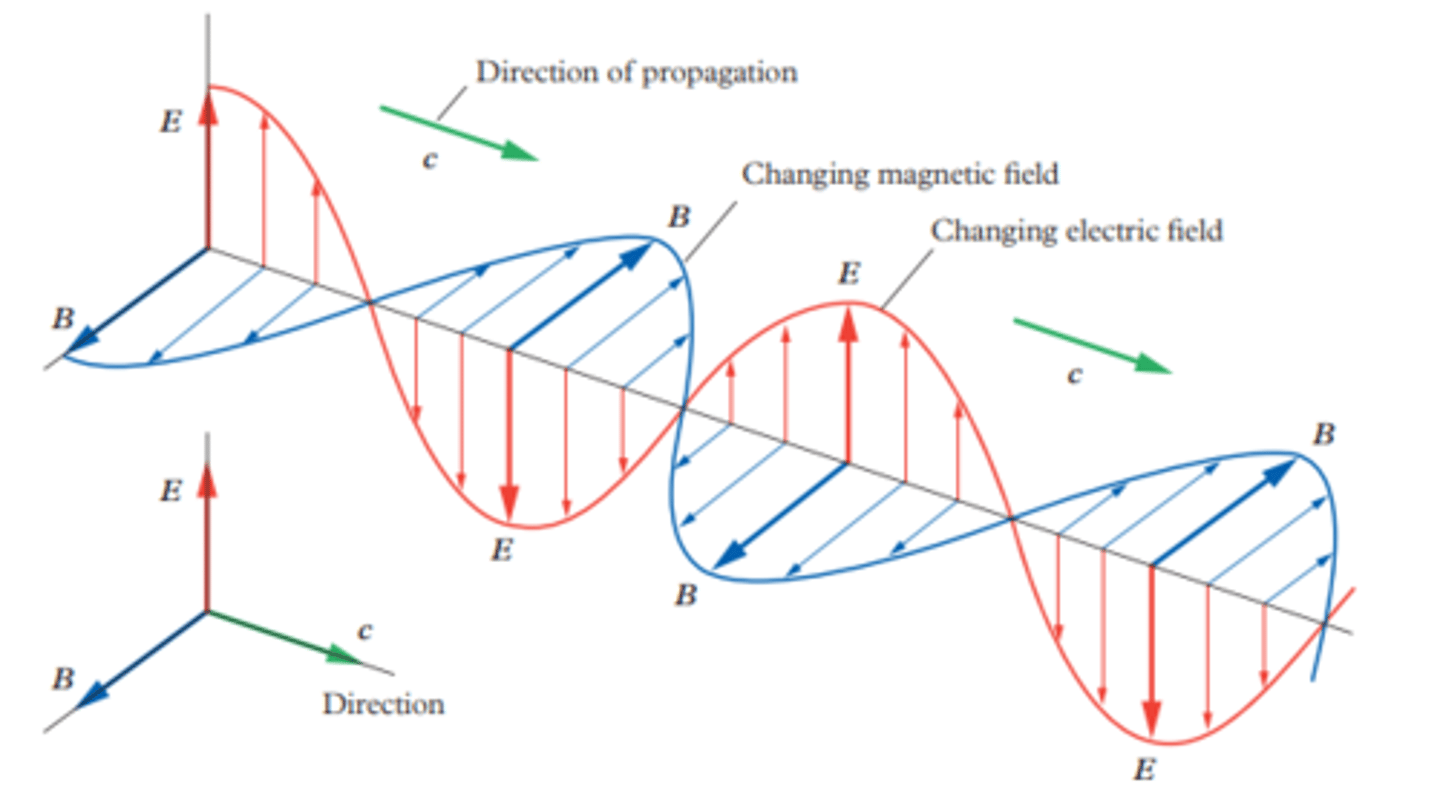
Electromagnetic wave

A wave produced by the oscillation of an electric charge, which radiates out at the speed of light as perpendicular electric and magnetic waves.

Magnetic field

A region of space in which a magnetic force is experienced. The field is produced from a moving electric charge.

Electric field

A region of space near an electrically charged object within within which a force would be exerted on other electrically charged particles or objects.

electromagnetic radiation

Energy radiating out as synchronized oscillations of electric and magnetic fields, or electromagnetic waves, propagated at the speed of light through a vacuum.

Wave model of light

Uses wave characteristics such as wavelength, amplitude and frequency to describe the behavior of light, such as polarization, interference and diffraction.

Limitations of the 'Wave model of light'

The wave model of light has difficulties explaining phenomena such as black body radiation and the photoelectric effect.

Black body

An object that absorbs all radiation falling onto it. It is a perfect a absorber or emitter of radiation.

Black body radiation

the radiation emitted by a perfect black body (a body that absorbs all the radiation that hits it).

Wien's displacement Law

States that the black-body radiation curve for different temperatures peaks a wavelength inversely proportional to the temperature; The higher the temperature of the black-body the lower the wavelength peak will be.

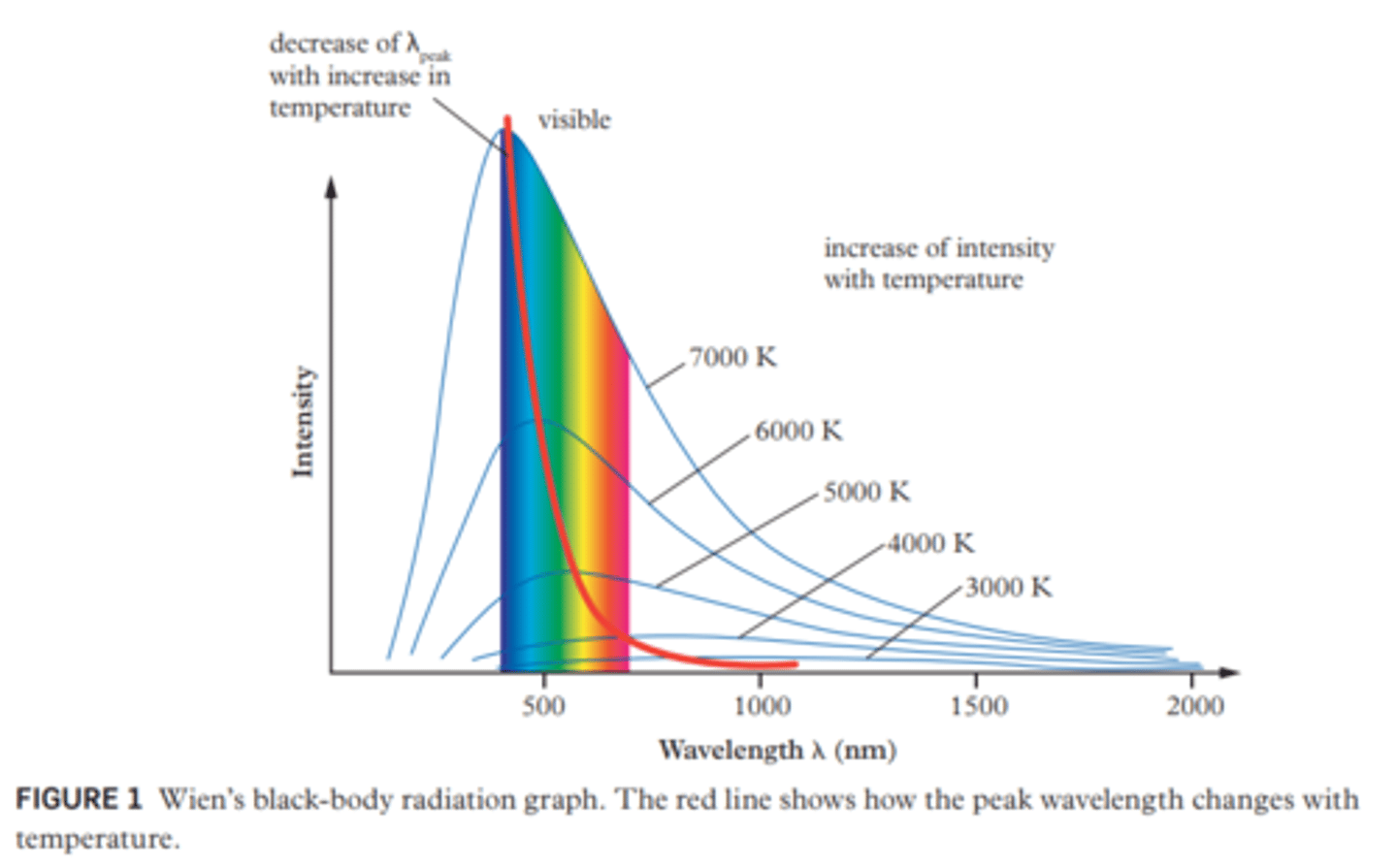
Quanta

The smallest discrete packets of energy of electromagnetic waves, later known as photons.

Discrete

individually separate and distinct.

Planck's constant

A constant used to relate frequency to energy 6.626 * 10^-34.

Planck's equation

Displays the relationship between frequency and energy. It accounts for the quantised nature of light and plays a key role in the understanding of phenomena such as the photoelectric effect and Planck's law of black-body radiation.

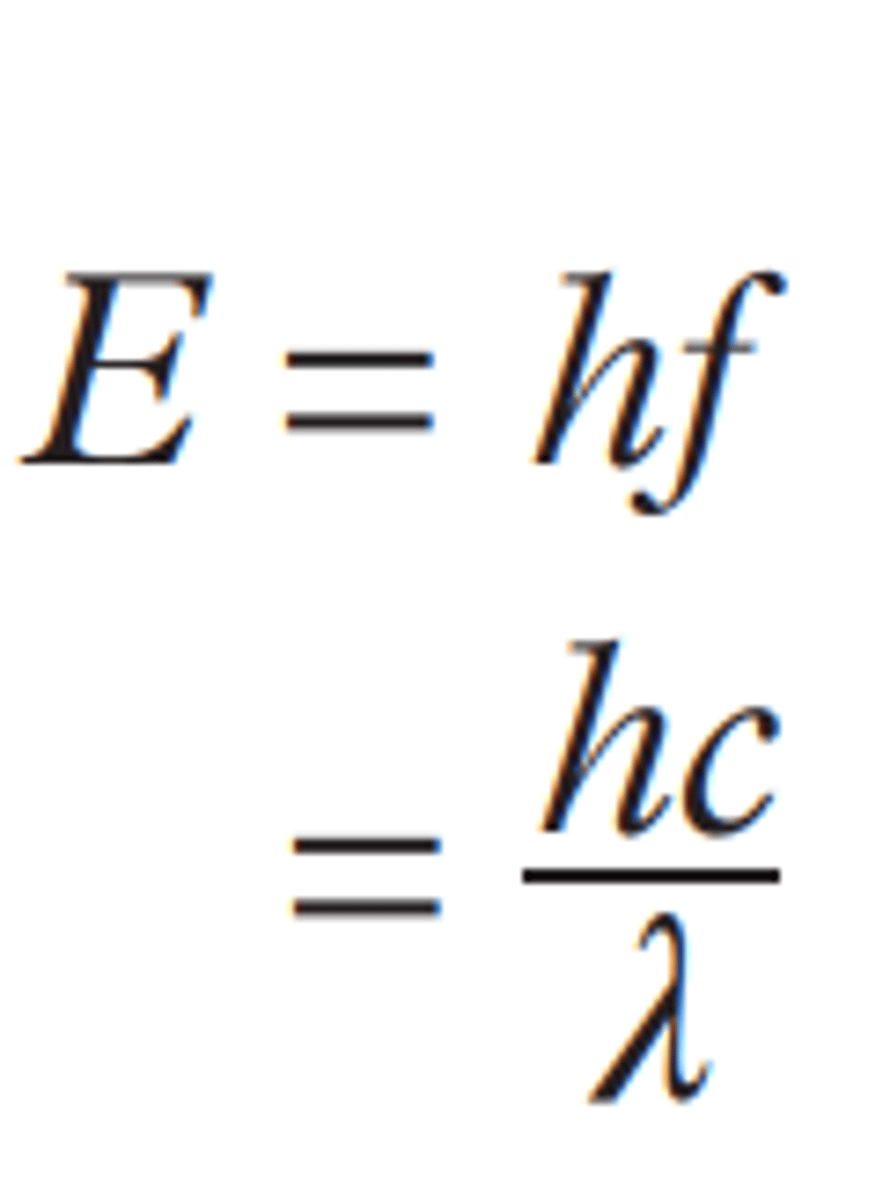
Quantised

Form into quanta.

Photoelectric effect

The emission of electrons (or other carriers) when light shines on a material.

Threshold frequency

The minimum required frequency of a photon that can eject a electron from a surface. It does not matter how intense the light source is, only that the frequency (energy according= to E=h*f) is higher then the threshold.

Photon

A quantum of all forms of electromagnetic radiation.

Stopping potential

The negative potential on the collector at which the photoelectric current becomes zero.

Work function

The minimum energy required to remove a election from a solid.

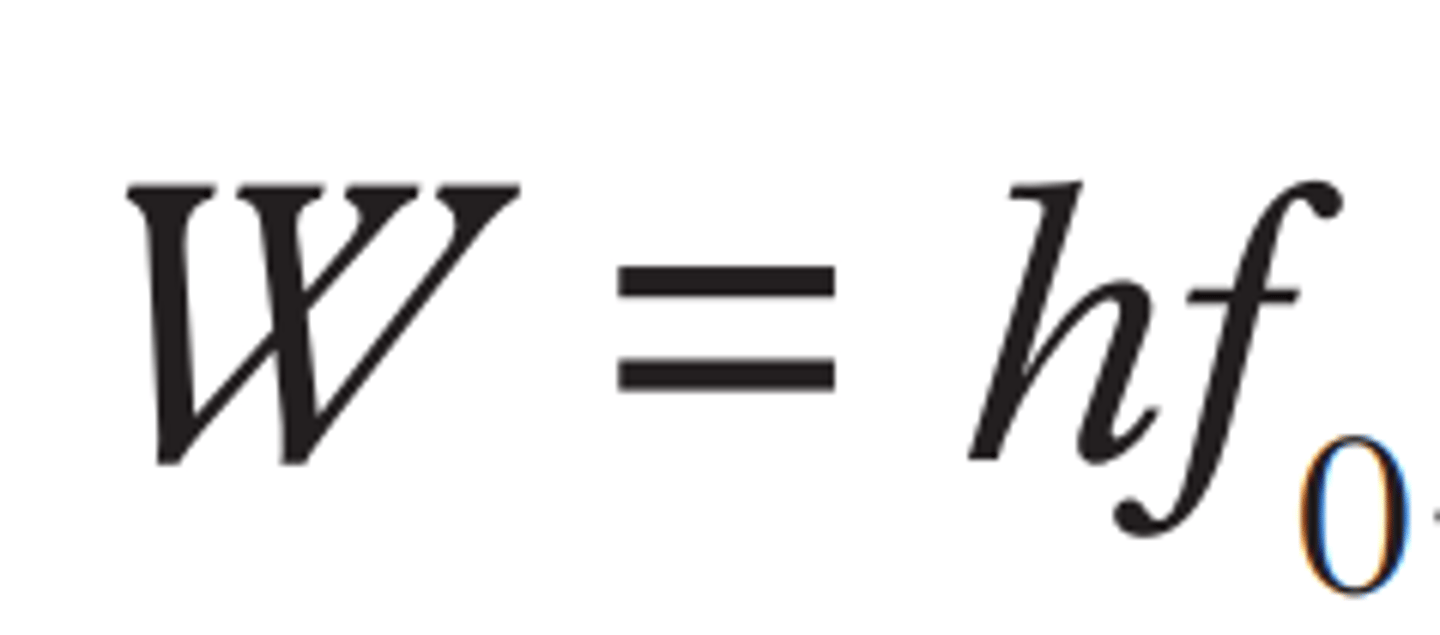
wave-particle duality

Every particle or quanta may be partly described as not only a particle but also a wave.

Rutherford's model of the atom

A small central positively charged nucleus, with negative electrons orbiting around it.

Limitations of Rutherford's model

1. Could not explain how electrons could experience centripetal acceleration, therefore continuously lose energy, and not collapse. Essentially the atom in this model should be unstable.

2. Could not explain the emission lines of the hydrogen spectrum; Cannot explain why certain wavelengths are absorbed, or are emitted in different spectrums.

Bohr's model of the atom

Electron orbit the nucleus in stationary states, with fixed angular momentum and energy,their distance from the nucleus being proportional to their energy. When an electron moves between stationary states, it is accompanied by the emission or absorption of a photon.

Stationary states

angular momentum

For circular motion, the momentum of a particle in which the velocity vector points along the radius of the circular path and is equal to mvr.

Bohr's postulates

1. Electrons in an atom exist in stationary states.

2. Transition between stationary states absorbs or emits electromagnetic radiation.

3. Angular momentum of a stationary electron is quantised.

Balmer's equation

Is used to calculate the wavelength required to make an electron jump a certain amount of orbitals.

Where:

RH = 1.097 * 10^7 1/m

nf = the final orbital the electron was in

ni = the intial orbital the electron was from

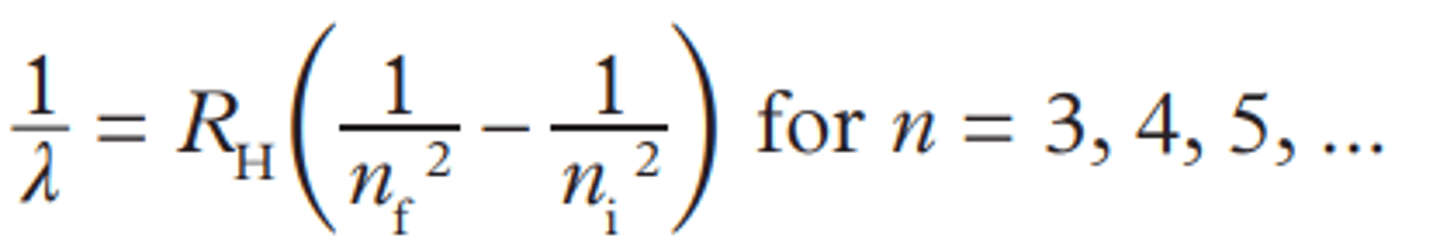
Limitations of Bohr's model of the atom

1. Spectra of large atoms

2. Relative spectra intensity

3. Hyperfine spectral lines

4. Zeeman effect

5. Stationary states

Note: Initially Bohr's model didn't really solve the instability of the atom due to centripetal force problem. This was solved later by de Broglie.

Electron probability cloud

A theory stating that instead of electrons actually orbiting the nucleus, they could just exist in a stationary position as but the position they are in is unknown, and their is no way of knowing. The only indication of position is the wave like 'cloud' of possible positions. This solved the problem of how an atom could be stable when the electron is under constant centripetal acceleration.

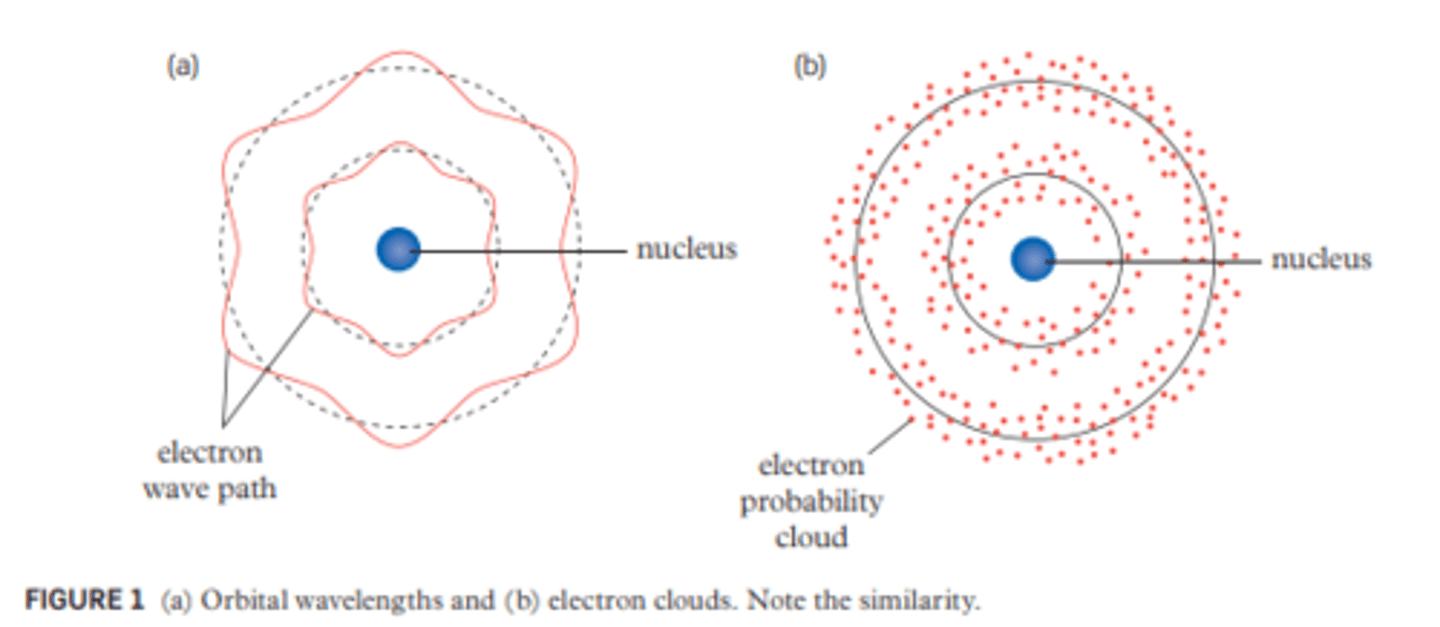
Wave-particle duality for matter

The discovery of the electron probability cloud, and its wave like manner, meant that matter could be similar to light, in that it can display wave and particle characteristics. This lead to the wave-particle duality for matter.

Standard model

A theory describing three of the four fundamental forces in the universe, as well as classifying all known elementary particles.

Elementary particle

A particle that with no substructure, and thus not composed of other particles.

Higgs boson

An elementary particle in the standard model that acts as a 'force carrier' for the Higgs fields - field that pervades the universe and is responsible for giving certain elementary particles mass. It is similar to the way a photon is a force carrier for the electromagnetic field

Particle zoo

A term used to describe the large variety of particles

Antiparticle of matter

A particle that has the same mass, but opposite charge and spin (dw about spin).

Antiproton

The antiparticle of the proton.

Has an electric charge of -1e.

Any collision with a proton causes both to be annihilated.

Antimatter

Matter composed of the anti particles that constitute ordinary matter

Quark

subatomic particles governed by the strong nuclear forces that constitute hadrons;

there are sic quarks in the standard model

Up +2/3e , Down -1/3e

Charm +2/3e, Strange -1/3e

Top +2/3e, Bottom -1/3e

Antiquark

Same mass as a quark but with opposite charge and spin (dw about spin).

Antiup -2/3e , Antidown +1/3e

Anticharm -2/3e, Antistrange +1/3e

Antitop -2/3e, Antibottom -+1/3e

Generation

A division of the elementary particles according to the Standard Model. There are three generations;

1st Top/Down,

2nd Charm/Strange,

3rd Top/Bottom.

Hadron

Particle composed of quarks and gluons

Gauge bosons

The four mediating particles that govern particle interaction. Their name and respective force they mediate are;

Photon - Electromagnetic force

Gluon - Strong nuclear forces

W&Z - Weak nuclear force

Baryon

A subatomic particle that is the combination of 3 quarks or 3 anti-quarks (if three anti-quarks it is a anti Baryon). Either has a charge of 1e, -1e, or 0e.

Meson

A subatomic particle comprised of 1 quark and one anti-quark. Are incredibly unstable, do do the quark and anti-quark destroying each other.

Leptons

A class of elementary particles, of which there are six of them. They do not form composite particles, that is, they are not building blocks (unlike quarks).

They have either one unit of electric charge or are neutral. The six types of leptons are;

Electron -1

Electron neutrino 0

Muon -1

Muon neutrino 0

Tau -1

Tau neutrino 0

All 6 leptons also have respective anti-leptons, where as standard, their charges are opposite.

Baryon number

A number describing the contents of a baryon. If the number is 1, it is comprised of quarks, if the number is -,1, it is comprised of anti-quarks, and if the number is 0 it is comprised of both (meson) or neither (lepton).

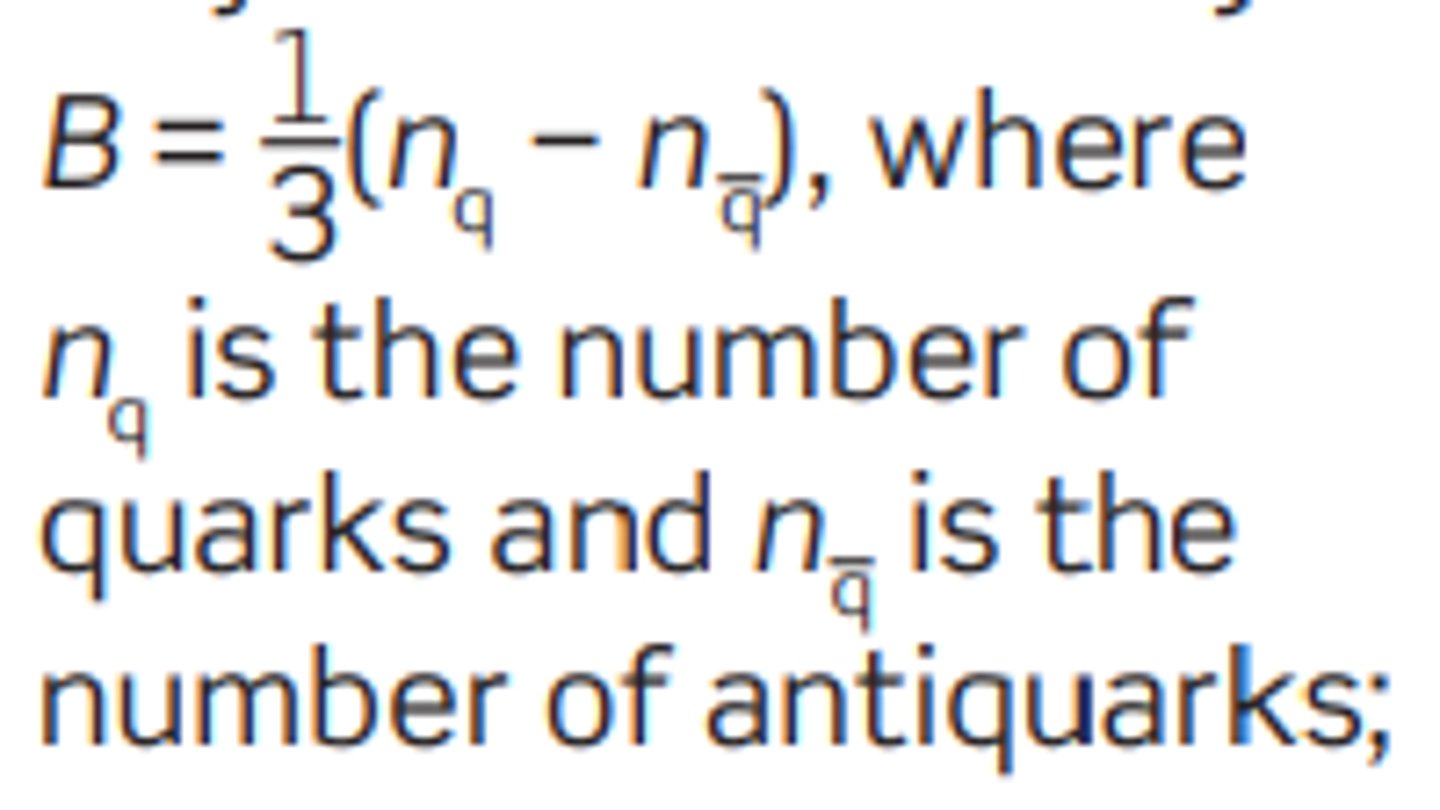
Lepton number

A number describing the nature of elementary particle reaction. The number represents the difference between the number of leptons and anti-leptons in a elementary particle reaction.

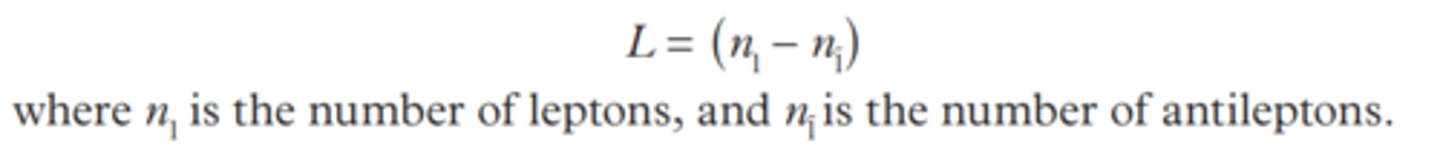
Conservation of Baryon and lepton number

That in any interaction the baryon and lepton number is conserved.

Feynman diagram

The graphical representation of particle interaction. With time along the horizontal axis and space long the vertical axis.

Representation of particle motion

Straight-line arrows in the direction of time, with the respective letter or character of the particle indicated.

Representation of antiparticle motion

Straight-line arrows in the opposite direction of time, with the respective letter or character of the particle indicated.

Representation of gauge bosons

Wiggly lines, with the respective letter or character of the type of boson indicated.

Vertex

The point where particles interact. At the vertex they will emit or absorb new particles, deflecting one another or changing type. Vertices are represented by a dot, or the point where the three lines meet.

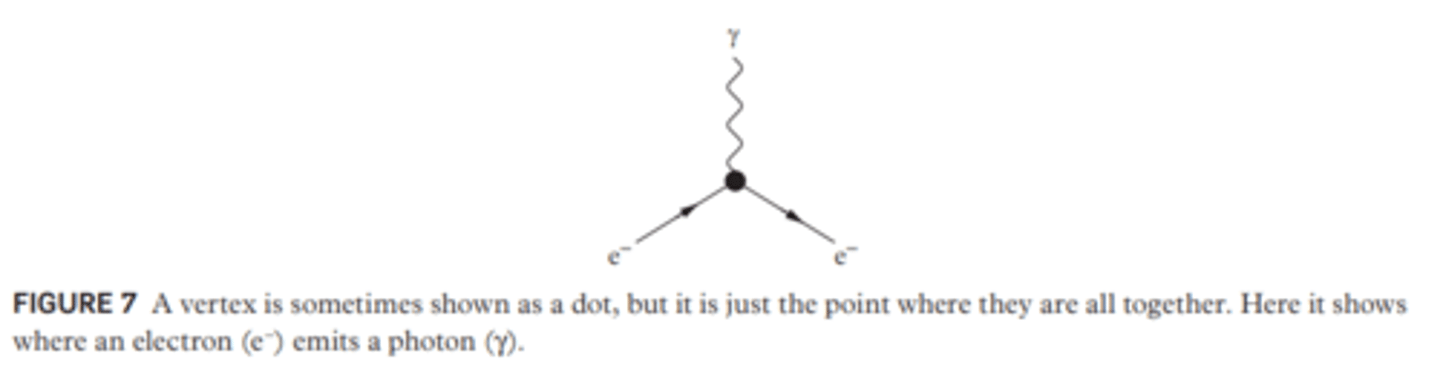
Vertex - location

For external particles (real particles) If the particle is incoming, the vertex will be to the right of the particle, if it is outgoing, the vertex will be to the left of the particle. For internal lines (representing virtual particles) the vertices are at both ends.

Electron - Electron interaction

As two electrons move closer (shown by the distance on the space axis decreasing between them) the electrostatic repulsion between the two negative charges gets stronger. This causes them to slow down as they near each other. Once close enough they exchange a photon, which repels each electron away from the other.

Electron - positron interaction

Symmetry

When a particle interaction is subjected to to a certain operation and it appears exactly the same after the operation.

Charge-reversal symmetry

Interactions that are not affected if all charges are swapped

Time-reversal symmetry

And interaction that looks the same if the flow of time is reversed (products become reactants, reactions become products).

When solving problems involving gravity and motion, how do you know whether gravity should be positive or negative?

If the object is going against gravity (upwards) then it will be negative. If the object is going with gravity (downwards) then it will be positive.

when analysing a graph, what do you say about it?

Describe the trend (e.g "positive linear trend" or "quadratic relationship/ indirectly proportional") and justify it with the r-squared value.

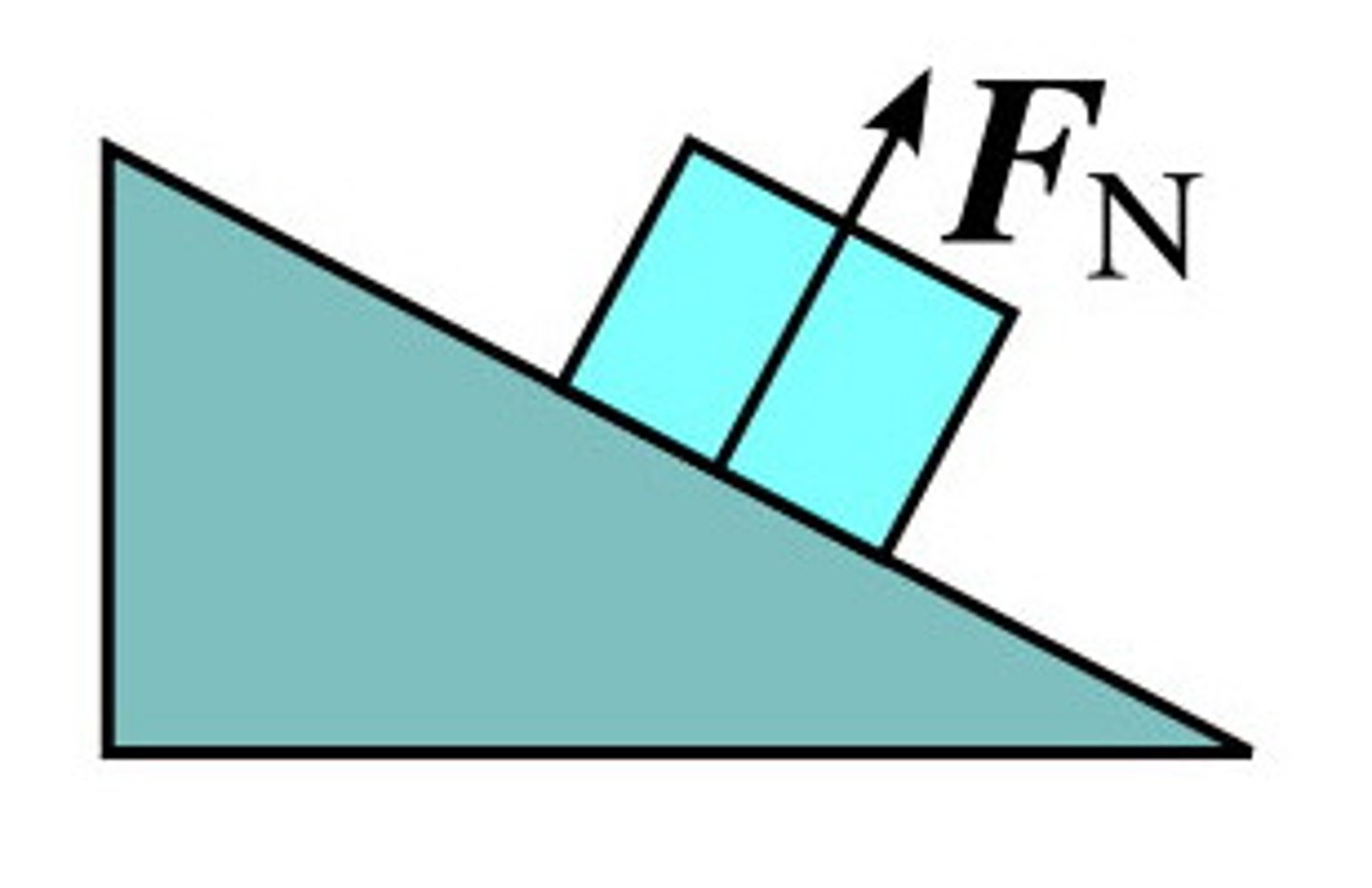
Define the normal force

A force acting perpendicular to the surface.

How do you calculate the force of gravity on an object?

F = mg

What is Newton's first law?

An object stays at rest unless acted on by another force (This is called inertia).

What is Newton's second law?

F=ma

What is Newton's third law?

Every action has an equal and opposite reaction.

What is friction?

A force that opposes motion

What is the net force?

The sum of all forces acting on an object

What does it mean when the net force equals zero?

There is no acceleration. The object is either not moving or travelling at a constant velocity.

What is tension?

The force exerted by a rope, cable, chain, etc.

If an object is being hoisted upwards, with an acceleration by a chain, how do you calculate the tension in the chain?

Fₜ = Fₙₑₜ + Fw

where Fₙₑₜ = ma (acceleration of the object moving upwards)

What is a force applied at an angle?

An object on a FLAT surface being pulled by a rope/cable/chain at an angle.

How do you calculate the normal force when there is a force applied at an angle?

The vertical force exerted by the rope/cable/chain decreases the normal force.

So, Fₙ = Fw - Fᵥ

When an object is on an incline, how do you calculate the applied force or force going downwards?

Fₐ = mgsinθ -Ff (if friction is present) down incline

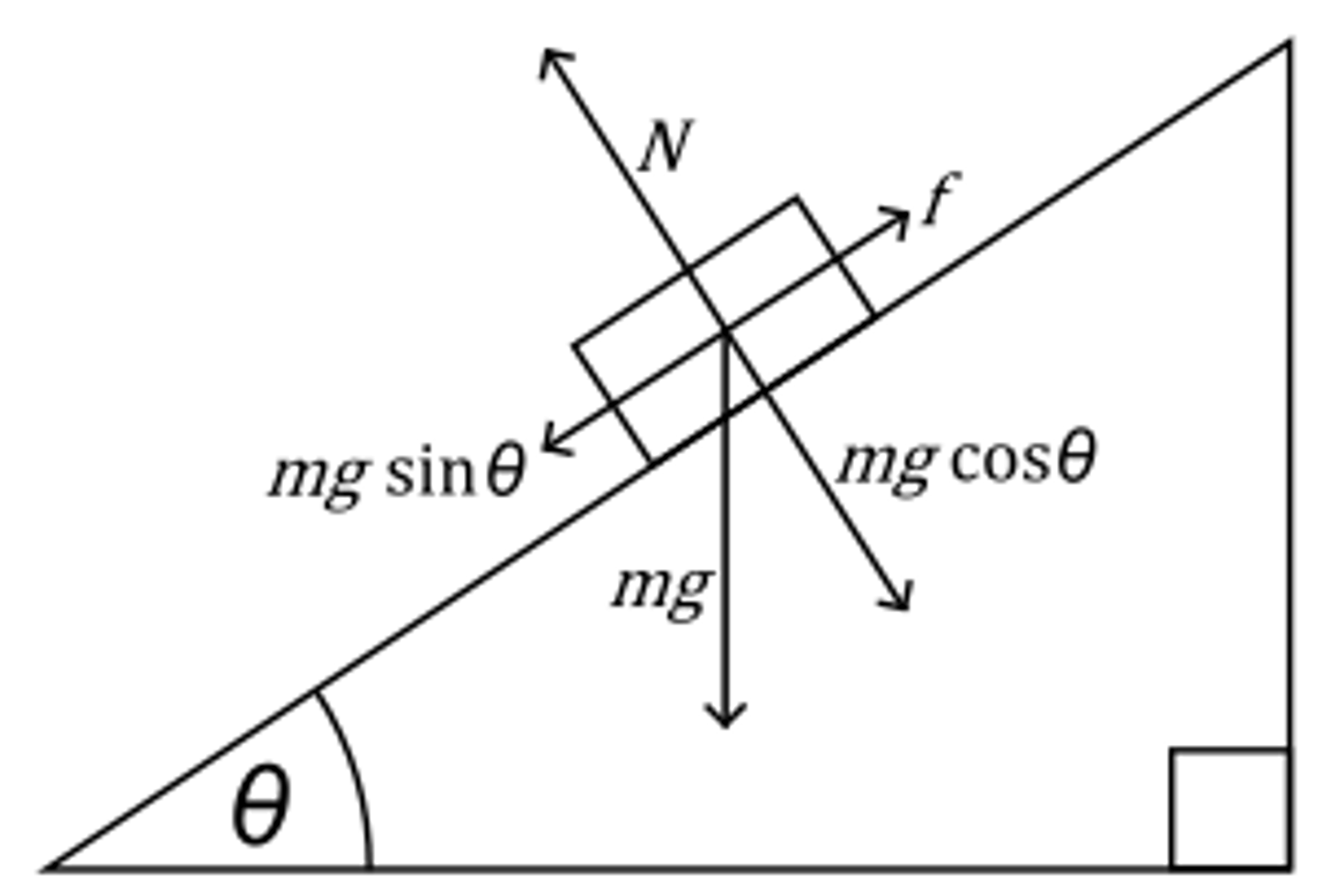
How do you calculate the force of friction?

Ff = mgsinθ - Fₐ

OR

Ff = µ Fₙ

where µ is the coefficient of friction.

How do you calculate the normal force of an object on an inclined plane?

Fₙ = mgcosθ perpendicular to incline

How do you calculate the tension in a rope pulling an object up an incline at a constant speed?

Since the objects is travelling at a constant speed, a=0. Therefore, Fₙₑₜ = 0

So, Fₜ = mgsinθ