AP Calc Unit 1

a straight line [vertical] =

undefined

what conditions make a limit discontinous

jump discontunity

removable

asymptotes

Determining a chart from the left and right side of limit

Ensure the numbers are very close to each other 

if not

find the slope as it reaches the limit to find the # as it reaches a certain x

Chart slope example

jump discontinuity

the function starts somewhere else completey

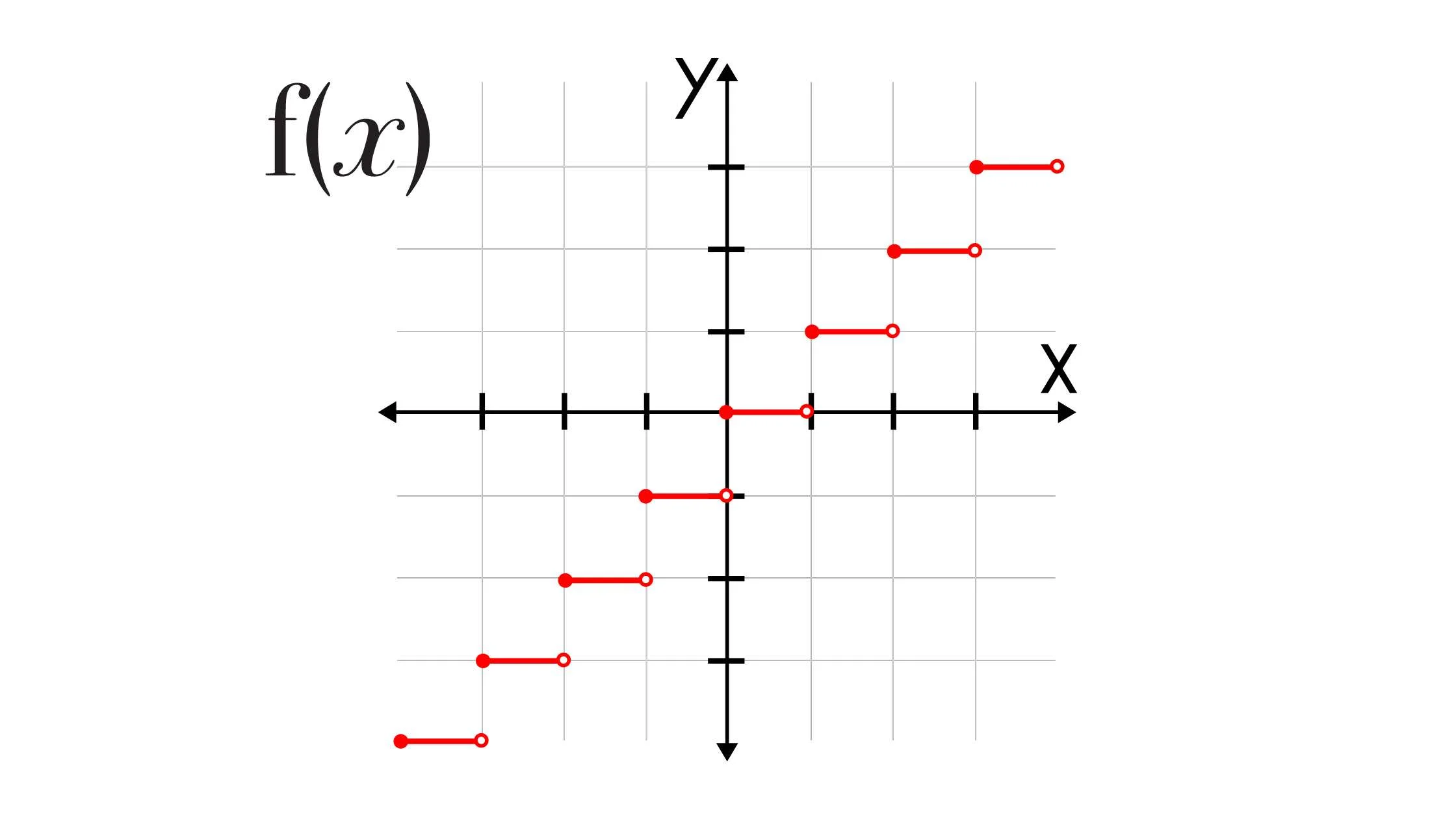
Removable discontinuity

the function is all in one except for one point

Constant Multiple

Lim(3 x f(x)) =

3 x (Lim f(x))

Sum

Lim (f(x) + g(x)) =

Lim f(x) + Lim g(x)

Difference

Lim (f(x) - g(x)) =

Lim f(x) - Lim g(x)

Product

Lim (f(x) x g(x)) =

Lim f(x) x Lim g(x)

Quotient

Lim (f(x)/g(x)) =

Lim f(x) / Lim g(x)

Power

Lim (f(x))ⁿ =

(Lim f(x))ⁿ

Root

Lim square root f(x) =

square root all of Lim f(x)

Trig mem

Sin [π/3] → 30 degree

[√3]/2

Trig mem

Sin [π/4]

[√2]/2

Trig mem

Sin [π/6] → 60 degree

1/2

Trig mem

Cos[π/3]

1/2

Trig mem

cos [π/4]

[√2]/2

Trig mem

cos [π/6]

[√3]/2

Trig mem

Tan [π/6]

[√3]/3

Trig mem

Tan [π/3]

√3

Trig mem

Tan [π/4]

1

sin x =

cos [90 -x]

aka the compliment

Trig mem

sin [π]

0

Trig mem

cos [π]

-1

Trig mem

tan [π]

sin [π] / cos [π]

Trig mem

Tan [π/2]

sin [π/2] / cos [π/2] = 0

Trig mem

sin [π/2]

1

Trig mem

cos [π/2]

0

Trig mem

sin [3π/2]

-1

Trig mem

cos [3π/2]

0

Trig mem

tan [3π/2]

0

Think of cos as

X coordinate

Think of sin as

Y coordinate

Trig mem

cot 

cos / sin 

or x/y

or 1 / tan

When do you use trig function theorems

1. when x is approaching zero

2. when the answer from substitution is originally #/0

an absolute function

found in a piecewise 

Expand the condition 

1. determine the number of x by solving for it [use only the eq. in the absolute bracket]

2. the first eq is the original eq in brackets when x > #

3. the 2nd is negative times the eq when x< #

An absolute functions limit

→ 0/0 version

plug in the limit from the closest number from the left or right side

2⁺= 2.1

2^- = 1.99

Squeeze theorem

determining the limit of a function if it equals two others

g(x) < f(x) < h(x)

A fraction equals #/0

a infinite limit

A fraction equals 0/0

you will use a form of cancelling out

“estimate of instantaneous rate of change”

determine the slope using two points

a horizontal slope

equals zero

IVT Purpose

to determine continuity on an interval

when x=3 it is undefined

still can be continuous 

piecewise function

a # told to be solved for isnt in the function

it is immediately cont. at that point

An absolute functions limit

→ #/0 version

Solve for a ± infinity

is to be treated like a regular absolute → all outcomes positive

Log (1)

0

square root of one also equals

one

a³- b³

[a - b] [a²+ab+b²]

a³+ b³

[a +b] [a²- ab +b²]

limit of cancellation of outter and inner fraction

1. make the denominators of both the same

2. do the outter inner rule

3. leave any multiplication undone → e.g 3x[x² +2]

4. any opposite subtractions leave out an -1 in their place → e.g. 3-x = [-1][x-3]

Limits of conjugate 

1. square the num or den of the square root 

2. the new eq is the same except, everything but the root gets squared 

3. The opposite side of the fraction is multiplied by the square root eq except swap the ± for the opposite 

piecewise function

reading 2^- and 2⁺

1: less than 2

2: greater than 2 

→ if x doesnt equal 2 then both fall into that category

a trig function equals 0/0 or approaches 0

apply special rules 

Trig special theorem

sin x/ x

1

Trig special theorem

sin ax/ bx

or 

ax/ sin bx 

a/b

Trig special theorem

sin² ax/ bx²

a²/ b

Trig special theorem

a sin bx/ cx

[a x b]/ c

Trig special theorem

x / sin x

1

Trig special theorem

tan x/ x

1

Trig special theorem

tan ax/ bx

or

tan ax/ tan bx

a/b

Trig special theorem

all the cos functions that equal zero

1. cos x -1/ x

2. cos ax -1/ bx

3. cos x but as it approaches π/2

4. 1 - cosx/ x

5. 1 - cos ax/ bx

large trig theorem functions 

split into two sections where u recognize where the top and bottom match

a function is always cont. if it is a

exponential or quadratic function

determining continuity

1. x = # must exist in domain

2. limit of x must exist

3. f(#) must equal existing limit

recognizing discontinuity

piecewise: not in domain

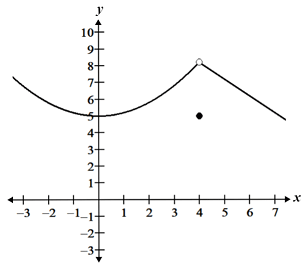
a removeable discontinuity

recognizing discontinuity

piecewise: Limit DNE

a jump discontinuity

determines variables that allow f(x) to be continuous on all real #’s

1. Determine all X’s

2. find eq that determines limit of all x’s

3. substitute the x in

4. distribute and turn into a system of equations

5. solve for both variables

if functions f and g are continuous at a

then subtracting, adding, dividing, or multiplying and g of a are all continuous

Infinite limits

a fraction as x approaches zero or equals #/0

plug in x as “a little more/less than x”

determine positive or negative num and den then apply the answer as ± infinity

Finding the vertical asymptote

set the den equal to zero 

if needed factor the den

cancel if possible 

As x → infinity

of a polynomial

If even is the highest power

1. x approaches + infinity = + infinity

2. x approaches - infinity = + infinity

---

If odd is the highest power

1. x approaches + infinity = - infinity

2. x approaches - infinity = + infinity

As x → infinity

#/ xⁿ

As you plug in infinity as x = youre left w the answer 0

As x → infinity

Function of fraction rules

REFERING TO POWER OF X

N > D = a/b → divide w/ x→ then plug in infinity w ±

N = D = a/b

N < D = 0

infinity/ #

± infinity

As x → infinity

When there is a perfect square root 

if the power is even sub x as |x|

if the power is odd sub x as x

As x → infinity

When there is a perfect square root: |x| edition

if x → - infinity:

sub as a negative x

As x → infinity

e^x

approaches + infinity = + infinity

approaches - infinity = 0

if 1/e^+infinity = 0

Horizontal asymptote

use the power rule of infinity

if N > D = no H.A.

IVT

“show that the eq has a solution on interval [#,#]

x is zero and one for example

sub both and determine in # asked for falls within the interval

→ in this case zero bc “solution” was asked for

IVT 

explain 

x exists on the interval due to IVT

→ note if asked could c exist on the interval = no bc ivt is must be there not could

Regular trig functions

simplify to the most before plugging in x