Lecture 6: Constrained Consumer Choice

What is the optimal choice?

It maximizes the satisfaction a consumer can achieve given a limited budget

Utility maximization occurs under the ____________

budget constraint

What is the optimal choice on the graph?

It lays on the budget constraint(affordable) and on the highest indifference curve(maximizes utility)

For Cobb-Douglass what would be the constrained choice?

The bundle on the budget line, the bundle on the highest indifference curve

If the point lands above the budget line?

Not feasible

If the point lands below the budget line?

Leave money

What does the optimal choice graph look like?

MRS= -MU1/MU2 = MRT = -P1/P2

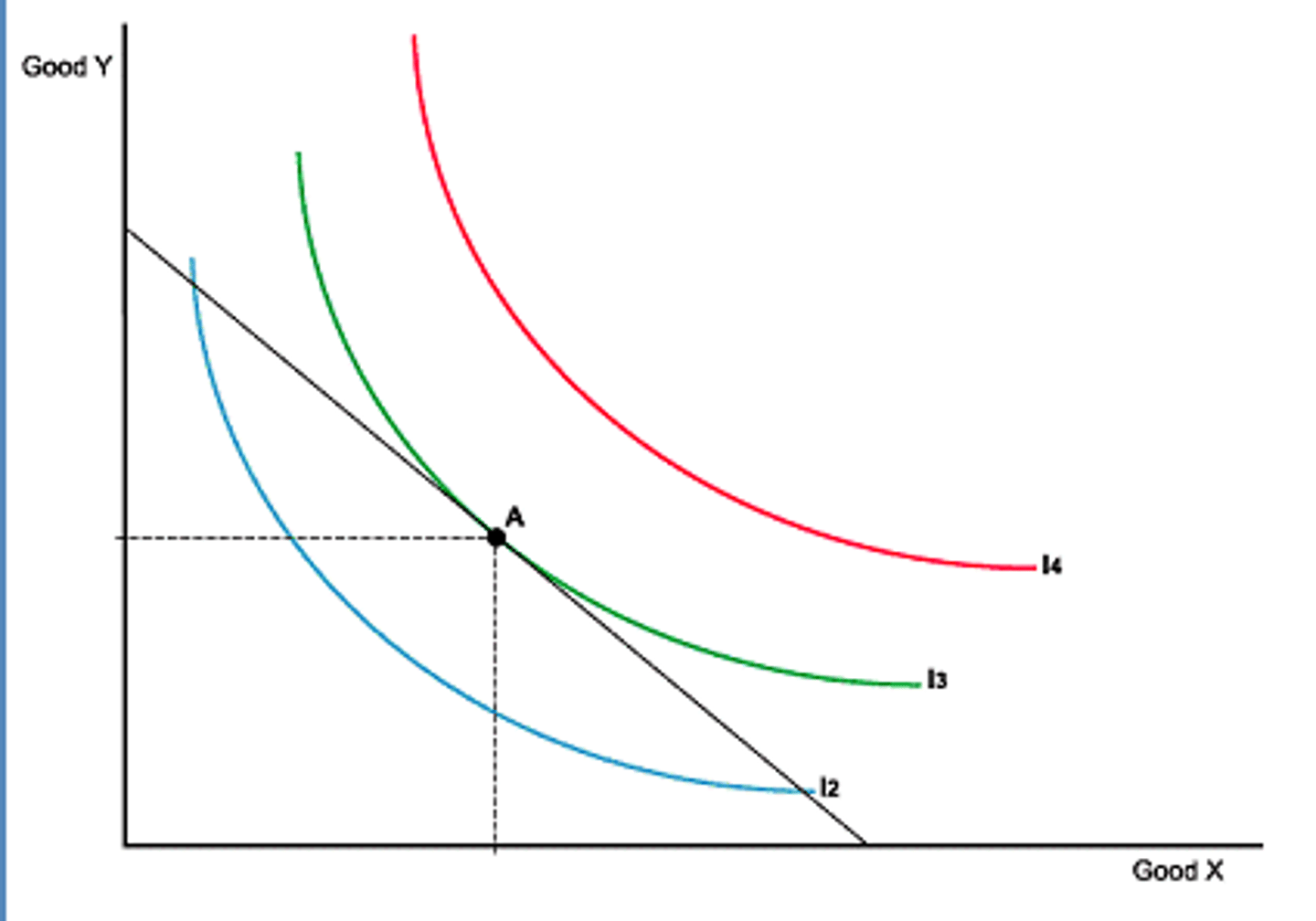
What is the condition for optimal choice with convex preferences? (Hint it's an equation)

MRS= -MU1/MU2 = MRT = -P1/P2 (MRS=MRT)

For non-convex preferences the tangency in the indifference curve and budget constraint will lay on the _________. Draw the graph.

horizontal and vertical axes

What does the graph look for perfect complements in constrained choice?

Answer

What is the utility function for perfect complements?

U(X1,X2)=min(X1,X2)

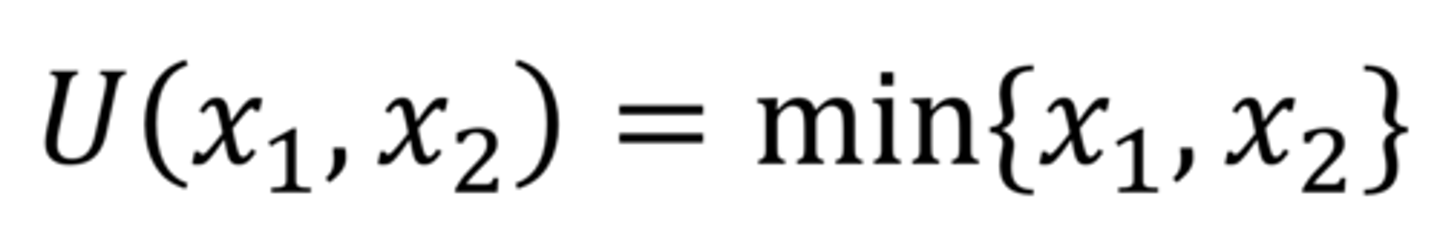
Practice Problem: U= (X1,2X2) Income= 12, P1=P2=1. What is the most optimal bundle?

2x2+x2 = 12 -> 4, 2(x2)->8

If U = X1 + X2 if P1 < P2 then which x would you purchase?

Only purchase X1, X2 = 0

If the budget constrant is 100 = 1X1 + 2X2 which x would consumer buy?

X1 becuase it's cheaper

If P1> P2 and the budget constraint is 100=2x1 + 1x2 then...

x1 is more expensive than x2 and onyl buy x2

If P1= P2= 1? U = X1 + X2, P1 = P2 = I I = 4 then what is the optimal bundle constraint?

Anything on the budget line