chem20212 - electrochemistry

electrochemistry, quantum, electronic structure

equation for molarity

c = mol dm-3

V = dm3

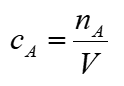
molality equation

m = mol kg-1 M = molar mass kg mol-1

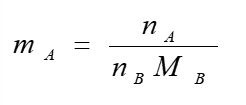
mol fraction equation

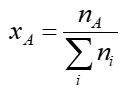
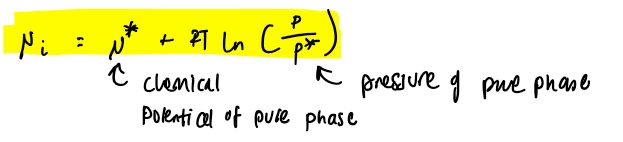
chemical potential equation of an ideal gas in pure phase

μ = J mol-1 G = J

• chemical potential is the molar gibbs of the pure phase at constant p,T if it behaves ideally

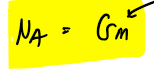
chemical potential and gibbs free energy at equilibrium

• ΔG = 0 at equilibrium therefore chemical potential is constant

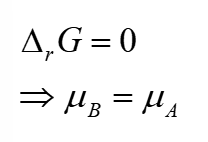
chemical potential of a real gas - expansion at constant T

μ = J mol-1 p = Pa = J m-3

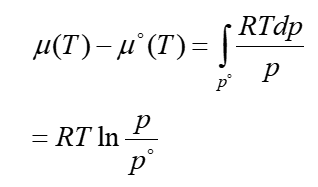
total gibbs energy before mixing ideal gases

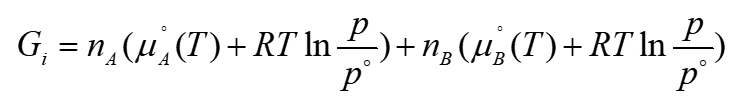
total gibbs energy after mixing ideal gases

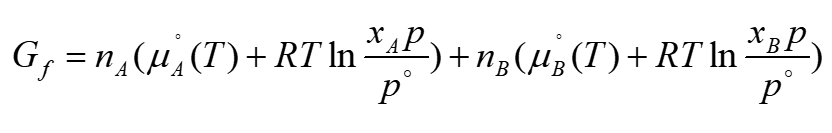
total Gibbs energy of mixing ideal gases eq. how does this prove spontaneity

• shows that mixing ideal gases is always spontaneous because ΔG = -ve

• xi < 1 and nRT = +ve → -ve + +ve = -ve

Gibbs energy of mixing ideal gases at not equal pressure eq

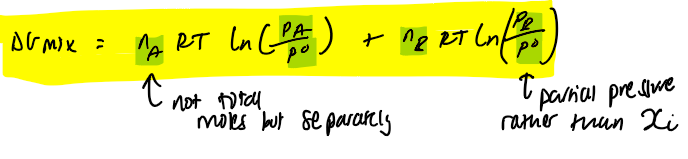
total entropy of mixing

• the bottom part is the derivation

free gibbs energy equation

chemical potential of real gases

φ = fugacity → its an effective pressure, correcting for non ideality

• deviation between chemical potential of ideal gases and real gases is due to attractive Van Der Waal interactions

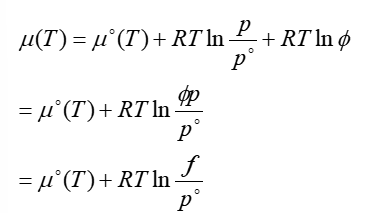
chemical potential of ideal solutions

raoults law eq and argument

• argued that mol fraction in solution reduces vapour pressure of certain mixtures from the pressure in pure phase. shown in eq

• he takes the assumption that components in solution will behave like ideal gases → mixing of gases is driven by entropy so ΔH mix = 0 → no change in interactions before and after mixing

• this will only be approximately accurate if A is surrounded by A ( A being solvent)

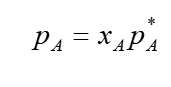
chemical potential of solution according to Raoult’s law

• assumption is made that components in solutions behave like real ideal gases

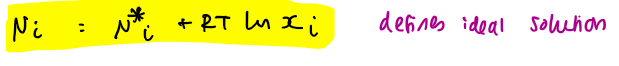
Henrys law

K = empirical constant for pure component B

• about ideal dilute solution

• implies interactions before / after mixing are different → will be approximately valid when B is surrounded by other molecules (A) . B being the solute

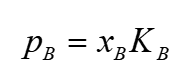
what does it mean by colligative properties

• important properties of liquid solution → Tm, Tf, b.p elevation

• this is dependent on the amount of solute not its identity

what are the two arguments for why chemical potential in pure phase > actual chemical potential

1. thermodynamic origin of solution stability

   • solution formation ΔG = -ve

   • in pure liquid ΔS is increased by evaporation → more favourable to be in evaporated state

   • in solution the motion is more random (ΔS is higher than in pure phase) → lower thermodynamic tendency to evaporate

2. semi quantitative argument

   • chemical potential eq for ideal solution is μA = μA* + RTlnχA

   • we know μA < μA* because the latter part of the eq is -ve

   • we know at equilibrium μA(l) = μA*(g)

   • if μA is lower in solution, we need higher temp to make it boil and lower temp to make it freeze

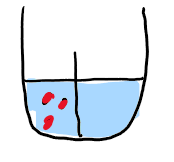
what happens to this over time

• diluting the solute is favourable, therefore pressure increases in solution compartment

• called osmotic pressure

• driven by thermodynamics

osmotic pressure equation for dilute solution (when xB v. small)

Vm = molar volume

• apply this to water purification

• if p > Π then water will be squeezed out

change in boiling temperature eq

• can switch xB with mB because xB < < 1

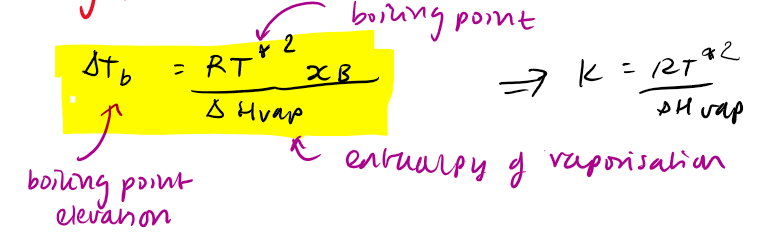
change in freezing temperature eq

• can switch xB with mB because xB < < 1

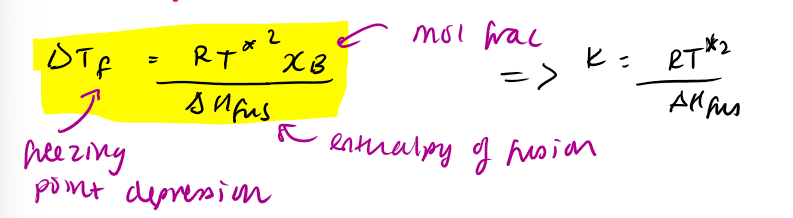
why are alcohols / water and electrolytes not ideal

• ideality means interactions before = after mixing

• alcohols and water have H bonding when mixed

• electrolytes conduct electricity when dissolved → display strong water - ion interactions

compare strong and weak electrolytes

1. strong - completely dissociate → degree of dissociation is independent of concentration

2. weak - partially dissociate → degree of dissociation is a function of concentration

what is the definition of the gibbs energy of solvating an ion

• the energy required for 1 mol of gaseous ion to become 1 mol of solvated ion

• its difficult to measure solvation parameters for individual ions → because other interactions occur

Borns approach to ion solvation - gibbs energy in vacuum

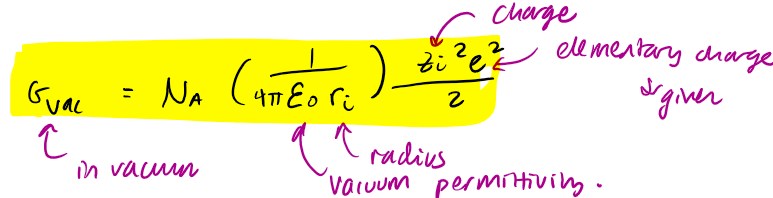
Borns approach t o ion solvation - gibbs energy of solvent

Born’s approach to ion solvation - Gibbs energy of solvation

• meaning it’ll always be favourable for ions to solvate

• as the εr increases ΔG solvation will become increasingly -ve

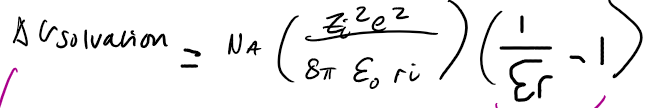
how does transport in electrolytes work

• you can force ions to move in a certain direction if you apply a potential difference between two electrodes

• this produces an electric field

• charge carriers migrate to the oppositely charged electrode → cations to cathode , anions to anode

ohms law

V = voltage

I = current (A)

R = resistance ( Ω ≡ V A⁻¹

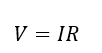
conductance eq

G = conductance

R = resistance (Ω)

k = conductivity (Ω⁻¹ m⁻¹)

A = area (m²)

l = length (m)

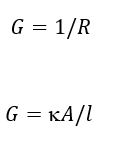
conversion from ohm to siemens

conductance definition

how easily the current will flow through a material

conductivity definition

• intrinsic ability of a material to conduct electricity

• it increases with concentration increasing. but as conc increases the conductivity will increase by a smaller amount

molar conductivity eq

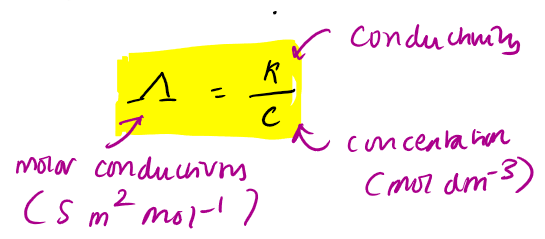
Kohlrauch eq for molar conductivity

• molar conductivity decreases as conc increases because interactions with ions. the more interactions the less it can conduct as they are slowed down

limiting molar conductivity eq

Λ⁰ = limiting molar conductivity, i.e. at infinite dilution (m² Ω⁻¹ mol⁻¹)

ν = stoichiometric factor

λ = molar conductivity of ionic equivalents (m² Ω⁻¹ mol⁻¹)

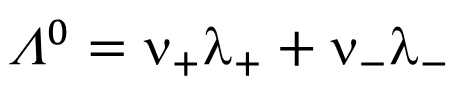
what does the limit of infinite dilution look like on a graph for strong and weak electrolytes

• strong → the electrolyte interactions that sloe down the conductivity as conc increases

• weak → the dissociation of ions is incomplete and its also a function of conc

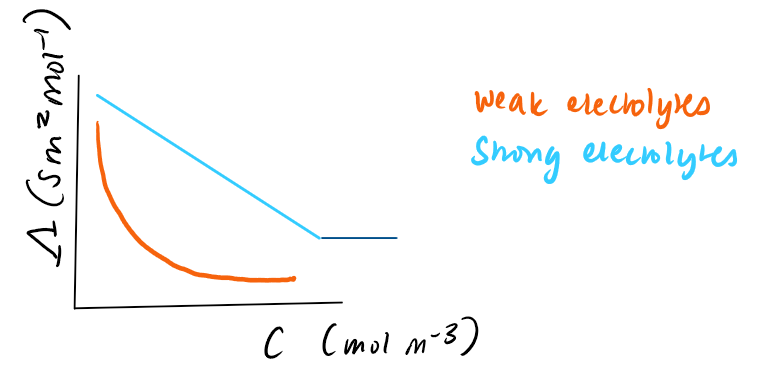
what can you work out with conductivity

• measuring the degree of dissociation of weak electrolytes

• limiting conductivity values relate to ion mobility

• relating ion mobility to effective size of ions in solution → the ion + solvation shell

osmotic pressure equation for non dilute solution (when xB bigger )

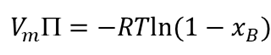
chemical potential of liquid solution that doesn’t behave ideally

γ = activity coefficient

m = molality mol kg-1

what does the activity of a solute aB tell us

• the effective molality of the solute → correcting for solute-solute interaction

• when RTlnγB = 0 the solution will be ideal → this would only be the case in very dilute solution

• in electrolytes the cations surround the anions forming ionic atmospheres → stabilising the solution

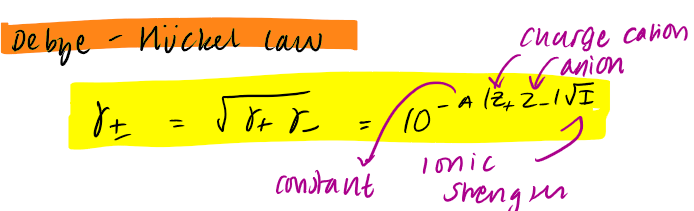
Debye-Huckle law - activity coefficient eq

unitless

ionic strength eq

unitless

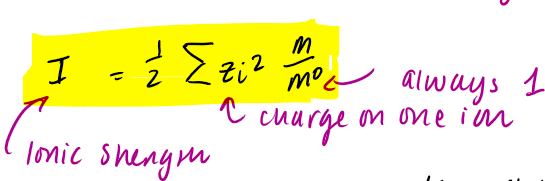
what does the Debye-Huckle law works for and what does it not work for

• works for low ionic strength / weak electrolytes

• deviates at higher Ionic strength due to ‘excluded volume’

• you’d need to modify the DH law to allow for

  • distance of closest approach → meaning it doesn’t account for the physical size of ions and treats them as point charges - as in the radius is 0

  • water of hydration bound to ions

  • ionic liquids - all conc electrolyte no solution

what’s a room temperature ionic liquid

• everything is an ion there is no solvent

• they’re a liquid because the ions are large AND they don’t pack easily

• have bad conductivity

what are 3 types of metals

1. conductors - band is not completely filled so it has accessible energy states for e-

2. semi-conductors - band gap is comparable to thermal energy so at certain T , some e- are promotes

3. insulators - band is full so no accessible states

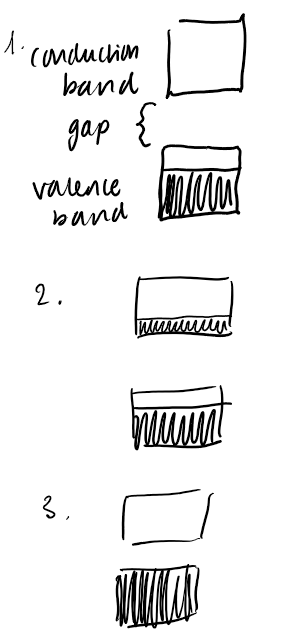
what is Fermi energy

• the top of the valence band where all the interactions happen

• it can be equated to chemical potential of the e- inside the solid

• the energy of the e- can be changed by applying external electrical potential φ

how does e- transfer work on orbitals and on the fermi energy

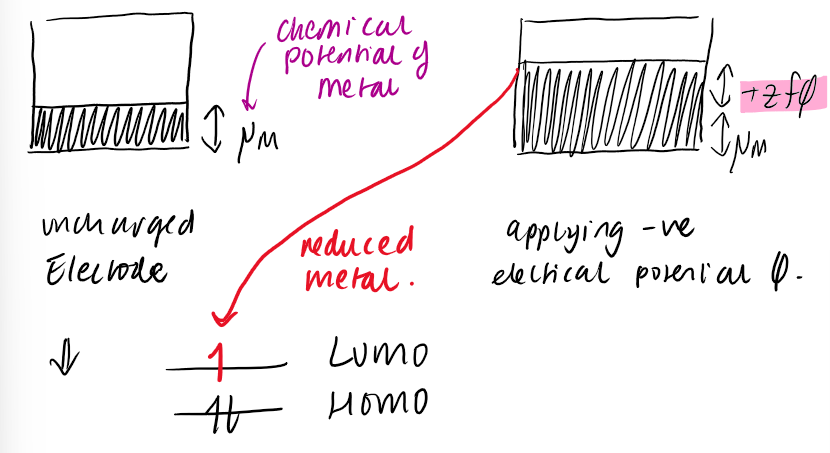
electrochemical potential eq

φ = electrical potential (V)

μ— = electrochemical potential = +ve

electrochemical potential eq of oxidised species

overall electrochemical potential equation that shows the electrochemical potential of the reaction = 0

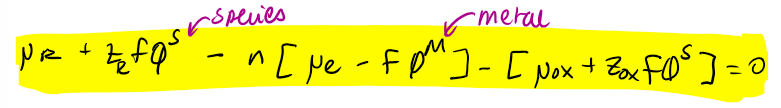
equation where chemical potential eq is substituted in electrochemical potential eq

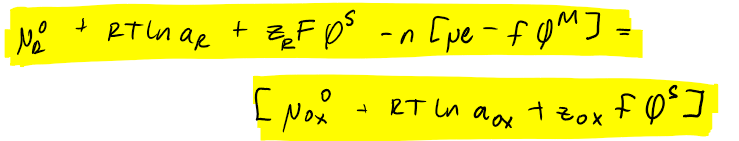
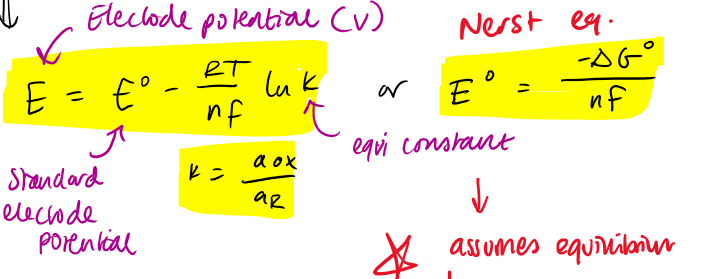
electrode potential + nerst eq

rearranged electrical potential equation that includes G

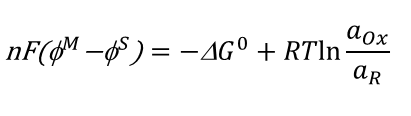
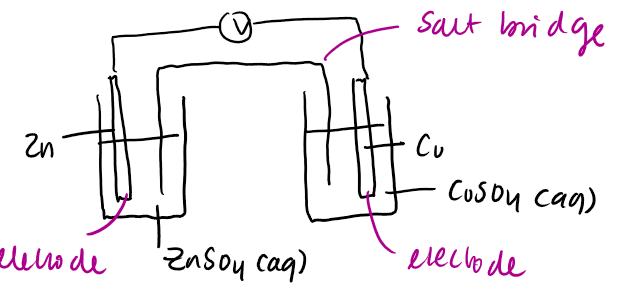
daniel cell eq

what does a Daniel cell look like

how would you write the system of a cell

• oxidation on the left

• reduction on the right

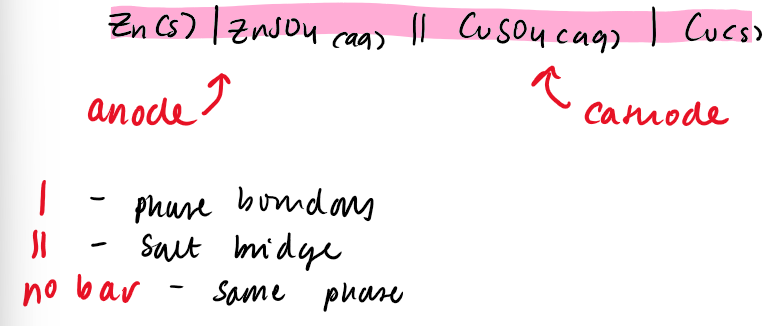
what is the reference redox couple

• the Hydrogen electrode (SHE)

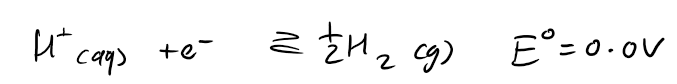
pH eq

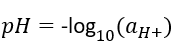
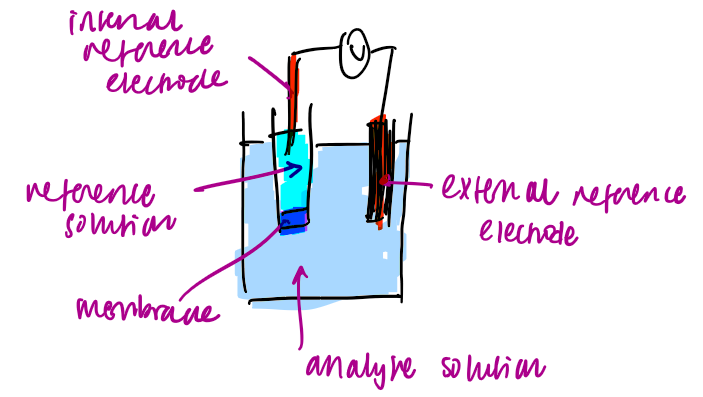
what does an ion selective electrode look like and what are the three phases

• the 3 phases

  • analyte solution

  • reference solution

  • membrane

• the target ion can go between all three

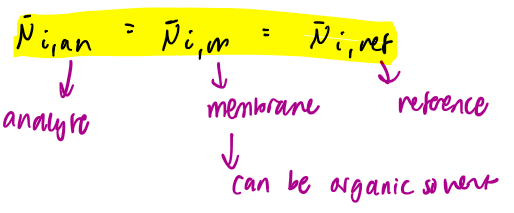
electrochemical potential of analyte in an ion selective electrode eq

ion transfer / electrical potential eq

• tells us the electrical potential required to drag ions into the membrane phase

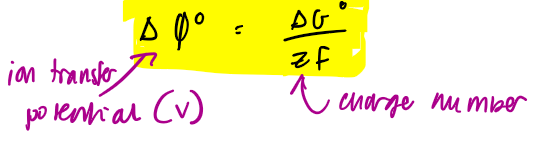
measured electrical potential difference eq

• shows us that the difference in electrical potential between the two electrodes φref and φan is proportional to the ratio of activities of the distributing ion in the phases

why store energy electrochemically?

1. thermodynamic limit on efficiency of combustion energy → electrochemical has a higher limit

2. greenhouse gas issues from combustion of hydrocarbons

3. increasing use of renewable energy

what are the 2 methods of storage of electrochemical energy

1. reversible conversion of chemical energy → electrical energy - secondary battery

2. irreversible conversion - primary battery ( can’t recharge)

what are the disadvantages of batteries

1. reactions not readily reversible - Zn2+ tends to form complexes that block contact between electrode and cathode

2. MnO2 is a poor electrical conductor - need inert carbon to transfer e-

3. heavy materials used - energy / mass ratio is low

4. cell voltage is limited to 1.4 -1.7V

what is the cathode and anode reaction on charging in non aqueous batteries

• lithium batteries

• the cathode and anode flip during discharging

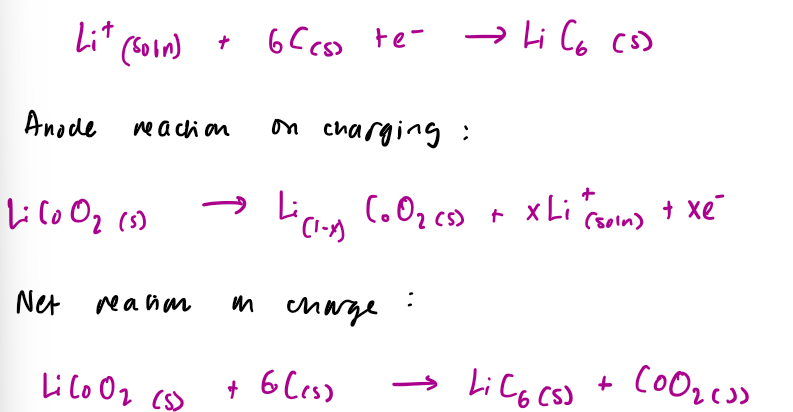
energy density eq for batteries

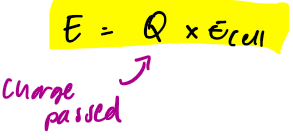
what are ideal battery characteristics

1. max energy density

2. reversibility

3. safe, non-toxic

4. light environments - use of Li

5. not reactive in H2O

what are disadvantages of Li batteries

1. organic solvent required - flammable, toxic

2. graphite intercalation used for prevention of formation of dendrites - dead weight

3. use of transition metal oxides - expensive , heavy

4. poor electrical conductivity

what’s the graphical shape of charge and discharge of Li batteries

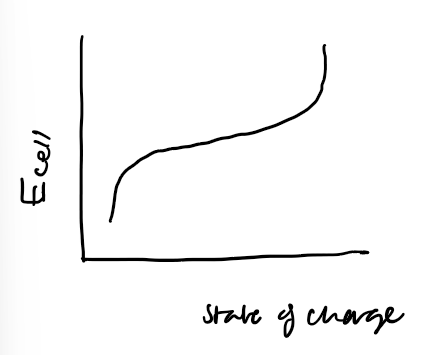
what’s the problem with the Nernst eq

• assumes equilibrium

• sets a theoretical potential that can be achieved

• we need to consider

  • kinetic loss

  • ohmic loss

  • conc loss