H2 Turnbull- Single-species populations I, II + III: Population growth and intraspecific competition, Population limitation and the determinants of population size, + Simple models in discrete time.

what are the different continuous models for population growth and what are their limitations?

linear function:

• N = mt + c

• dN/dt = m

• this means the population growth rate is independent of N, which isn’t sensible

• negative values are also possible

exponential model:

• N_t = N₀ e^rt

• dN/dt = rN

• this means the absolute growth rate is proportional to the population size, which is sensible

• exponential decay tends towards 0, so negative values aren’t possible

• 1/N dN/dt = r

• the per capita growth rate is constant, no matter how big the population gets, so this doesn’t account for environmental constrictions

logistic model:

• dN/dt = rN [(k-N)/k] where k is the carrying capacity of the environment, and r is the instrinsic rate of population increase

• this model gives exponential growth in small populations, which decreases to 0 nearing the carrying capacity, which is sensible

• 1/N dN/dt = r [(k-N)/k)]

• so when N is small, the per capita growth rate is equal to the intrinsic growth rate, but decreases linearly with increasing N

• this takes into account (negative) density dependence

• however this model is still basic

what determines r and k in population modelling?

r is the intrinsic growth rate, which is a life-history dependent trait (picture)

k is the carrying capacity (the maximum number of individuals that the environment can support)- this is not a life-history dependent trait

• however it is environment dependent- due to weather, acorn masting events etc

• k can then be made a random variable across a normal distribution

what is the discrete time logistic model?

• (the continuous time logistic model is dN/dt = rN [(k-N)/k])

• this is an iterative model, where the absolute growth rate = N_t+1 - N_t, and the per capita growth rate = (N_t+1 - N_t)/N_t

• this can be modified so that K is a variable across a normal distribution, rather than a constant, to account for environmental stochasticity

• this is a deterministic equation- if you know the values of N_t, k and r, you will obtain the same population prediction every time, which isn’t realistic

how does r affect the fluctuations in a population and its ability to recover from crashes?

• as r increases, the ability of a population to track/follow stochastic variations in the environment increases, so the population fluctuates much more

• species with low r are less affected by environmental stochasticity, and vice versa

• as r increases, the ability of a population to recover from catastrophic events increases

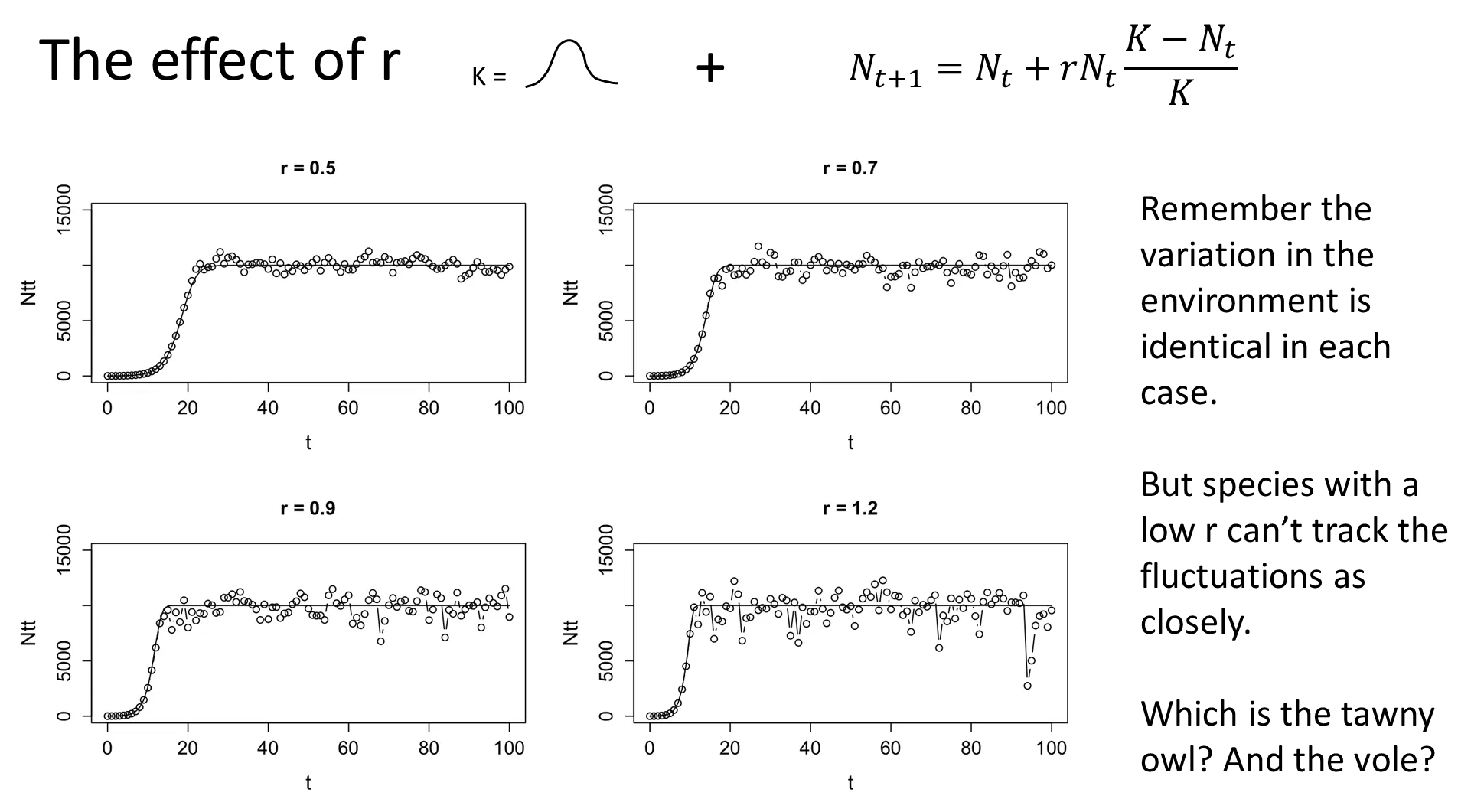
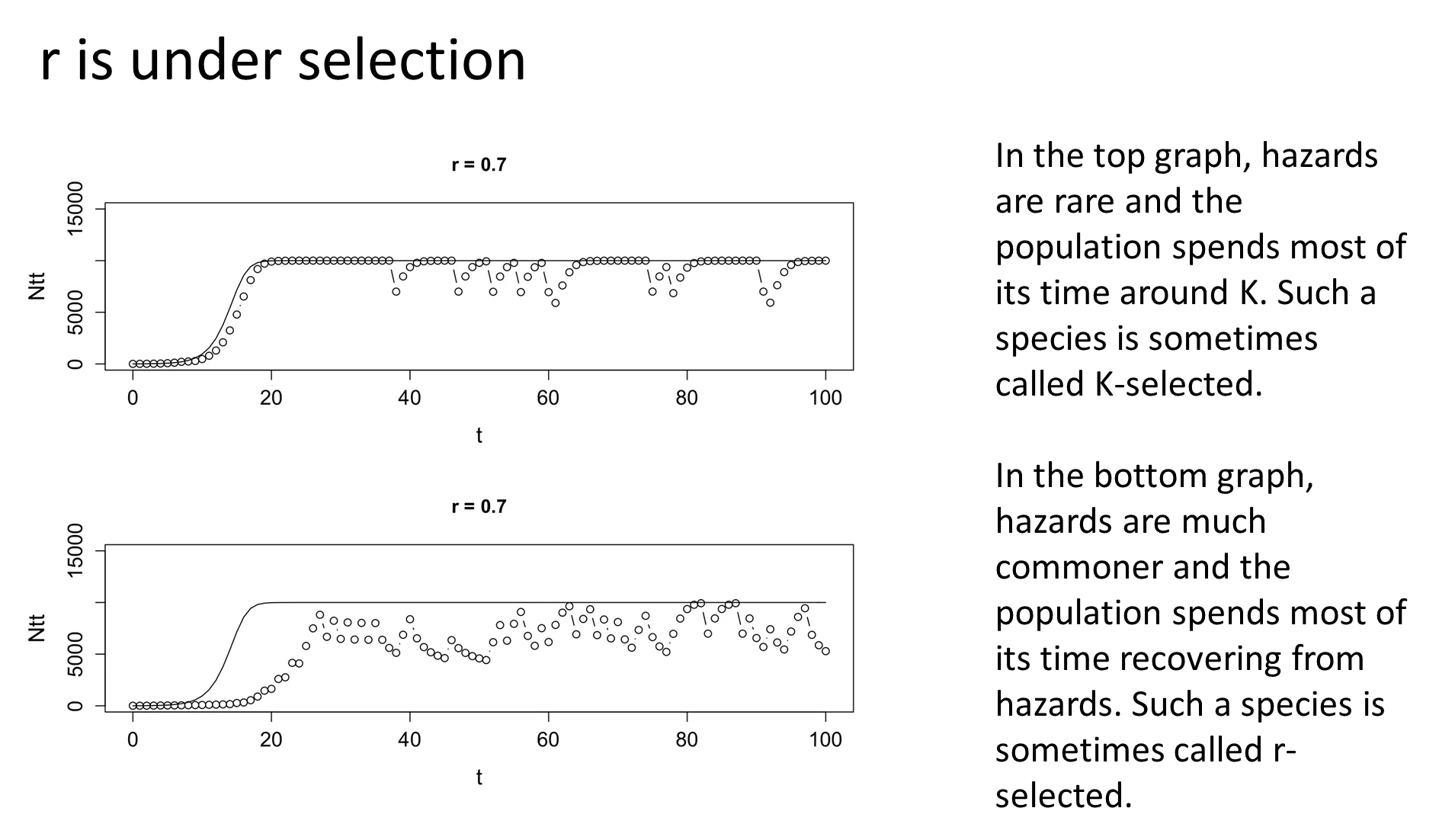
how do species evolve different r values?

• r is selected based on the environment a population is in

• when you live in a non-hazardous environment, your population is more dependent on stochastic variations of k, so a low r is favoured (k-selected):

  • resource competition favours large body size, late maturation and few, large offspring eg. seabirds, elephants + whales

• when you live in a hazardous environment, your population spends more time recovering from crash events, so a high r is favoured to bounce back faster (r-selected):

  • recovery phases favours small body size, large, frequent litters and early sexual maturity eg. rabbits + rodents

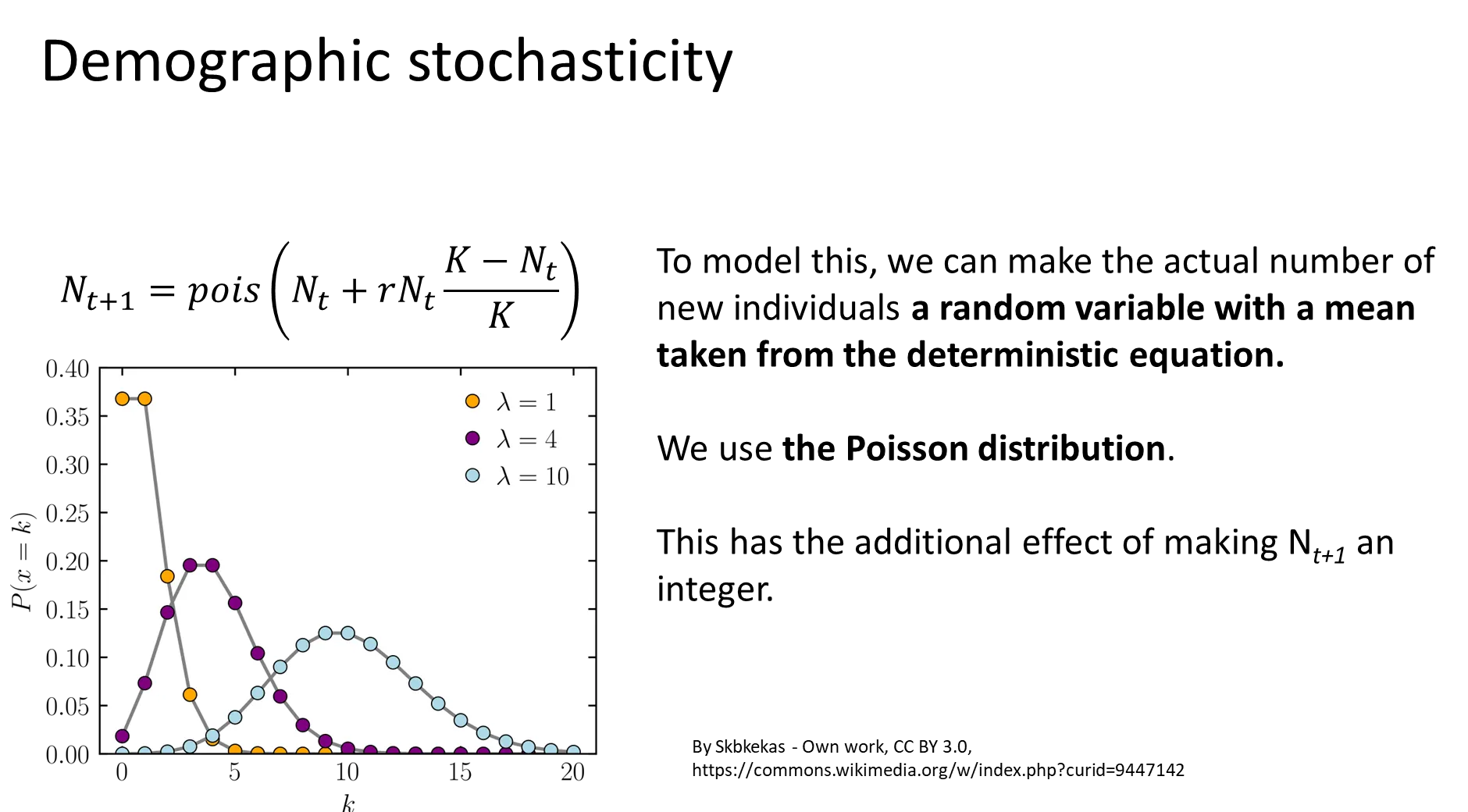
what is demographic stochasticity and why does it matter??

• demographic stochasticity is fluctuations in population size that occur because the birth and death of each individual is a random, discrete and probabilistic event eg. can’t have 1.5 children

• this is modelled by treating the number of new individuals as a random variable across a normal distribution, rather than as a deterministic quantity (so the same predictions won’t be attained each time)

• a poisson distribution is used, because the values are integers and can’t be negative (bounded at 0)

• the relative effect of demographic stochasticity is lower in large populations, but it is very influential in small populations, especially those with low r

• this type of randomness is endogenous to the population- it's not imposed by the environment

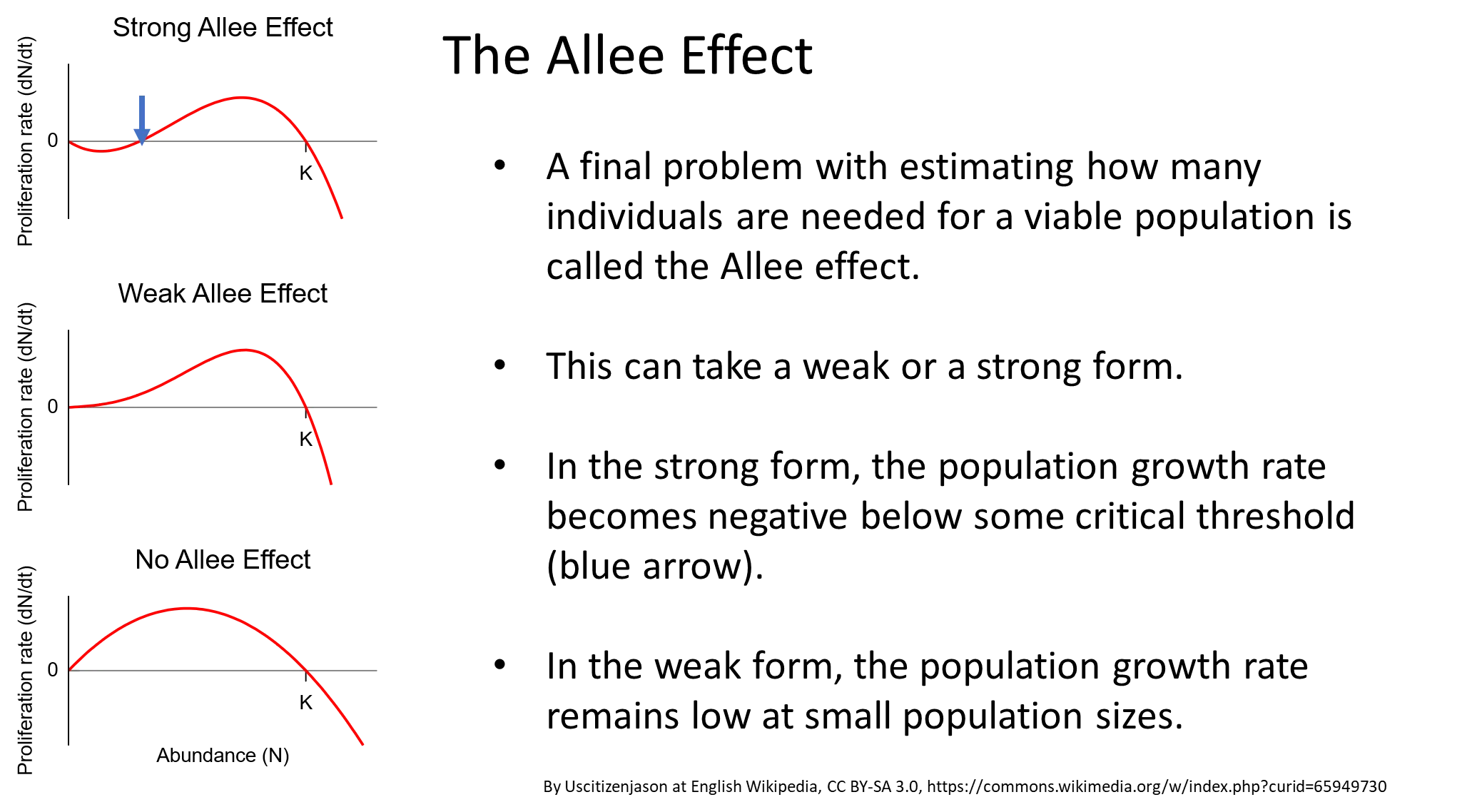
what is the allee effect? give examples

the allee effect states that special, hard to predict problems can occur in small populations, eg:

• musk ox- the herd forms a defensive ring around calves to fend off wolves, but when the population becomes too small, they can’t surround the calves properly

• african wild dogs- hunting is unsuccessful in small packs because they can’t attack prey that is much larger than they are, like usual

• kakapos- females will only be attracted to males when they are in groups

• when the allee effect is strong, the proliferation rate decreases, even to the point of causing negative growth rates

describe an example of a k-selected species

• the kakapo is a large flightless parrot from new zealand

• it is incredibly k-selected because it only breeds every 2-7 years, depending on masting years from its main food source, and adults live for decades

  • the introduction of mammals and hunting in new zealand devastated the populations

  • they were thought to have gone extinct, but a small island population was found, and intensive recovery programmes began, yet it is still under threat and vulnerable due to genetic erosion

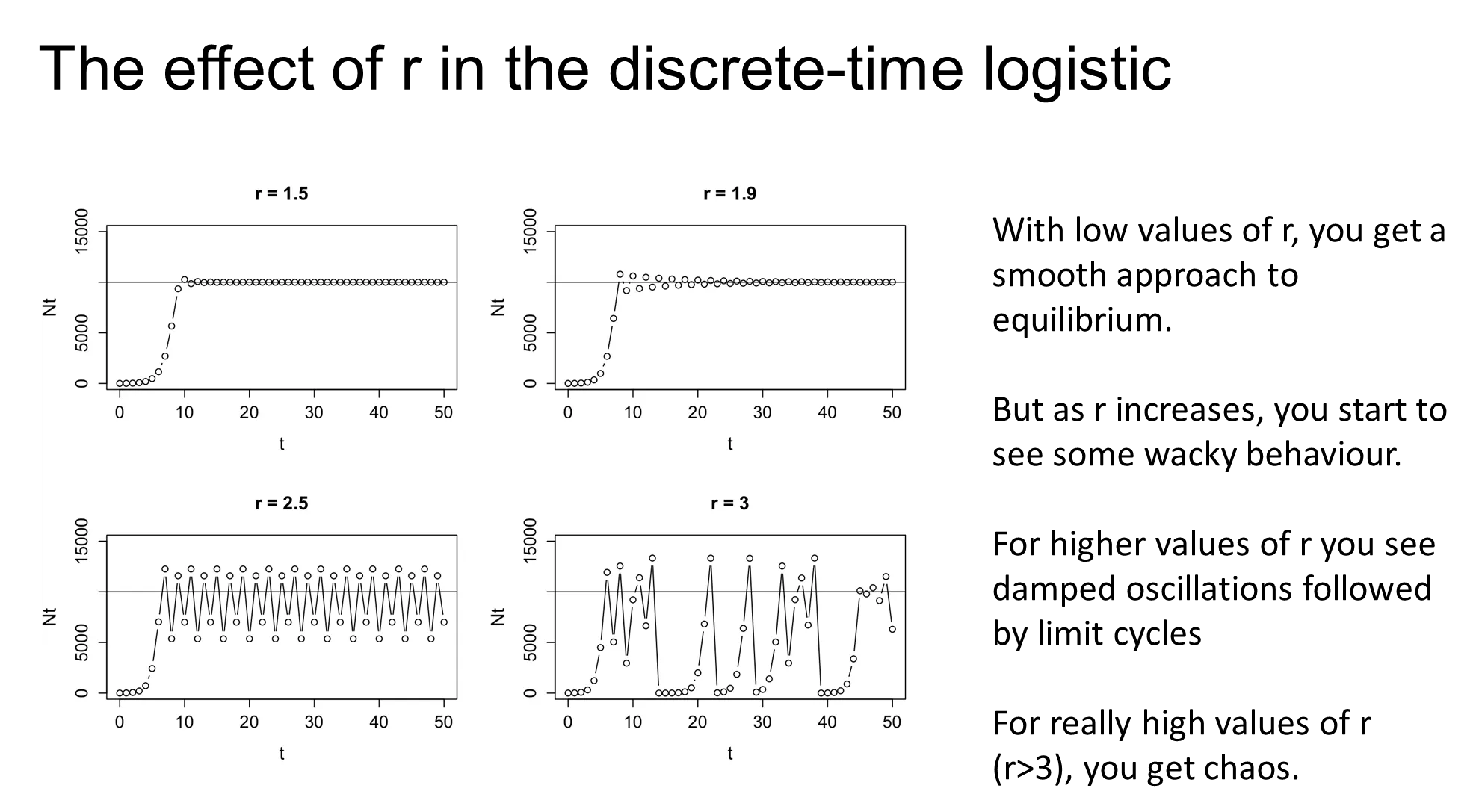
how do high r populations behave in a discrete time logistic model

• damped oscillations and limit cycles can happen in high r populations

• this is where the population is able to increase above the carrying capacity, which then brings the population right back down

• this is overcompensating density-dependence, which can cause catastrophic die offs

• in very high r populations, this causes chaos (deterministic not stochastic, but so unpredictable that it appears random)

this may not actually be present in real-life, it is just a phenomenon of the discrete time model