Vector Semantics

Word distributions: meaning and similarity

If A and B occur in similar environments then they probably have similar meanings. How words are distributed relative to other words can tell you about what they mean.

Why is word similarity helpful

question answering, google searching, exploring semantic change over time

How to model word distributions

Represent each word as a vector of numeric values, convenient to do mathematical operations on them, vectors can contain weighted counts or more abstract.

Sparse vectors

Derived from co-occurrence matrices, word-word matrix or term-document matrix. Values are counts or weighted counts. And contain a lot of zeros.

Dense vectors

values do not have a concrete meaning but represent a word’s location in semantic space, singular value decomposition, neural network inspired models.

Term document matrix

You have a bunch of documents you are interested in. Count how many times different words appear in each document. Words that appear in the same documents and don’t appear in the same documents are likely to be related. Documents that have the same words might be about similar or related topics.

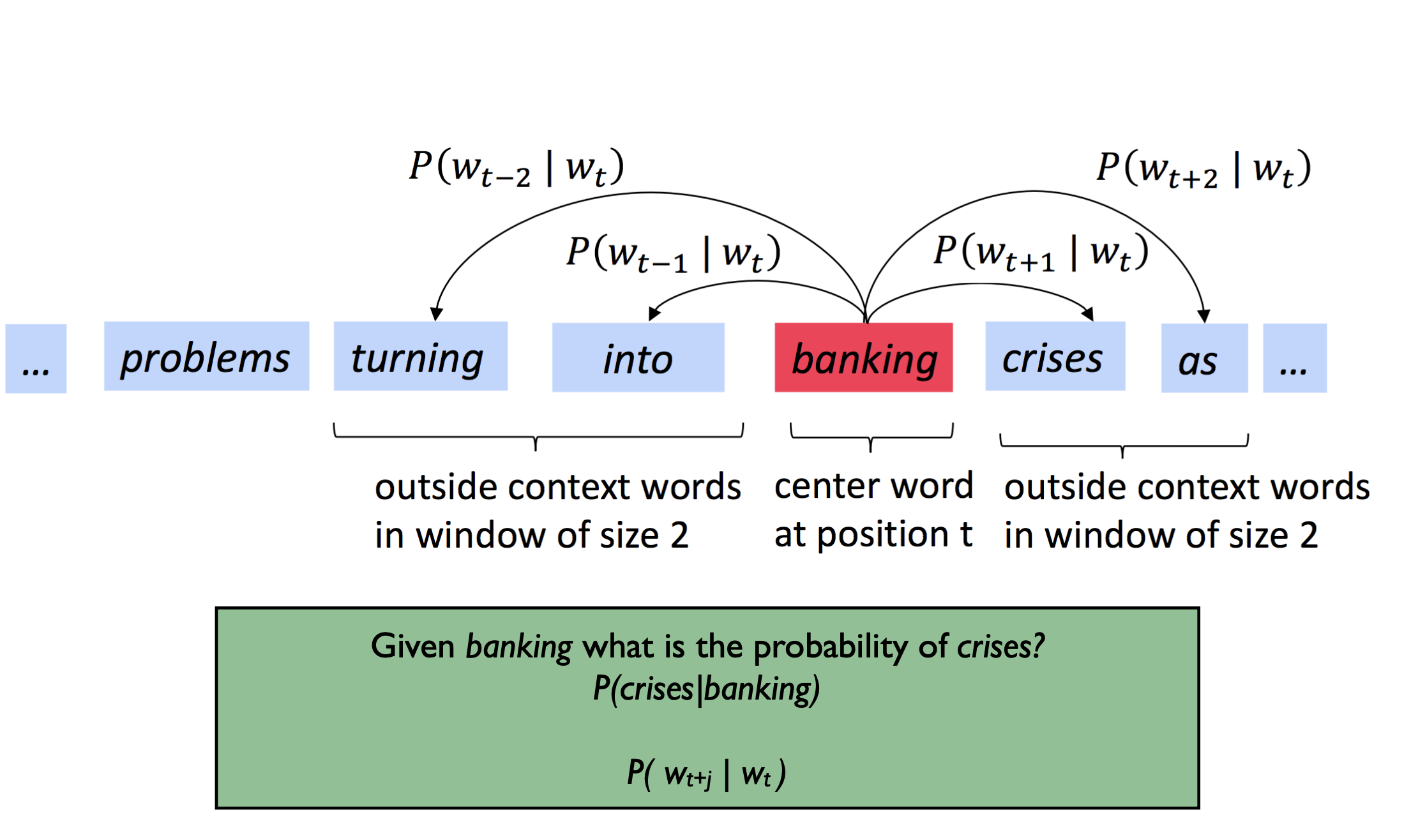
Word-word co-occurrence matrix

Step1: get a huge corpus of text

Step 2: Count how often each word co-occurs (eg appears in the same five word window) with each other word. You end up with a |V| x |V| matrix where V is the vocabulary which contains 10s or 100s of 1000s of words. Every word has a vector of |V| values most of which are zero. You can compare the vectors with cosine similarity.

Comparing vectors: cosince similarity

Two docs or words are similar is their vectors are close together. A vector is close to another if the angle is small and hence the cosine of the angle between them is large.

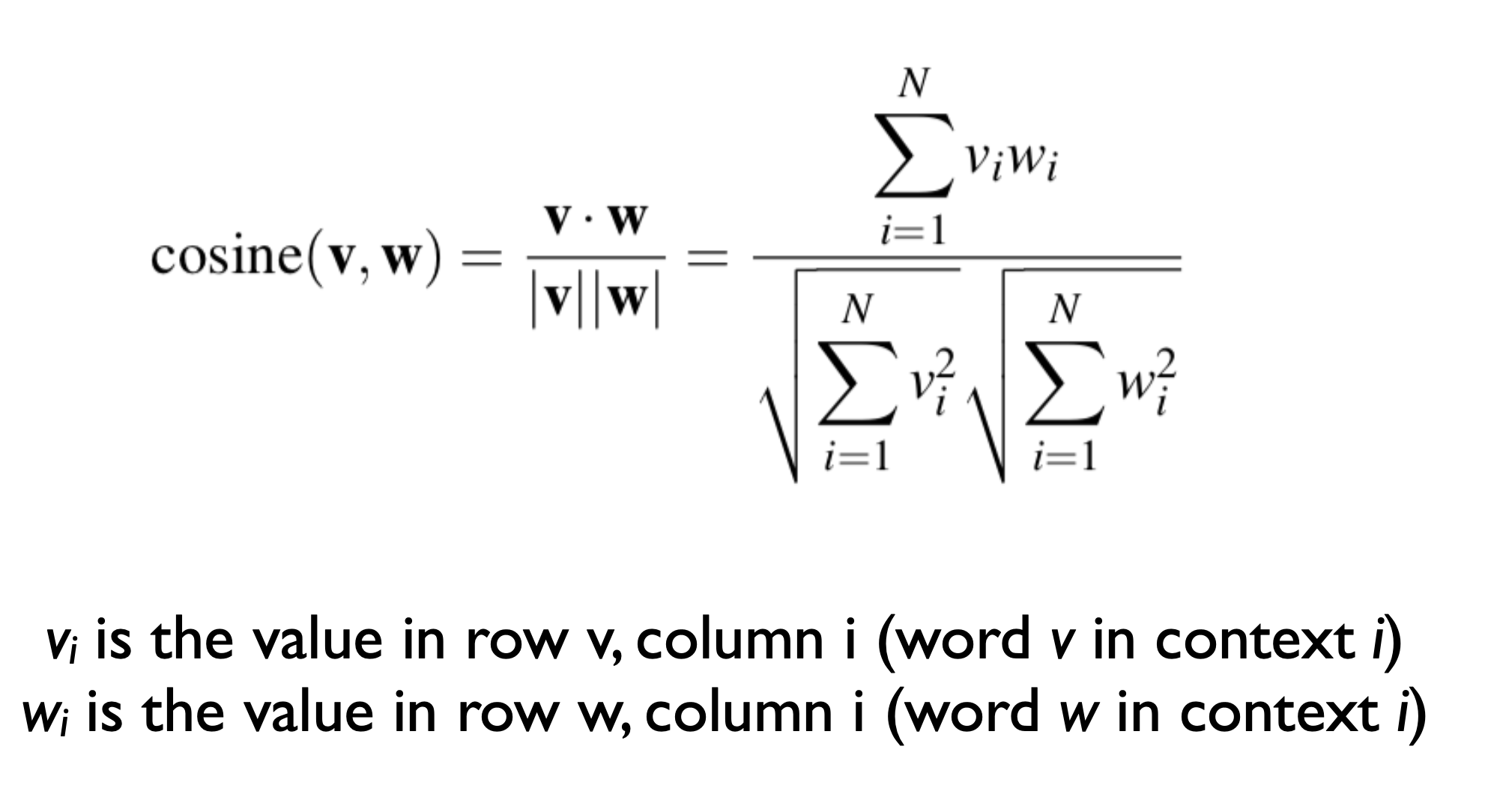
Other similarity metrics

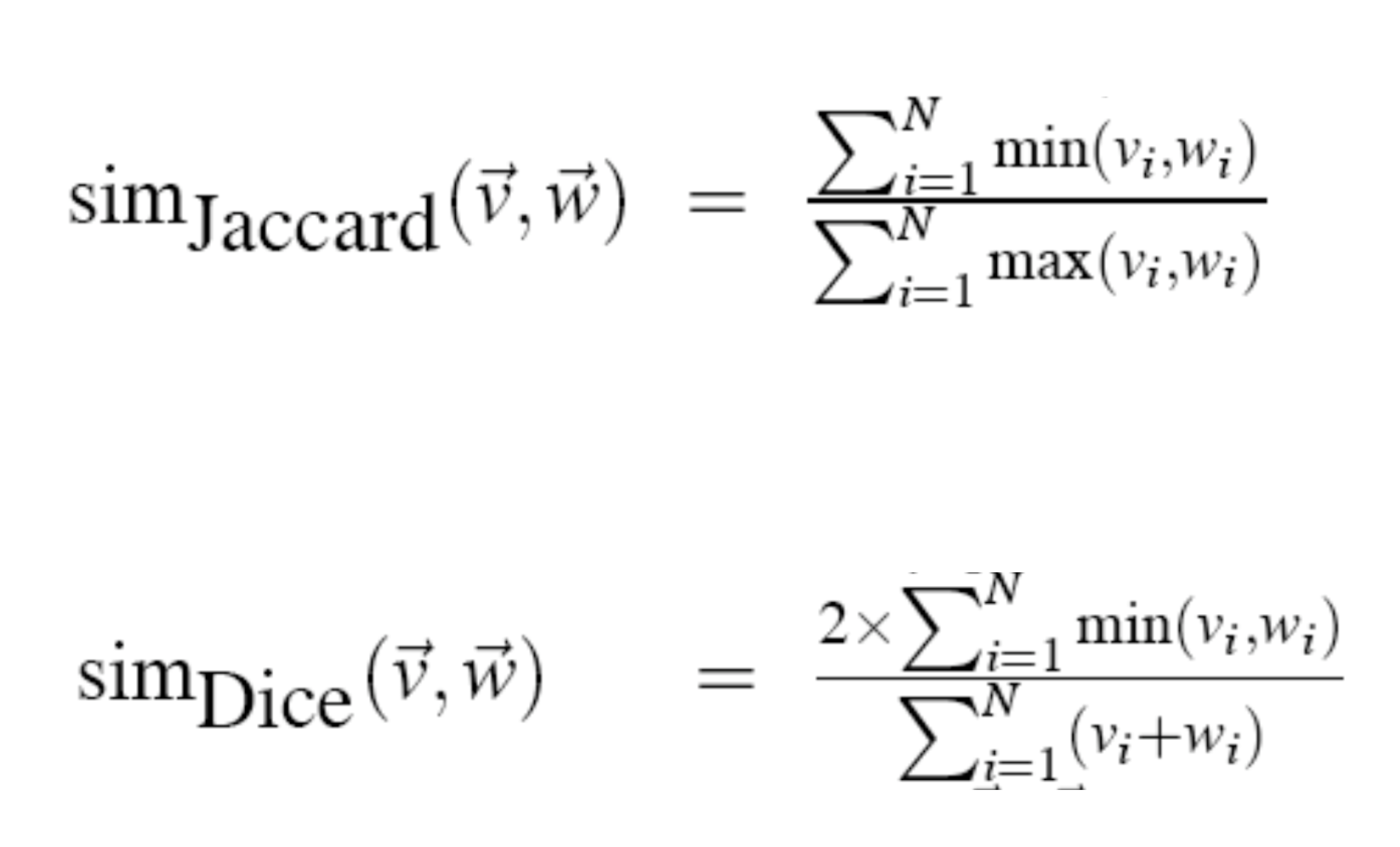
PMI

Pointwise mutual information can also go into the matrix. PMI calculation do x and y co-occur more than if they were independent? Problem with PMI is negative values do not correspond to dissimilarity, so if it is negative just say it is zero and get PPMI.

Step1: Turn counts into probabilities

Step 2: Using probabilities calculate ppmi for each cell

Step 3: Now use these vectors to see how close two words are like cosine similarity

tf-idf

In term document matrix you can replace counts with a normalized version of that count. tf-idf is term frequency inverse document frequency. Divide the count by the number of documents this word appears in. Normalize counts like this because some words appear often in all documents, dividing by the number of documents the word appears in gives this words much less weight.

Sparse vs Dense vectors

sparse: many dimensions (10K-100K) and many zeros

dense: fewer dimensions (100-1000), most elements are not zero

Advantages of dense vectors

Easier to use as features in ML since there are fewer features. Only 100-1000 values to store each word, fewer dimensions lead to faster math.

How do you get dense vectors

Single value decomposition (SVD) : latent semantic analysis LSA

Nerual predictive models: continuous bag of words, skipgrams, word2vec, skipgrams

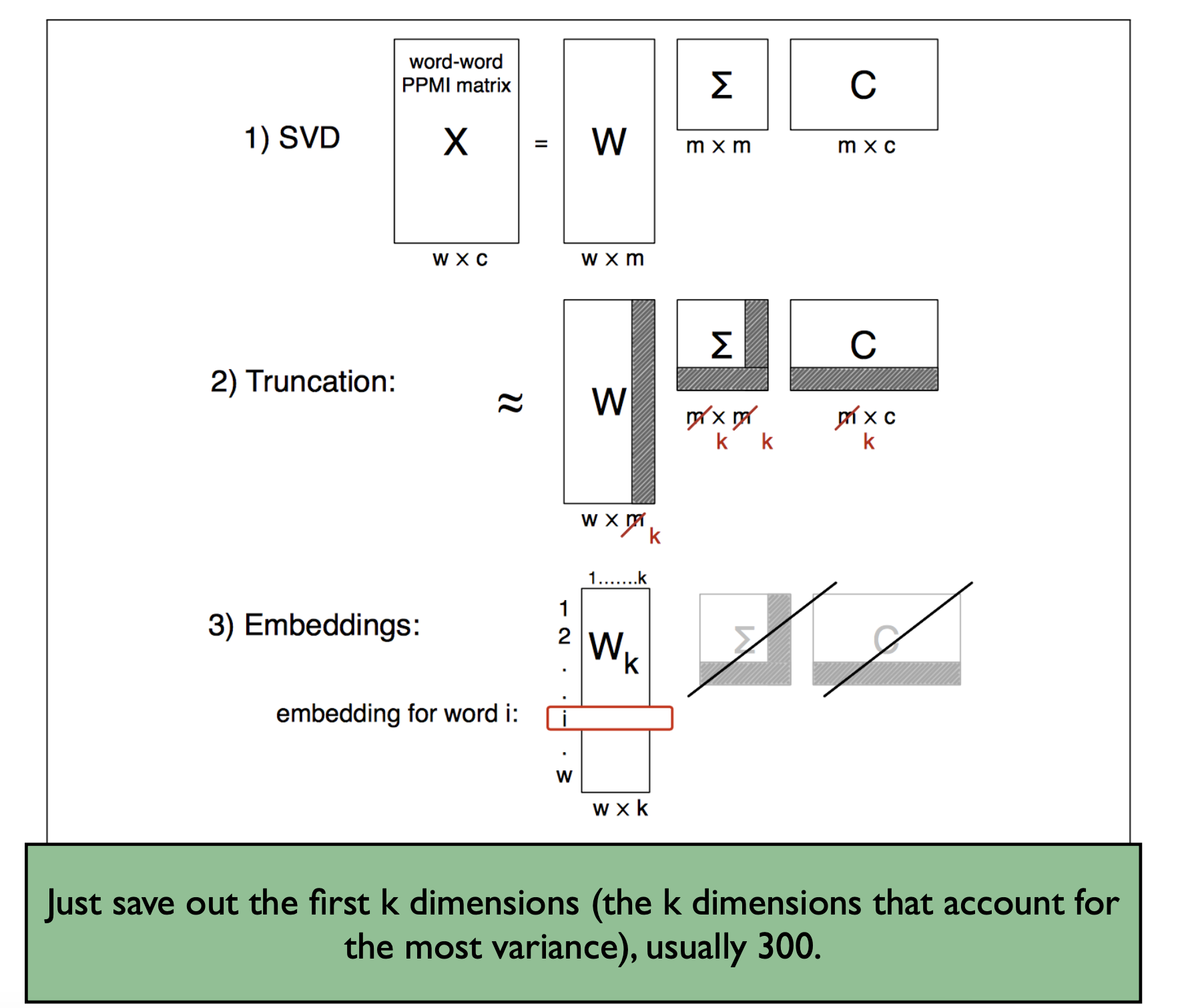
SVD

Goal is to reduce the number of dimensions. It is a family of methods for dimensionality reduction which include principal component analysis (PCA) and factor analysis. Start with full term document matrix or word-word co-occurrence matrix. Rotate the matrix to where you find the dimension that accounts for the most variability. Rotate again to find the dimension that counts for second most variability and so on.

Neural word embeddings

Don’t actually build a term-term co-occurrence matrix. Instead build neural net classifier that determines the best word given a particular context. Words that have a similar context are likely to be similar in some way .