Unit 2 | Chapter 3: Logic

Statement

A sentence that is either true or false, but not both simultaneously.

Commands, questions, or opinions.

Statements are not…

Simple statement

A statement that conveys one idea with no connecting words.

Compound statement

A statement formed by joining two or more simple statements with a connective.

Connectives

Words used to join simple statements. (Ex: and, or, if...then, and if and only if.)

Quantifiers

The words all, some, and no (or none).

Universal quantifiers

Words used in statements that either include or exclude every element of the universal set.

• All, each, every, no, none

Existential quantifiers

Words used in statements that claim the existence of something, but don't include the entire universal set.

• Some, there exists, at least one

Statement negation

Where a statement has the opposite meaning, as well as the opposite truth value, from the given statement.

• Represented by ~

• Not/no.

• A true statement becomes a false statement, and a false statement becomes a true statement.

• The least dominant connective

The statements: Some A are not B

Or, Not all A are B.

negates…

The statements: All A are B

Or, There are no A that are not in B.

negates…

The statements: No/None of A are B

Or, All A are not B.

negates…

The statements: Some A are B

Or, There exists at least one A that is a B.

negates…

Conjunction

A compound statement that is true only when both simple statements are true.

• Represented as ∧

• And

• p and q

• A 3rd most dominant connective

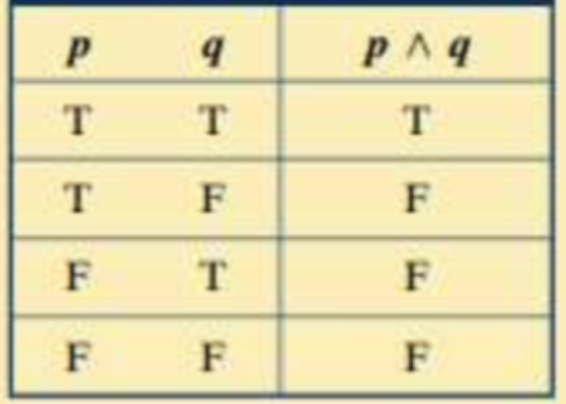
Conjunctions in a truth table are…

Always false, except when T∧T and is true.

And

Refers to the conjunction of compound statements.

Disjunction

A compound statement that is false only when both component statements are false.

• Represented by ∨

• Or

• p or q or both

• A 3rd most dominant connective

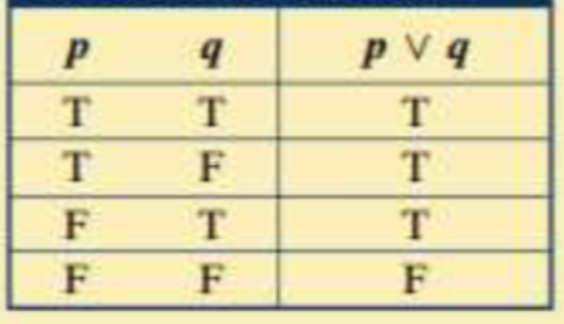
Disjunctions in truth tables are…

Always true, except when F∨F and false.

Or

Refers to the disjunction of compound statements.

Conditional statements

A compound statement that is false only when the antecedent is true and the consequent is false.

• Represented by →

  • Is only true/good one way (→), and will be false the other way.

• If... then.

• "If p, then q" or “p implies q”

• -Antecedent → Consequent

• The 2nd most dominant connective

Conditionals in truth tables are…

Always true, except when T→F and is false.

Antecedent

The statement in a compound statement that is before the →.

Consequent

The statement in a compound statement that is after the →.

Biconditional statements

A compound statement that is true only when the component statements have the same truth value.

• Represented by ⟷

  • Is true/good both ways

• If and only if. (abbr. iff)

• "p if and only if q"

• The most dominant connective

Biconditionals in truth tables are…

Always false, except when T⟷T or F⟷F and is true.

the statements in parentheses appear on the same side of the comma.

• Ex: If q and ~p, then ~r

  • (q ∧~p) → ~r

In English simple statements,

Dominance of Connectives

If a symbolic statement appears without parentheses, statements before and after the most dominant connective should be grouped.

• Biconditional>Conditional>Conjunction and Disconjuntion> Negation

Tautology

A compound statement that is always true.

Equivalent compound statements

Compound statements that are made up of the same simple statements and have the same corresponding truth values for all true-false combinations of these simple statements.

then its equivalent statement must be true.

If a compound statement is true,

then its equivalent statement must be false.

If a compound statement is false,

The two parts of an argument

• Premsies/assumptions

• Conclusion

Premisies/Assumptions

The given statements in an argument.

Conclusion

The result determined by the truth of the premises within an argument.

Valid argument/Tautology

The conclusion is true whenever the premises are assumed to be true.

Invalid argument/Fallacy

An argument that is not valid, or has at least one false in its truth table.

Steps for testing the validity of an argument with a truth table

1. Use a letter to represent each simple statement in the argument.

2. Express the premises and the conclusion symbolically.

3. Write a symbolic conditional statement of the form [(premise1)∧(premise2)∧...∧(premise n)] → conclusion, where n is the number of premises.

4. Construct a truth table for the conditional statement in step 3.

5. If the final column of the truth table has all trues, the conditional statement is a tautology and the argument is valid. If the final column does not have all trues, the conditional statement is not a tautology and the argument is invalid.

[(premise1)∧(premise2)∧...∧(premise n)] → conclusion, where n is the number of premises.

The symbolic form of an argument and its conclusion