semantics exam #2

antonymy

a relationship of incompatibility between 2 terms w/ respect to some given dimension of contrast

gradable antonymy

has a midpoint

ex: hot → lukewarm → cold

non-gradable antonymy

does not have a midpoint

ex: pass/fail, dead/alive

meronymy

- the relation of part to whole

- 6 diff types

-one of the properties is that it is transitive

6 types of meronymy

1. component-integral object (ex: pedal/bike)

2. member-collection (ex: ship/fleet)

3. portion-mass (ex: slice/pie)

4. stuff-object (ex: steel/car)

5. feature-activity (ex: paying/shopping)

6. place-area (ex: Everglades/Florida)

transitivity

when the same type of meronymic relation is involved in all parts of the chain

ex:

A seed is part of a fruit.

A fruit is part of a plant.

A seed is part of a plant.

hyponymy

- a hierarchy of elements

- associated with the phrases: kind/type/sort of

-Hyponym – a lower term in a hyponymic hierarchy

•ex:

A sports car is a hyponym of car

A car is a hyponym of vehicle

- Hyperonym – a higher term in a hyponymic hierarchy

• A vehicle is a hyperonym of car

• A car is a hyperonym of sports car

synonymy

when two words have the same meaning in a given context

ex: smile/smirk

monosemy

a word that has only one sense

ex: adverb, cassette

polysemy

a word that has more than one distinct sense (usually semantically related)

ex:

date

• day of the month specified by a number

• social or romantic appointment

chair

• furniture for an individual to sit in

• head of a committee

syllogism

an argument in which a conclusion is deduced from premises

ex:

1. All cats like reality television.

2. Ron is a cat.

therefore

3. Ron likes reality television

premise

an argument’s starting-point; a proposition from which the conclusion follows

conclusion

a proposition deduced from premises by an argument

universal quantifier

all – ∀

a predicate is true of every entity in the domain under discussion

• all, every, each and every, everything

existential quantifier

some – ∃

a predicate is true of at least one entity in the domain under discussion

• some, at least one, something

entailment

the truth of the first proposition guarantees the truth of the second

presupposition

A proposition p presupposes another proposition q if both p and the

negation of p entail q

is true even when its trigger is false

ex:

Bonnie recently stopped smoking

Bonnie was a smoker

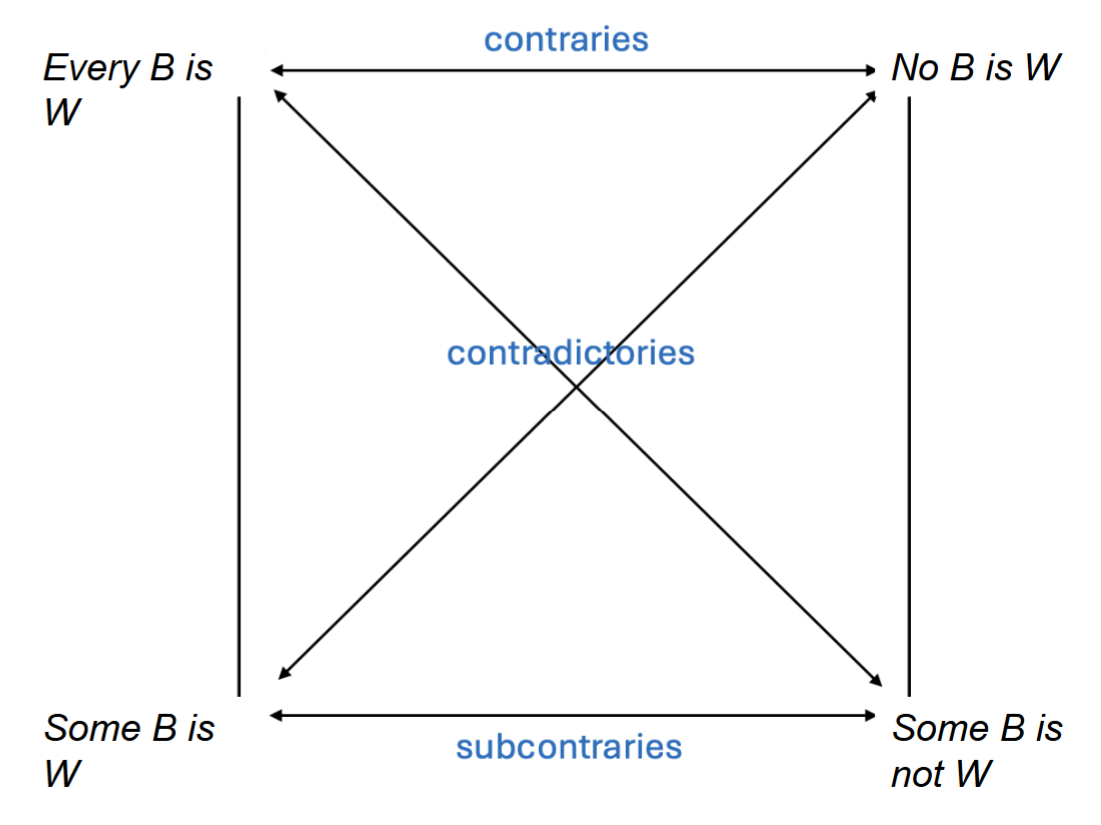
Contradictory

If one proposition is true, the other must be false; & vice versa

ex:

(1a) Titanic won Best Picture in 1998.

(1b) Titanic did not win Best Picture in 1998

Contrary

Two propositions can both be false at the same time but they cannot be simultaneously true

ex:

(1a) Maria is happy.

(1b) Maria is sad.

subcontrary

Two propositions can both be true at the same time but they cannot be simultaneously false

ex:

(1a) Some people are happy.

(1b) Some people are not happy

square of opposition

valid & sound argument

the premises are true

valid & unsound argument

at least one of the premises is false

invalid argument

the conclusion of an argument cannot logically be derived from the premises

negation operator

not - ¬

a sentence contains denial or negation

ex:

p Glinda is telling the truth.

¬p Glinda is not telling the truth

conjunction operator

denotes the union, or conjunction of two propositions - &

and, but, although, in spite of

ex:

p Elphaba is the Wicked Witch.

q Glinda is the Good Witch.

p & q Elphaba is the Wicked Witch, [conj.] Glinda is the Good

Witch.

exclusive disjunction operator

only one of the disjuncts applies, but not both

Symbol: X-OR

ex:

Jim loves Pam or Karen (but not both).

p Jim loves Pam

q Jim loves Karen

p X-OR q

inclusive disjunction operator

both of the disjuncts applies - V

ex:

People were wearing hats, or they had put on sunscreen.

• There is the possibility that some people were wearing both hats and

sunscreen → inclusive

p People were wearing hats

q People had put on sunscreen

p ∨ q

material conditional operator

corresponds roughly to if...then - ⊃

ex:

If there’s no one at the counter, then the museum is closed.

p There’s no one at the counter (antecedent)

q The museum is closed (consequent)

p ⊃ q

one-place predicate

predicates with one argument

can only be associated with one single variable at a time

ex:

Ron (r) is a cat (C)

Cr

two-place predicate

predicates with two arguments

ex:

Ron fought Harry

• F – ‘to fight’

• Fr, h

three-place predicate

predicates with 3 arguments

ex:

Tina (t) gave (G) the book (b) to Linda (l)

Gt, b, l

individual constant

the individual entity which the constant picks out in the world

ex:

h, s, g, p

h = Henry

s = Shannon

g = Gabriela

p = Patrick