propositional logic I syntax

propositional logic

the branch of logic that studies the relationship and combination of propositions

propositions

a simple declarative statement that can be either true or false, it must be one or the other and not both

examples of propositions

• the lights are on

• there is a logic class at ifm

• macron is the french president

how to determine whether p is a proposition

• use the technique “is is true that p”

• if the resulting sentace is grammatical, then p is a proposition

atomic proposition

the truth of falsity does not depending on the truth or falsity of any other propostion

examples of atomic proposition

the lights are on, theres a logic class at ifm, macron is the french president

compound propositions

built by combining atomic propositions with logical connectives

examples of compound propositions

• the lights are on and there is a logic class at ifm

• there is not a logic class at ifm

• macron is the french prime minister or macron is the french president

• either we use this new ad campaign or we do not use this new ad campaign and we loose a lot of money

¬

not, negation

∧

and, conjuction

∨

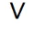
or, disjunction

→

implied, conditional

p↔q

if and only if, true when p and q have the same truth value

syntax

defines the syntactically acceptable objects of the language, also called well formed formulas

well formed formulas

• propositional letters

• if p is a formula, then ¬p is too

• if p and q are formulas, then p∧q, p∨q, p→q and p↔q are formulas

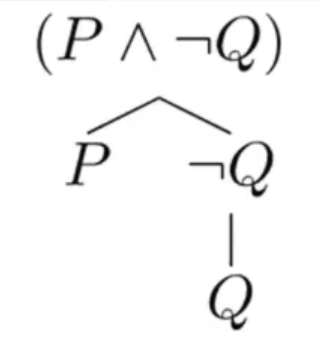
construction tree

each logical formula can be visually represented by a unique construction tree

conditional statement

• statement of the form “if p, then q” where p is called the anteccedent and q is called the consequent

• anything follows from a false statement

• so long as the anteccedent is fale, the conditional is true regardless of the truth value of the consequent

biconditional

A statement of the form “PPP if and only if QQQ,” asserting that PPP is true exactly when QQQ is true—that is, each is both necessary and sufficient for the other.

examples of a true biconditional

p = x is a triangle

q = x has exactly three sides

• (p → q) = if x is a triangle, then x has exactly three sides TRUE

• ( q → p) if x has exactly three sides, then x is a triangle TRUE

• so (p ↔) is TRUE

examples of false biconditional

p = x is a triangle

q = x is a geometrical shape

• (p → q) = if x is a triangle, then x is a geometrical shape TRUE

• ( q → p) if x is a geometrical shape , then x is a triangle FALSE

• so (p ↔) is FALSE

translations

translate sentances expressed in natural language in propositional logic

• for each translation, you need to provide a key

• the key explains what propsotions your propositional letters stand for

examples of translations

1. if i wakeup early, ill go to the gym ( p>q),

key; p= i wakeup early and q= i will go to the gym

2. if i wakeup early and i go to the gym, ill feel good unless i miss my bus

key; p= i wakeup early, q= i will go to the gm, r= i will feel good, s= i miss my bus, ¬s= i dont miss my bus

translations into natrual languages

propositional logic helps remove ambiguities present in natrual languages