Análisis matemático 2
1/14
Earn XP
Description and Tags
Name | Mastery | Learn | Test | Matching | Spaced | Call with Kai |
|---|
No analytics yet
Send a link to your students to track their progress
15 Terms
Continuidad (demo)

La demo se divide en dos partes.
1) consideramos a r continua en t0 y tomamos que el lím r(t)= r(t0). Buscamos llegar a que la igualdad del límite se cumple para todas las funciones componentes de fi.
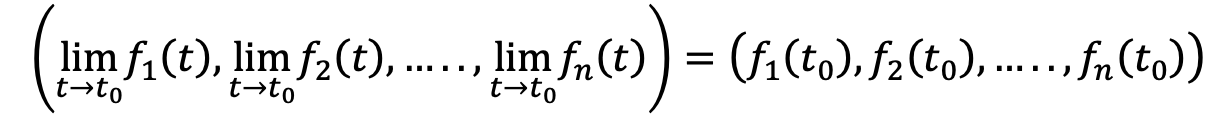
2) suponemos que las funciones componentes fi son continuas en t0. Buscamos llegar a que el lím r(t)= r(t0).
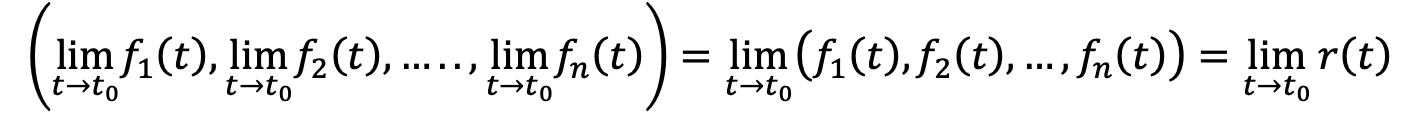
Longitud de arco (demo)

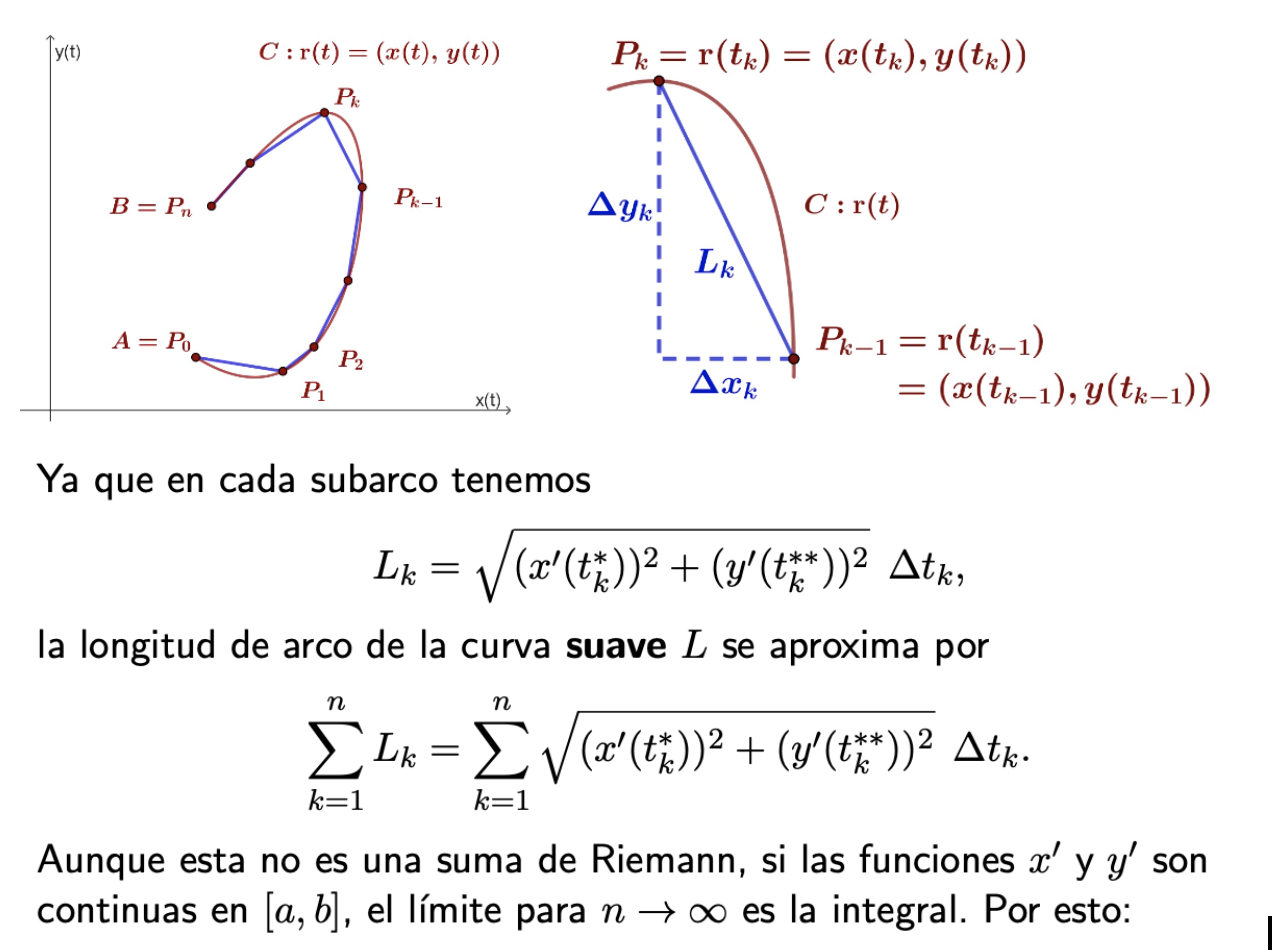
Buscar la partición del intervalo, aproximar la longitud del arco con la distancia Lk, buscar la relación con el Teorema del valor medio y usar sumas de Riemann para calcular la integral en el límite.
Derivada parcial
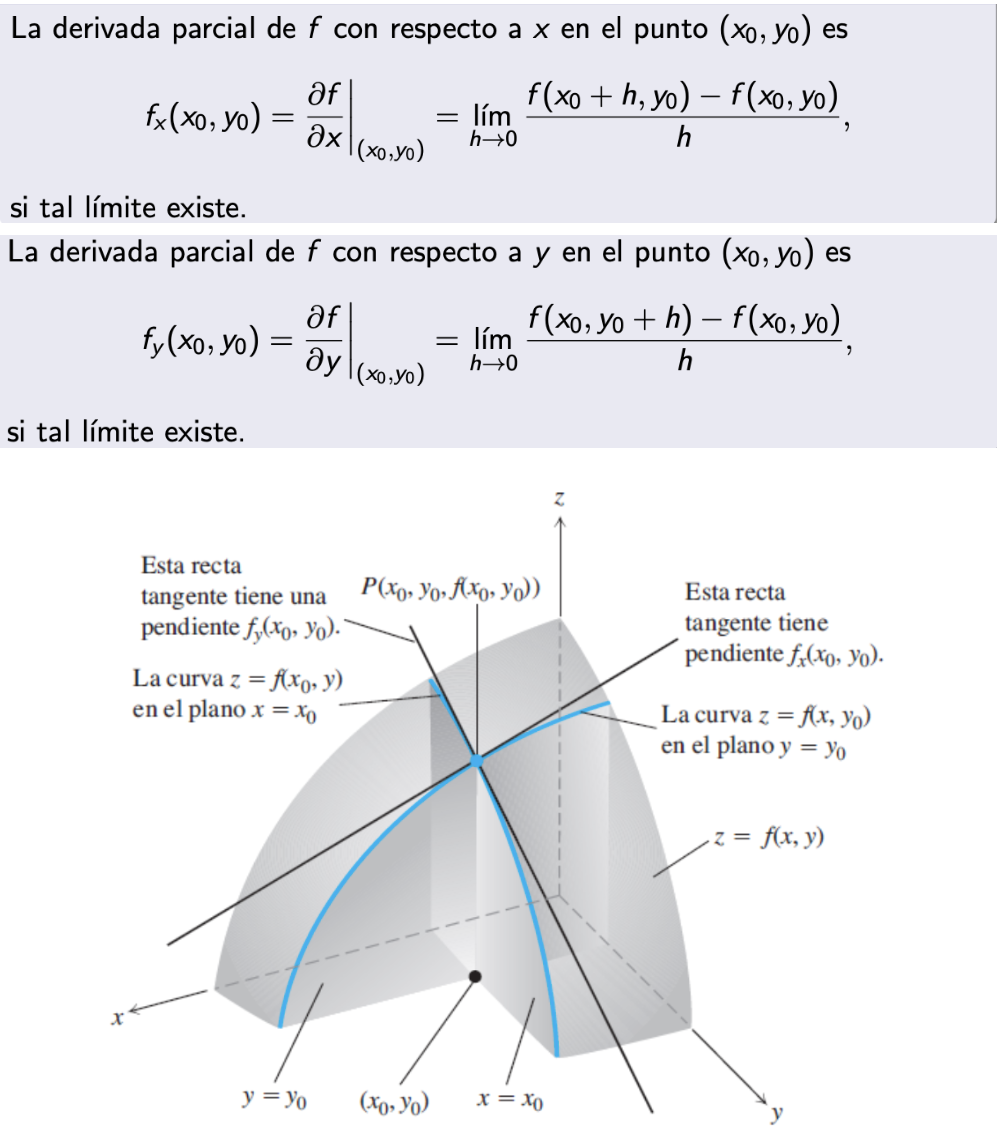
Es la razón de cambio de la función, en el caso de fx en dirección de i y para fy de j. Las rectas tangentes con pendiente fx y fy forman un plano tangente a la superficie.
Diferenciabilidad

La diferenciabilidad de una función en un punto implica que tiene derivadas parciales en ese punto y que se puede aproximar mediante un plano tangente en una vecindad de dicho punto.
Diferenciabilidad implica continuidad (demo)

Teorema del incremento (demo)

La función f con el teorema de Valor medio, por lo que f(x0 +∆x,·) es derivable en el intervalo [y0,y0 +∆y] y existe un valor d en el intervalo tal que
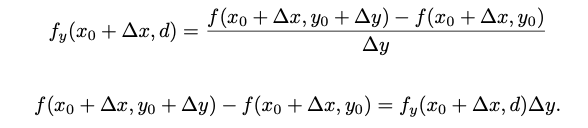
Obtenemos una expresión equivalente a los dos primeros términos. De manera análoga, tomamos la función f(·,y0) y existe un valor c en el intervalo (x0,x0 +∆x) tal que
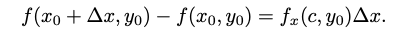
Sustituimos en la 1ra expresión

Sustituimos nuevamente y llegamos a la definición de función diferenciable. Nos queda probar que los errores tienden a cero cuando (∆x, ∆y) → (0, 0). Aplicamos la continuidad de las derivadas parciales que tenemos por hipótesis y aseguramos que
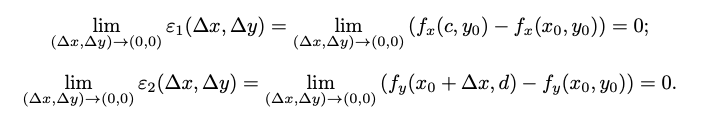
Regla de la cadena (demo)

Consiste en mostrar que si 𝑥 y 𝑦 son derivable en 𝑡 = 𝑡0, entonces w es derivable en 𝑡0

Derivación implícita R2 y R3 (demo)


Se demuestra bajo supuesto, tomamos la función con la igualdad a c y derivamos en función a x usando a la regla de la cadena. Reccordamos que dx/dx=1 y despejamos y´(x).
En el caso de R3, aplicamos el mismo procedimiento, utilizando las componentes adecuadas y derivando parcialmente en función a ambas variables por separado.
Derivada direccional
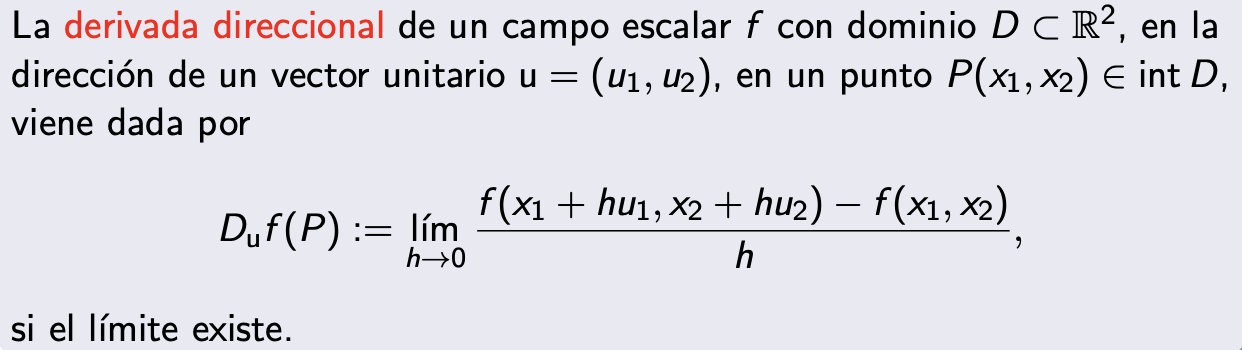
La interpretamos como la tasa de cambio de la función en dirección del vector unitario U en un punto dado. Es un concepto que generaliza la derivada parcial y se utiliza para funciones de varias variables.
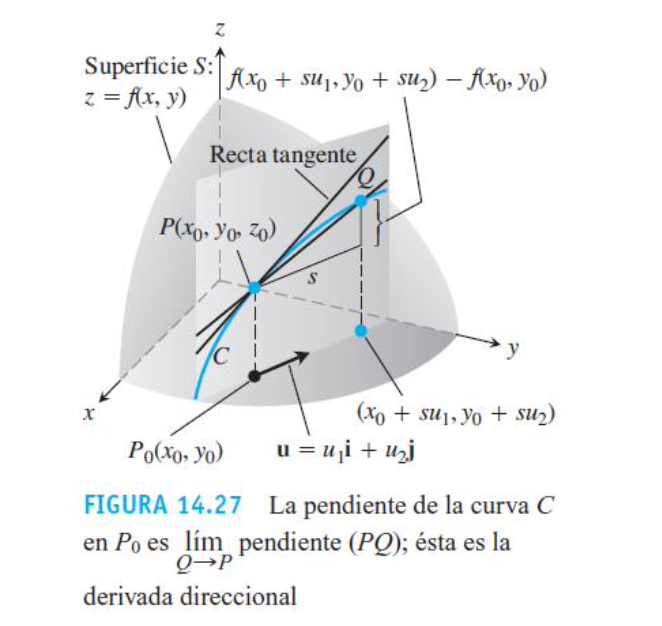
Derivada direccional como producto escalar (demo)

Demostramos usando límite y la regla de la cadena.
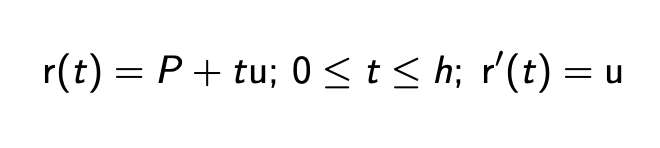
El vector gradiente es normal a la curva de nivel o superficie

Para la demo, partimos de parametrizar una curva de nivel de f, r(t)=(x(t);y(t)); que pasa por un punto P0, r(t0)=P0.
Al ser una curva de nivel, para todo t, f(r(t))=0.
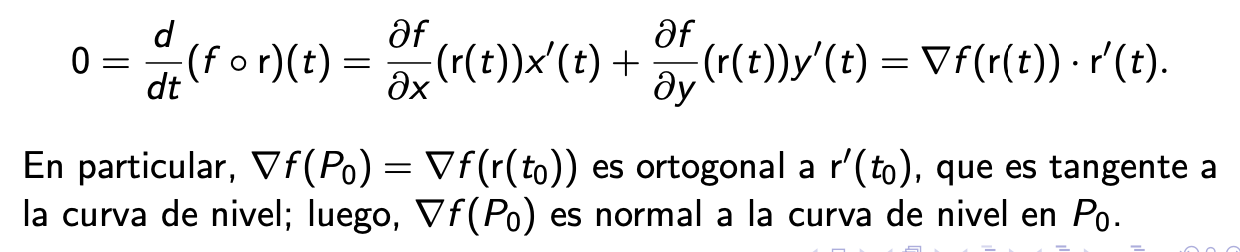
Linealización
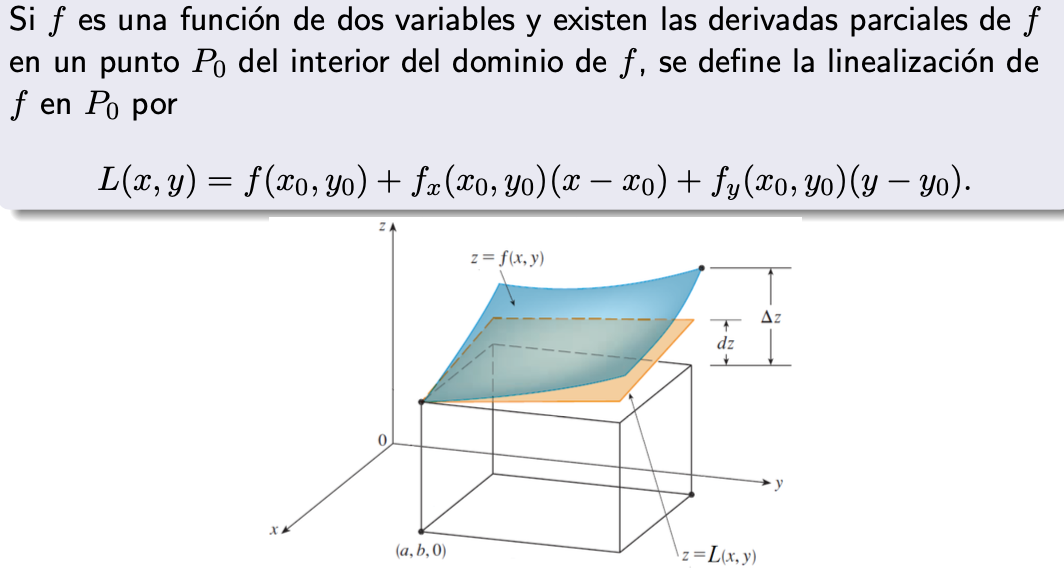
La linealización tiene los mismos términos que ∆f. En el gráfico vemos que ∆z representa la variación de la función de dos variables y dz representa la variación de la función linealización.
Observación: si f es diferenciable en P0, L provee una buena aproximación de f en un entorno de P0.
En el caso de una función de tres variables, se cumplen las mismas hipótesis, sin embargo, no hay representación gráfica.
Máximos y mínimos
Si f está establecida en una zona que incluye al punto (a; b) y f(a; b)≥ f(x,y) para todos los (x,y) ∈ D(f) de alguna f(a,b), se considera que f alcanza un (valor) máximo local en (a, b).
Si f está establecida en una zona que incluye al punto (a; b) y f(a; b)≤ f(x,y) para todos los (x,y) ∈ D(f) de alguna f(a,b), se considera que f alcanza un (valor) mínimo local en (a, b).
Criterio de la derivada primera para extremos locales (demo)
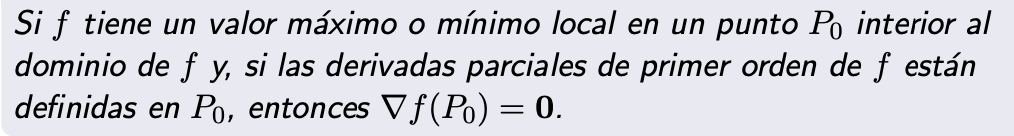
Supongamos que f(x0,y0) es un valor extremo local de f. Entonces la función f(x,y0), como función de una variable independiente, también tiene un extremo en x = x0. Por el criterio de la derivada primera para funciones de una variable, si la derivada existe en x0 debe ser cero. Luego fx(x0, y0) = 0.
Similarmente, se prueba que fy(x0,y0) = 0.
Criterio de la derivada segunda para valores extremos locales (demo)
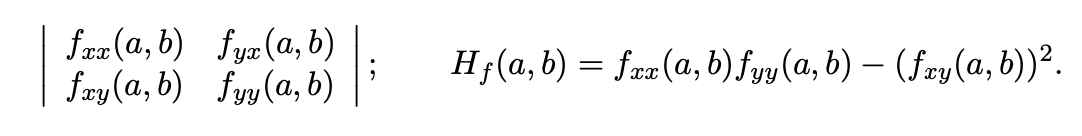

La demo tiene tres partes, partimos de relacionar la función f con su serie de Taylor hasta el orden 2 con centro en (a;b) en una región abierta R. Tomamos un c que pertenece entre 0 y 1. En este caso se cumplen