biostats - unit 3

problem multivariate analysis solves

in biology, many factors simultaneously affect response variable

factorial experimental designs

multiple variables are tested simultaneously and every possible combination of the factors is included

assessing parametric assumptions

use residuals because raw data contains too many groups

poison distribution

data are discrete (no fractions), counting rare (random) events

tweedie distribution

use for data with a lot of zeroes

interaction

effect of one explanatory variable depends on effect of another explanatory variable

two-way ANOVA

have two independent categorical predictor variables and one dependent continuous response variable

two-way ANOVA vs normal ANOVA

two-way: effects of two independent variables on a dependent variable, and also tests for any interaction between the two

normal ANOVA: compares means of three or more groups based on the independent variable (only one independent variable)

hypotheses for interactions

what does an interaction imply

effect of 1 variable on the response depends on the value of the 2nd variable

why we don’t just conduct two t-tests or two regressions separately?

leads to multiple comparisons fallacy

multiple comparisons fallacy

when you run too many statistical tests and forget that each test has it’s own chance of a false positive —> start finding “significant” results by random chance, not cuz they’re real

• essentially, it inflates probability of running into a false positive

why we can’t just include every variable

will lead to overfitting and collinearity

overfitting

model is too complex and memorizes noise from training data instead of learning the true signal

• model will fit current data well but not new data

collinearity

two or more predictors in model are highly correlated, making it hard to estimate the true effect of each separately

• like asking if the sun or the temperature causes ice cream to melt more quickly…

what does emmeans do

reports means for us to compare in a table format

what does Tukey-Kramer test do

helps determine which groups were significantly different from the others (absolutely need to use if we have more than 2 levels of any explanatory variables)

principles of experimental design

replication, randomization, reduction of variance, manipulation vs observation, types of variables, hypotheses

replication

does mean trait value of our sample represent the true mean of our population?

randomization

does every part of our population have equal chances of being in our sample?

does every part of our sample have equal chances of being assigned to any treatment group?

reduction of variance

reduce noise - how can we reduce variation that is not relevant to our research question in our samples?

how can we distribute naturally occurring variation across our treatments?

matched pairs design

helps reduce noise —> match each participant with closest partner —> randomly assign one partner and automatically assign the other to the other group

manipulation vs observation

are we creating the groups or are we making comparisons between naturally occurring groups?

drawback of experimental design

can add structure we don’t want to our data

structure we want to our data

• experimental treatment groups

• naturally-occurring variation we are interested in studying

structure we don’t want in our data

• familial, temporal, or spatial similarity

  • individual-level effects (repeated measurements on same individual)

non-independence

examples = structure we don’t want

means we have committed pseudoreplication

pseudoreplication

researchers mistakenly treat non-independent observations as if they were independent replicates in statistical analysis

• inflates degrees of freedom and sample size

pairing and random effects

accounts for structure we don’t want mathematically

paired t-tests

pair experimental units based on shared information to distribute natural variation across treatments

two-sample design vs paired design

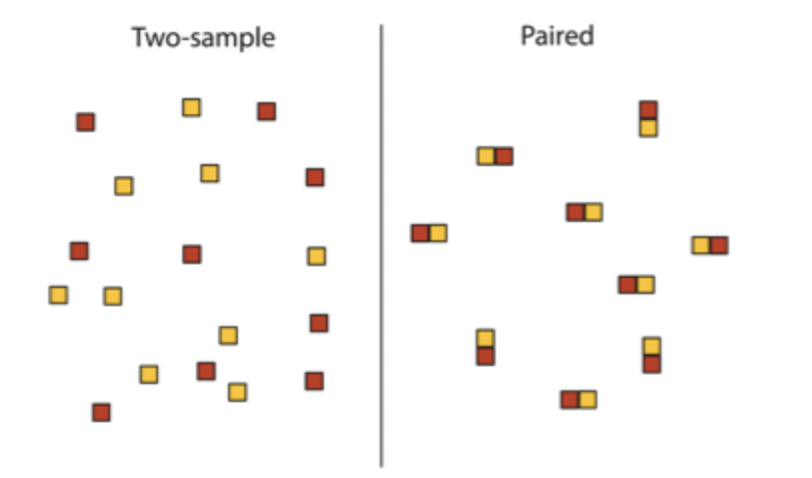
random effects

simplest way to control for unwanted structure in our data in all other tests

fixed effects

predefined, repeatable groups with measurable magnitudes

• treatments chosen by researcher

  • interested in magnitude of differences between groups

random effects

occur when groups are randomly sampled from all possible groups in the population

• treatments are a random sample from all possible treatments

  • interested in amount of variation that can be attributed to this effect: variance components

variance components

tells you how much variation is due to random groups, such as families, subjects, etc.

fixed effects model ANOVA

focuses on which groups are different

random effect model ANOVA

focuses on how much does grouping adding variation?

paired t-test assumption check

normality of differences between the two groups

differences ← (blackbirdData$logAfterImplant - blackbirdData$logBeforeImplant)

shapiro.test(differences)

variation in a mixed model

more generalizable (individual identity >1 data point from particular individual or location >1 data point from a particular location)

how glmer controls random effects

allows each group to have it’s own intercept because of the random effect, but still allows us to check for the overall effect of our variable of interest