WONG

The Handbook of God

How do you find the domain of a rational function aka a fraction?

You make the denominator not equal to 0.

How to find the domain of an even root?

You make the radicand, aka the sqrt, >= 0

How to find the domain of an log?

You make the log’s argument > 0

How to find the domain of an exponential?

You make the base > 0

How to find the base of others?

The domain is (-inf,+inf)

How can you tell if a function is an even function?

You can tell if the graph reflects over the y-axis

HOw to tell if a function is an odd function?

You can tell if the graph reflects about the origin

How to tell if a polynomial function is even function?

You can tell if all the powers are even

How to tell if a polynomial function is odd function?

You can tell if all the powers are odd

What does if it means when f(-x) =f(x)?

Its an even function

What does it mean when f(-x) = -f(x)?

Its an odd function

How to graph of y=|f(x)|?

You flip the portion of the negative y up over the x-axis

How to graph y=f(|x|)?

First you delete the graph of the left, if any, then keep and reflect the right side onto the left side.

What are the common trig function values?

remember this order for sin,
(0,0), (π/6,1/2), (π/4, √2/2)),

(π/3, √3/2), (π/2, 1)

cos is the reverse of that order

tan is the sin y values of cos values (0,0)

(π/6, 1/√3) (π/4, 1) (π/3, √3) (π/2, und)

cotx is the reverse of tan

sec is the reciporical of cos

csc is the reciporical of sin, 0 becomes und

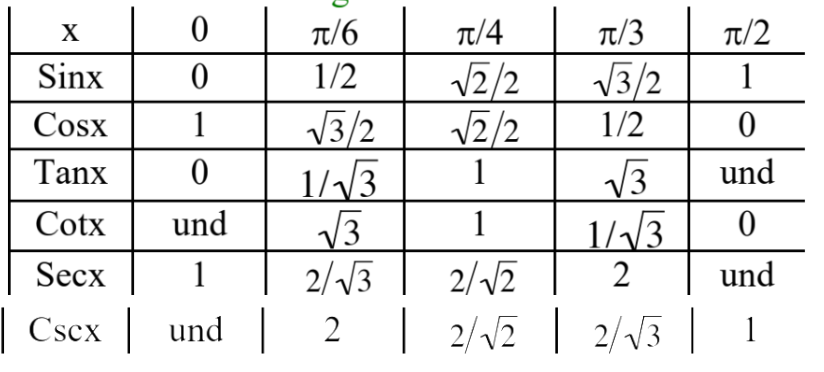
How to use a unit a circle to memorize trig values?

the graphs of sin cos values from the period 2pi divided into 4, and are flipped(1/#) for sec and csc.

Tan x periods are pi divided into 4, being (0,0) (π/4,1) (π/2, und) (3π/4,-1) (π,0) , with cot being flipped

How to get the trig function values if x> pi/2

Use the circle, ASTC, all, sins, tans, and cos(s), from top right going clockwise.

How to solve trig equations?

You have to convert the equation into one of 3 cases, by these formulas,

sin a = sin b
a = b +k2pi, a = pi - b +k2pi

cos a = cos b

a = b + k2pi, a = -b + k2pi

tan a = tan b

a= b + k2pi

Usually, we can ignore k2pi or kpi in calc, for cos, to avoid negative, u can instead add 2pi

How to get the period for sin, cos, sec, csc?

They are all 2pi/a (a being the coefficient of x)

How to get period for tan, cot?

They are all pi/a (a being the coefficient of x)

How to graph a trig function in 1 period?

You make a table, and divide one period into 4 intervals ( 5 numbers), then find the trig values using the trig table. If its und then its a horizontal asymptote.

How to solve an equation with sin or cos involved?

Avoid using the solve command on ti for this, instead put y1=y2 →y1- y2 = 0 and graph it and read the zeros.

To find intersections you can graph both graphs and read the intersections.

How to solve an equation involving absolute values?

Avoid using the solve command on ti for this, instead you should just graph it.

How to find where x →# when given a graph?

If it approaches a number, you check both sides to see if the approach the same location at hole or a point by reading the y

If it approaches at different places then its DNE

How to find where x→inf when given a graph?

If it approaches inf, you check where it levels off, that is your answer,

or if it goes up then its positive infinity, if it goes down then its negative infinity

How to find where x→# when not given a graph?

You plug in the function and simplify, if u get a number, that's your answer,

if you get #/0 it’s DNE, if you get 0/# then it’s 0

If it’s 0/0, you either have to factor and cancel or use L’Hopital’s rule (can be repeated multiple times) to get your answer

How to find where x →inf when not given a graph?

You can use either the end behavior model (EBM), L’Hopital’s rule, or EPL.

EBM you simplify to a number(that's your answer), inf/# which is just inf, #/inf which is just 0

Use L’Hopital’s rule (can be repeated multiple times) when its 0/0

EPL, for only +inf, to simplify big/small into inf, or small/big into 0

What does it mean when a mcq says “must be true”?

It means it’s valid in all cases, and there are no counterexamples that are found.

What does it mean when a mcq says “could be true”?

It’s asking if there is a single example that supports it.

What is the sandwich aka squeeze theorem?

You use it when f(x) is not given explicity and g(x) <= f(x) <= h(x), if the lim of g(x) at a point is the same as the lim of h(x) at the same point, then the lim of f(x) is the same at that point, but if the two limits are not the same, then they are not equal to each other and are DNE. Must be equal to each other

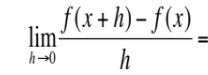
This is equal to what?

f’(x)

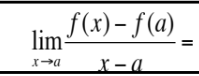
This is equal to what?

f’(a)

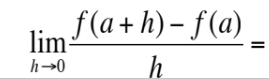
This is equal to what?

f’(a)

How do u find horizontal asymptotes?

EBM, you set it up as the limit of f(x) = L at positive or negative infinity, if the limit is equal to a number, then that’s your Ans, if its pos or neg inf then there is no answer.

How do u find vertical asymptotes?

By the graph you find where the lim of f(x) is pos or neg infinity at x →a- or a+, you can set up to find it by making the denominator of the function = to 0 (its a hole if it can be canceled), or by setting the entire argument of ln to 0

sin or cos has no vert. asymptotes.

How to show a piecewise function to be continuous at the joining point?

You check the if the function value(pluging it in) = left limit = right limit, then it’s continuous, if any steps fail then its discontinuous. By the graph, you check if there is any holes, gaps, or jump at the joining point.

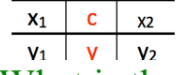
HOw to use IVT?

If f(x) is continuous between x1 and x2 and f(c) is in between y1 and y2, then c is in between x1 and x2.

If c is in between x1 and x2, then f(c) is in between y1 and y2 is wrong, doesn’t apply

Applies to prime when twice differentiable

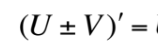
This is equal to what?

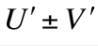
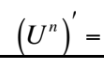
This is equal to what?

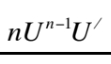
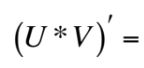
This is equal to what?

U

U’

V

V’

inside 2 + outside 2

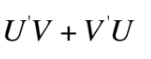
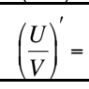
This is equal to what?

U

U’

V

V’

inside 2 + outside 2 all divided by V²

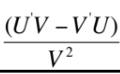
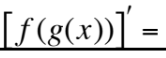
This is equal to what?

outside x inside

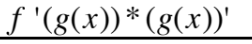
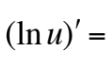
This is equal to what?

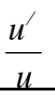
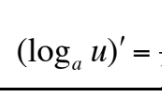
This equal to what?

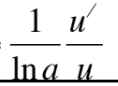
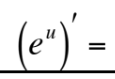
This is equal to what?

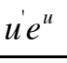
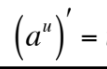
This is equal to what?

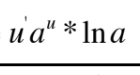
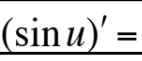
This is equal to what?

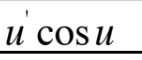
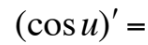
This is equal to what?

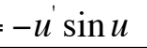
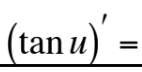
This is equal to what?

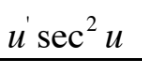
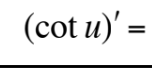
This is equal to what?

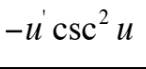
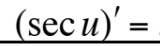
This is equal to what?

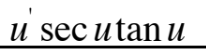
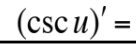
This is equal to what?

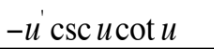
Before find the derivative how should you make the work easier for you?

Simplify the question, by making the product into a sum, quotient into product, and rewrite ln or the exponent.

What are the terms associated with derivatives?

There 12 terms: Instantaneous rate of change, instantaneous rate, rate of change, rate, change, how fast, slope of tangent line, slope of the curve, slope, derivative, differentiation, and prime.

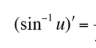
This is equal to what?

put a negative sign in front for inverse cosine

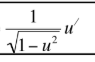
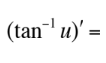
This is equal to what?

put a negative sign in front for inverse cotangent

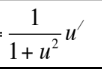
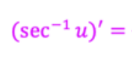
This is equal to what?

put a negative sign in front for inverse cosecant

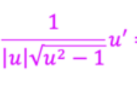
How do u find the derivative of other inverse functions?

given a point of the function f, you find the slope at that point and reciprocate it for the inverse function.

How to find the derivative of a piecewise function?

if the point is within the piece, then use that piece. if its at the joining point, first check for continuity (LL=RV=FV), if so, then find the prime both sides, if they are equal, then that’s your answer.

How to find the derivative of an absolute function?

Given a graph, if its at a linear part, you read the slope by rise over run or MVT for derivative, at the corner its DNE. But if not given a graph, split the absolute value into piecewise, then make the pieces, one pos and one neg, after that set the pos >= 0 and neg < 0, ex. |x-1| = (x-1)>=0 →x>=1, -(x-1) <0 →x<1. then find the prime for which piece the point you are looking for belongs to, joining point is already continuous so just check for the prime of both pieces and plug in.

How to find the derivative of a parametric function?

where the given y function that is primed in respects to t is divided by the x function primed.

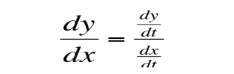
How to find implicit derivative?

U use it when y can’t be isolated, you can do it by finding the prime of both sides then isolating y’

The shortcut to this (only use for mcqs) is where u have to move everything to one side where it is then equal to 0, then y’ = - (derivative of the function respect to x)/(derivative of the function respect to y), when you find the derivative in respect to something then any other variable is treated as a number.

How to estimate the derivative of a point in a table?

You use MVT for the derivative, the function must be differentiable, using the points on both sides if the point is on the table or by using the two points whose interval includes the point we need.

the slope of the tangent line is the same as the slope of the secant line

MVT, logic is that the slope at different points on a straight line are the same

you can use this to find the double prime, given the table values of prime

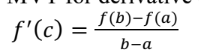
How to read derivative of a point on a line?

You read the slope on rise/run or MVT of the derivative.

How to read derivative of a point of a graph?

You read the slope of the tangent line by rise/run or MVT of the derivative.

How to find the unit of a derivative?

You put y’ = dy/dx where it is equal to the unit of y over the unit of x.

How to interpret a derivative?

Sign, where the rate is increasing when it is + and decreasing when it is -, (be careful when it’s the rate of the rate.

What does differentiablity mean?

diff means y has y’ and y is continuous

twice diff means, it means y has y’ and y is continuous and y has y’’ and y’ is cont.

How to show differentiability?

the graph shows both, show continuity (no hole, gap or jump) and show left derivative = right derivative (no corner, no cusp, no vertical tangent line)

if it is piecewise at the joining point show both, show continuity where FV is equal to LL and RL, and shows left der = right der

any polynomial function is differentiable

How to write the equation of a straight line?

When given (x1,y1) and m = y’ then y-y1 = m(x-x1)

What is a normal line?

It is the line that is perpendicular to the tangent line.

How to convert the tangent line in point-slope form into the normal line at the same point?

Write it as y-y1 = m(x-x1) →y-y1=(1/-m)(x-x1).

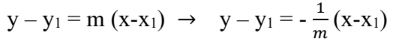
How to make tangent line horizontal or vertical?

Horizontal is when m=0 where in the fraction the numerator is = 0, Vertical is where m=DNE where in the fraction the denominator is = 0.

What is linearization (tangent approximation)?

You approximate the function by using tangent line.

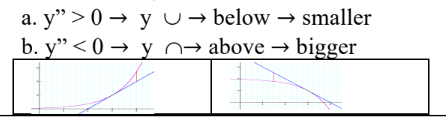
How to compare the tangent approximation with the true value (over or underestimate)?

When y’’ is greater 0 is y concave up is below which means it is smaller, if y’’ is less than 0 is y concave down is above which means it is bigger.

What is a related rates problem?

It is where you are given rates, and you have to find another rate

How to do a related rates problem?

u set up the RR by setting up an equation or using formula, and then derivative both sides with respect to time.

How to set up the equation for related rates?

for angle, you use the trig ratio, for side you use the geometry formulas (Pythagorean theorem, similar angles, volume, area, circumference, perimeter)

How to interpret the sign of rate?

to interpret a sign of a rate, y’+, then y is increasing, and y’ - , then y is decreasing

How to make a sign chart for y= ax +b?

find the signs based on the critical point, opposite sign of a on the left side, sign of a on the right side

if given a graph, do the signs based on the critical point, where below the x-axis is negative, above the x-axis is positive.

When should we extend a sign chart?

extend the sign chart if there are more than one critical point for that one function or extend if there are multiple

What are some exceptions to a sign chart?

even power, a postive number raised to any power (with variable) or absolute value results in only positive values

When can we delete some intervals in the sign chart?

Anything not in the domain, ex. y= sqrt(x), delete everything before the critical point 0

How to make a sign chart in the same name?

How to make a sign chart for the difference of two graphs?

Vice versa applies for the difference of g and f

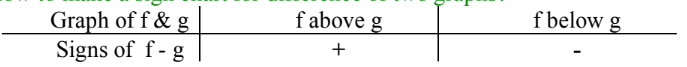
How to make a sign chart for f’ by the graph f?

look at the increasing and decreasing behavior of the graph and make the signs

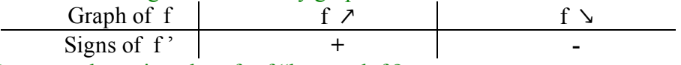
How to make a sign chart for f’’ by the graph of f?

Read the concavity behavior of the graph and determine the signs

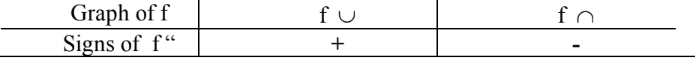
How to make a sign chart for a trinomial function?

same signs outside, opposite signs inside

What is a critical point?

it is where f’ = 0 or undefined and y must be defined at that point,

for a piecewise function that is continuous, check the joining points.

What is a relative (local) max (min)?

It is the highest (lowest) value in a neighborhood

How many ways to find relative/local max or min?

2 ways, 1st derivative test and 2nd derivative test

How to find relative (local), max (min) or inc, dec by first derivative test?

by sign chart, find if it’s increasing or decreasing by checking signs of the prime, then find max or min.

inc to dec is max, dec to inc is min

How to find relative (local), max (min) by second derivative test?

conditions must be y’=0, and it’s a differential equation, make the chart on the point where y’=0, then read the sign of double prime, and see if it’s a max or min based on the concave. Make the prime = 0, find the critical points, from there find the double prime of the function and plug in the critical points u just got to find the signs of the double prime.

How to decide what test to use for relative max or min?

Use the 2nd derivative for a DESF question

What is the Extreme Value Theorem EVT?

Abs max (min) is the highest (lowest) value in the interval, you can apply EVT when the function must be continuous in a closed interval

How many ways can you find absolute max or min?

2 ways, first derivative with end points, and candidate test, requires closed interval for both

HOw to find absolute max or min by candidate test

Find the critical points of the function, the plug those points including the given interval into the y to compare them, smallest # is abs min, biggest # is abs max

How to find absolute max or min by first derivative test with endpoints?

by sign chart, find if it’s increasing or decreasing by checking signs of the prime within the interval, then find max or min.

inc to dec is max, dec to inc is min, then compare the maximum and minimums to find their absolute max or mins.

How to decide what test to use for absolute max or min?

When you can’t make a sign chart use the candidate test.

How many ways to find concavity or point of inflection POI?

There are two ways: the modified sign chart and concavity test

How to find concavity or point of inflection POI by concavity test?

Use concavity test where the chart u look at the 0s/DNE and signs of f’’ to find concavity and POI. POI happens where f’’ changes signs