biom301 mod 4 - probability

probability

you know the population values and predict the likelihood of certain outcomes/samples collected

• opposite of statistics

experiment

the process that yields one random result or observation

• experiment is spinning the spinner

outcome

all the possible results

• outcomes are landing on yellow, green, blue, or red

event

one of the outcomes of interest

• might be interested in landing on blue

probability (spinner example)

the measure of how likely an event is to happen

• the probability of landing on blue is 1 out of 4

  • ¼

  • 25%

  • 0.25

3 probability methods

1. empirically

2. theoretrically

3. subjectively

ways so show probability

• fraction → 10/100

• decimal → 0.1

• percent → 10%

empirical probability

determines probability by running an experiment many times

• used when it’s not obvious what the results should be

• uses results to estimate probability of that even

• long-term behavior (large sample size)

  • P = probability

    • P’ = empirical probability

  • A = specific outcomes

  • n(A) = # of times the event “A” has occurred

  • n = total # of times the experiment is attempted

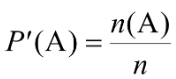
Law of Large Numbers

with repetition, empirical results will approach the expected theoretical probability 

subjective probability

probability determined based on personal judgement

• be critical of a person’s expertise

theoretical probability

calculate probability through reasoning or calculation

• P(A) = theoretical probability

4 approaches to show probability experiment results

1. probability tree

2. sample space

3. venn diagram

4. contingency table

simple events

run the experiment one time

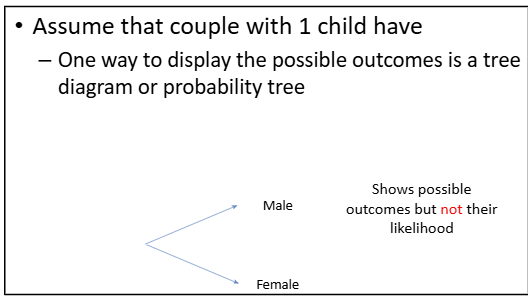
probability tree

shows the outcomes, not probability

sample space

a circle with all possible events inside the circle that are all equally likely

• n(S) = the # of items in the sample space

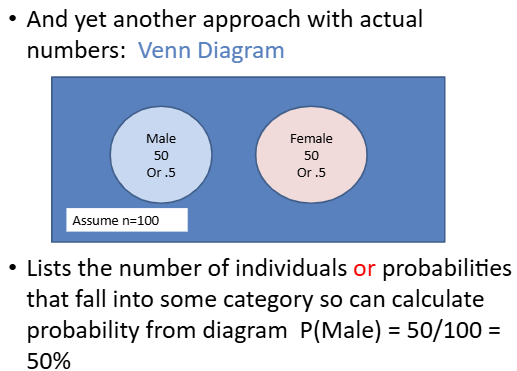
Venn diagram

have circles that each represent an event and inside has the number or percent of the outcomes

• all of the circles = total sample size

contingency table

always gives number of times something happens

• calculate probability from info shown

  • P(female) = 50/100 = 0.5 = 50%

compound events

run the experiment more than 1 times

conditional probability

need to know

• if Event A or Event B occurs

• if Event A and Event B occurs

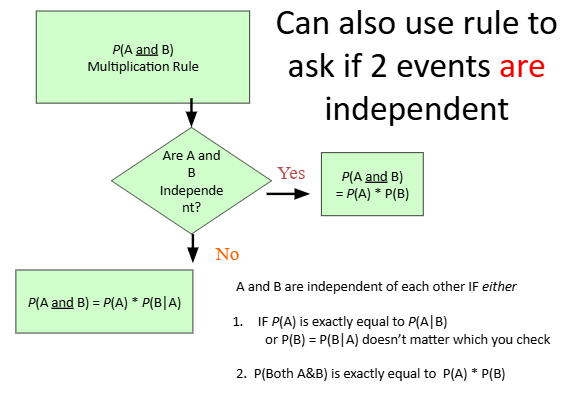
multiplication rule

P(A and B)

• independent events → multiply probabilities together

  • P(2 female children)

    • = P(1st F child) x P(2nd F child) → 0.48 × 0.48 = 0.23 → 23%

  • probability that both will occur will have smaller probability than then individually

  • must be GIVEN probability of both

independence

when the outcome of the 1st event has NO influence on the outcome of the 2nd event

• i.e rolling a dice

  • if 2 events are independent, what is the likelihood that Event A doesn’t change if you are looking at a subset of a population?

addition rule

P(A or B)

• think about whether 1 outcome OR the other occurred

  • mutually exclusive events → ADD probabilities together

• can be done w/ events that are NOT mutually exclusive

  • P(A or B) = P(A) + P(B) - P(both A&B)

    • some outcomes have been double counted & that probability must be removed

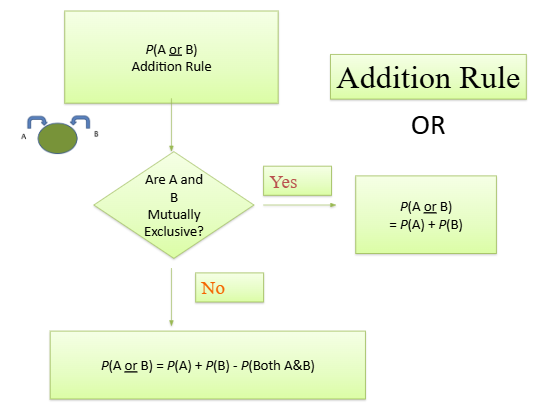
mutually exclusive

dependent events, considering one spot if filled with ‘A’, it can’t be filled with ‘B’

• A & B are mutually exclusive if:

  • P(A&B) = 0

  • P(A or B) = P(A) + P(B)

• more than 1 outcomes fulfill question so probably will increase

  • roll a dice & get ‘6’ OR ‘5’

    • 1/6 + 1/6 = 2/6 → 1/3

compliment

the probability that an event will NOT occur

compliment of A → probability that Event A will NOT occur

• Probability of the compliment = 1

  • P(A) = 1 - P(A)

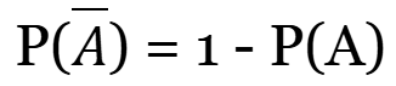
sampling w/o replacements

sample w/o replacement for a compound event, need to change probability of event as you go 

• You have 10 balls in a jar, 7 balls are red, 3 balls are blue.

• What is the probability of randomly sampling WITHOUT REPLACEMENT and getting the following balls in this order:  Red, Red, Blue, Blue?

  • = (7/10) (6/9) (3/8) * (2/7)