Psych 3090 Exam 3 Study Guide

William Gosset

- Irish factory worker at Guinness

- Created the student's t-test

Student's 1 sample t-test

tcalc = (x̄ - μ)/s sub x̄

Logic of 1 sample t test

Population --> Sample --> Experimental treatment --> measure DV --> compare w hypothesized value --> inference (abt a parameter)

alpha

can be .05 or .01 here

Ho

null hypothesis

Ha

alternative hypothesis

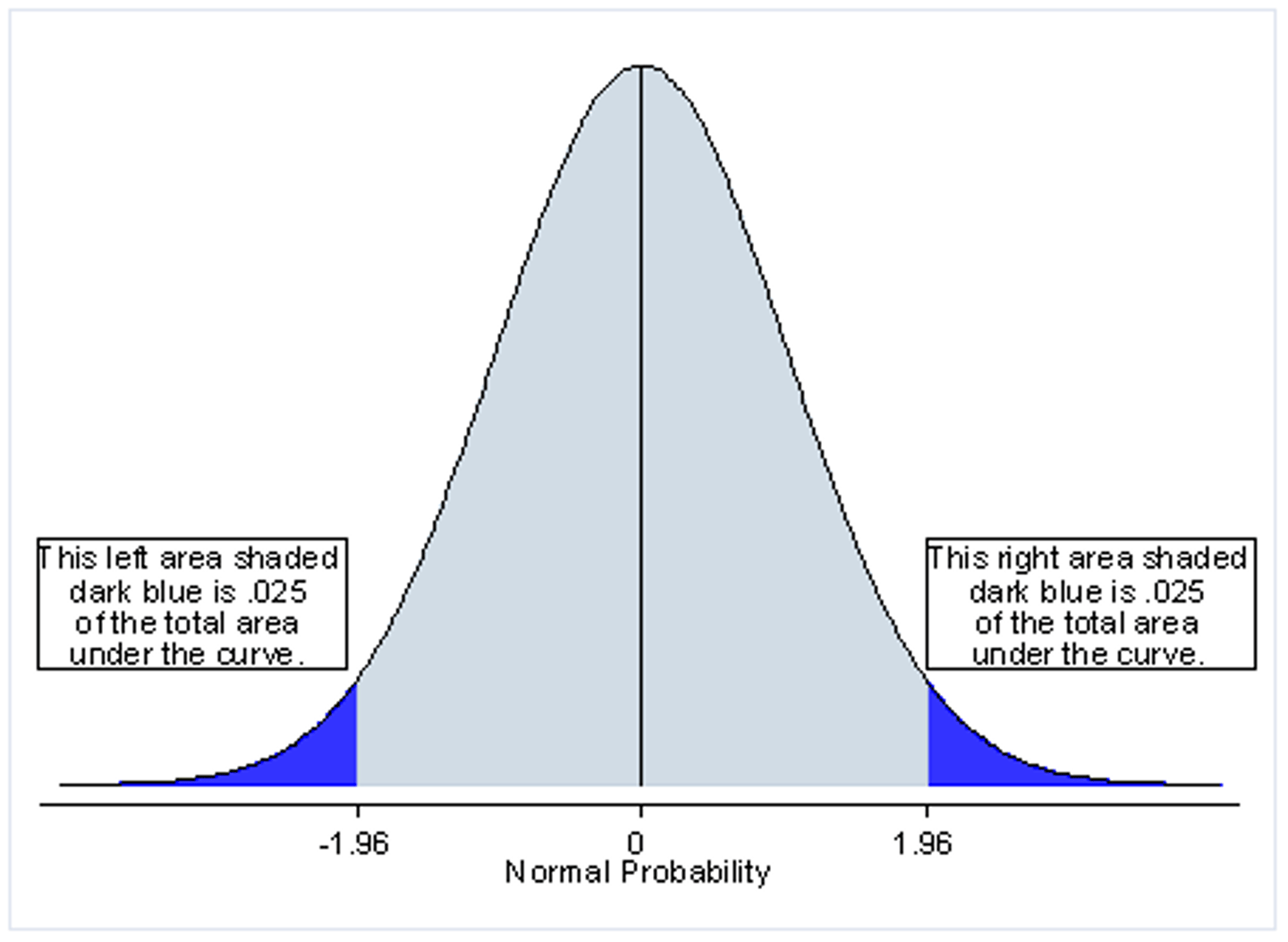
2 tailed t test

- for testing 'non-directional' hypotheses

- ex: "is μ significantly different from...?"

- alpha is split btwn the 2 tails in this t test

- easier to reject Ho with this kind

1 tailed t test

- are for testing 'directional' hypotheses

- ex: "is μ significantly greater than...?"

- Ho: μ < [some value]

- Ha: μ > [some value]

- here alpha is placed entirely in 1 tail

- more powerful but riskier to do

Summary Statement

- All hypothesis tests must end w one

Must Include:

- the DV

- the IV

- the value of both means

- whether the difference was significant

- whether it's a 1 or 2 tailed test

- the value of df

- the value of tcalc

- a p value

p-values

- the prob of getting your result if the null hypothesis were true

- if Ho is rejected then p < α (bc unlikely)

- if fail to reject Ho then p > α (bc likely)

- when reject Ho, " p < .05"

- when fail to reject Ho, "p > .05"

- if exact p value is known, give that instead "p = .03"

Experiments w 2 Conditions

- simplest approach to cause and effect

- the foundation for more complex experiments

- we need tests to compare 2 sample means

between-subjects experiment

- 'independent samples'

- comparing 2 DIFFERENT sample groups

- df = n1 + n2 - 2

within-subjects experiment

- 'dependent samples'

- comparing 2 measurements of SAME sample group

- df = # of pairs - 1

Summary of t tests

- one sample test compares xbar w a hypothesized value

- 2 sample t tests compare 2 xbars

General Pattern:

- tcalc = [(observed value-hypothesized value)/standard error]

One sample t test

- comparing sample against known µ ( unknown σ)

- df = n - 1

Matched sample t test

- special case of within subjects t test

- logic is the same as w/in but instead of measuring each participant twice, measure "matched" pairs of participants

- matched on some relevant characteristic

- use within subjects t test formulas

Steps of "Big picture" logic

1) test an 'omnibus' hypothesis (all means are equal)

2) if Ho is rejected, use "follow up tests" to determine which means are different from which

4 Sources of Variability

1) Individual Differences

2) Measurement error

3) Error in control

4) The Independent variable

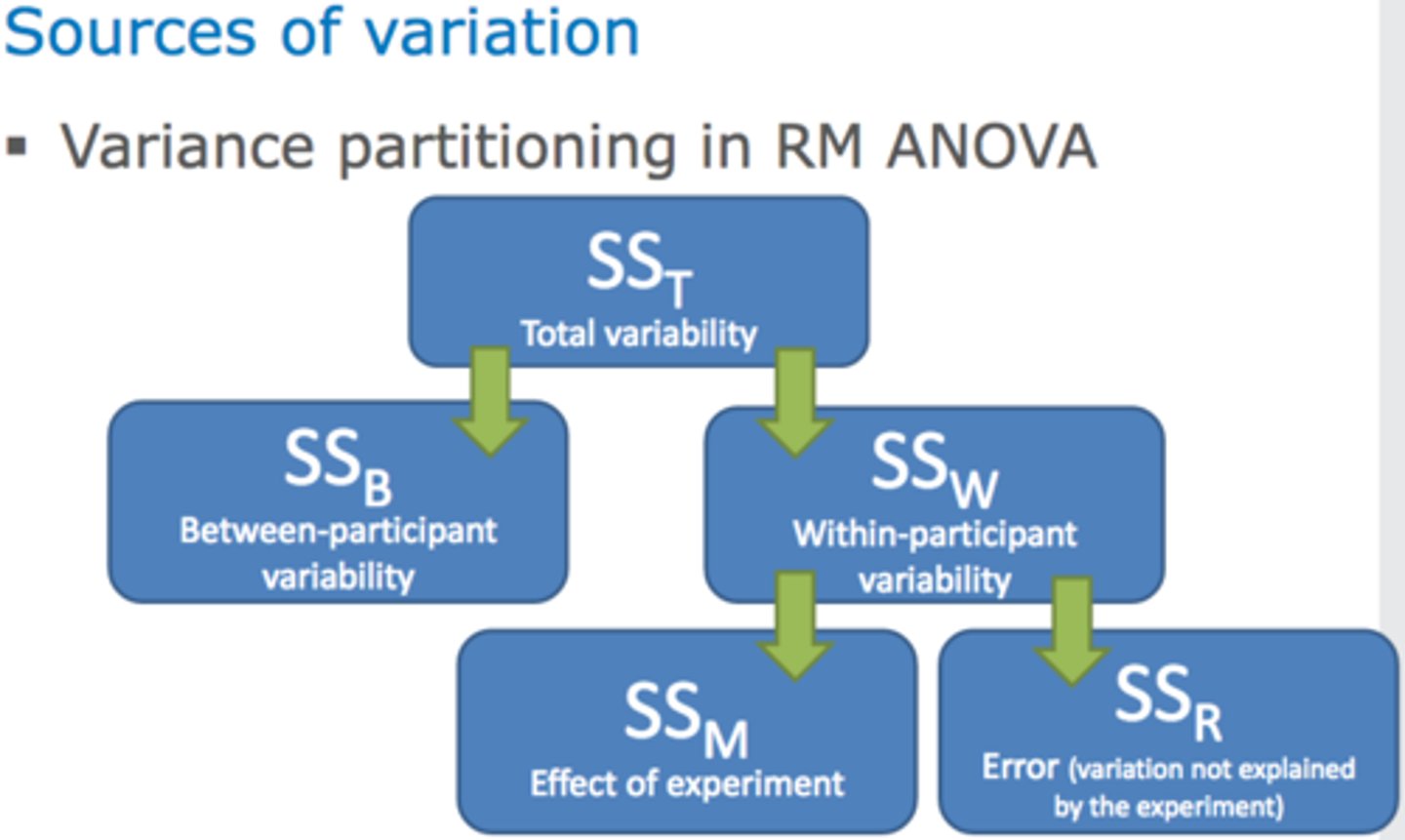
partitioning the variance

Figuring out how much of the total variance is due to the "error" and how much is due to the IV

The critical question in ANOVA

- how big is the variability between conditions (the IV/ MSbtwn) relative to the variability within (error/MSe) conditions?

k

# of conditions (must be 3 or more)

j

refers to any 1 conditions (would be a subscript)

n

sample size of a single condition

N

total sample size (N=nk)

Tj (T subscript j)

sum of scores in condition j

GT

- grand total (sum of Tj -- GT = ΣTj)

- estimates μ (population mean)

GM

- grand mean (GM= GT/nk)

- avg of all data in an experiment

x̅j (x̅ sub j)

- mean of a condition j

- estimates μ subscript j

SStotal

- Σ (x - GM)^2

- this equals SSbtwn + SSwithin

- Deviation: x- GM

SSbetweenconditions

- nΣ(x̅j - GM)^2

- Deviation: x̅j - GM

SSwithinconditions

- Σ(x-x̅j)^2

- Deviation: x-x̅j

df total

- nk-1 = N-1

- = dfbtwn + df within

dfbtwn

k-1

dfwithin

- n-1 for each condition

- k(n-1) = nk - k

The 3 Variances (The 3 Mean Squares)

- MStotal

- MSbtwn

- MSerror

MS(total)

SS total/df total

MS between

SS between/df between

- the good guy

MS error

SS within/df within

- the bad guy

If Fcalc > Fcrit

- reject Ho and conclude that all the population means are not all equal

Why it's Called ANOVA

- if variability between the groups overwhelms the variability within the groups, then we conclude our IV affects our DV

If you reject Ho...

- need to conduct follow up tests to determine which means are different from which

Non-directional

unlikely region is split btwn the 2 tails (2 tailed)

- Ho: μ = 100

- Ha: μ ≠ 100

Directional

unlikely region is entirely in the right tail (1 tailed)

- Ho: μ ≥

- Ha: μ > 100

Why we don't just do multiple t tests...

- Type I error rate gets too high when you do multiple t test --> we'd find a lot of differences that don't exist

Purpose of Follow Up tests

- built to control the type I error rate and prevent it from getting out of control