Modelleren en simuleren vragen H9

Bespreek “Occam's scheermes” ivm modelselectie.

=> Ook bekend als het principe van spaarzaamheid

Occam's scheermes is een principe dat stelt dat, gegeven meerdere verklaringen voor een fenomeen, de eenvoudigste (met de minste aannames of parameters) de voorkeur verdient. In het kader van modelselectie betekent dit dat we eenvoud verkiezen, zolang het model nog goed past bij de data.

Motivatie:

• Esthetiek: eenvoudige theorieën/modellen zijn gemakkelijker uit te leggen en te begrijpen.

• Empirisch: werkt in de praktijk (evolutietheorie, Newtoniaanse mechanica, relativiteit, kwantumfysica).

• Statistisch: minder parameters, dus gemakkelijker te schatten!

Komt op natuurlijke wijze voort uit een Bayesiaans standpunt.

• Modellen met veel parameters krijgen een lagere marginal likelihood, tenzij de extra complexiteit significant bijdraagt aan de verklaring van de data.

Wat betekent het als je model “overfit” op je data en wanneer komt het voor?

Overfitting:

• Het model is te complex en leert niet alleen de echte patronen, maar ook ruis en toevallige details.

• Wanneer komt het voor?

  • Als het model te complex is (bv. veel parameters t.o.v. het aantal observaties).

  • Als er te weinig trainingsdata is.

  • Als er geen goede regularisatie wordt toegepast.

  • Als het model te lang getraind wordt zonder evaluatie op een validatieset.

• Vermijden door:

  • Cross-validatie, regularisatie (zoals L1/L2), en het kiezen van een model met gepaste complexiteit.

Underfitting:

Het model is te simpel en mist belangrijke patronen in de data

Geef 1 voordeel en 2 nadelen van een model complexer te maken

Voordelen:

• Realistischer zijn en specifiekere voorspellingen doen

• Meer gedetailleerde informatie over het systeem weergeven

Nadelen, vergeleken met eenvoudige modellen:

• Vereisen ze meer gegevens om te kalibreren en valideren

• Zijn ze moeilijker te begrijpen

• Zijn ze computationeel kostbaarder

Geef de formule voor de Bayes factor voor modelselectie. Hoe interpreteer je de waarde hiervan?

De Bayes factor wordt gebruikt om twee modellen M1​ en M2​ te vergelijken op basis van hoe goed ze de data verklaren.

Vergelijken van 2 modellen (M₂ vs. M₁) kan gedaan worden via de Bayes factor:

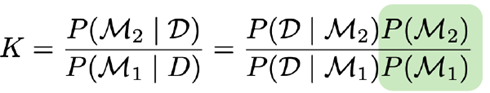
→ De gearceerde term kan geschrapt worden als er geen voorkeur is.

Interpretatie:

• Als K₂₁  > 1 , dan ondersteunt de data model M2​ meer dan model M1.

• Hoe groter K₂₁​, hoe sterker het bewijs voor M2

• Omgekeerd: K₁₂  = 1/K₂₁ ​, dus een klein getal (< 1) wijst in het voordeel van M1.

Jeffreys' schaal (vuistregel voor interpretatie):

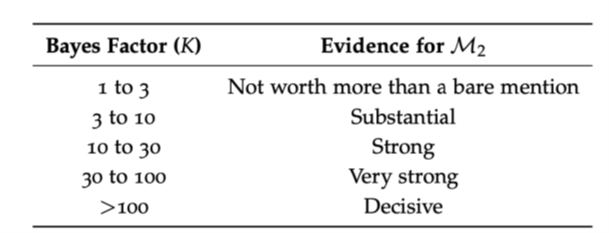
Bespreek hoe de model evidence (P(D|M)) gebruikt kan worden voor Bayesiaanse modelselectie. Waarom is dit moeilijk te schatten?

De model evidence P(D∣M), ook wel marginale likelihood genoemd, is de kans op de data onder een bepaald model M. In Bayesiaanse modelselectie wordt het gebruikt om modellen te vergelijken.

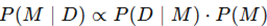
Wanneer we modellen een gelijke prior P(M) geven, bepaalt P(D∣M) direct welke modellen beter worden ondersteund door de data.

• We merken op dat P(D|M), het modelbewijs, de sleutel is voor modelselectie (gemakkelijk om te zetten in P(M|D) met behulp van de regel van Bayes).

• Tot nu toe hebben we er veel moeite voor gedaan om dit niet te berekenen (sampling, MAP…).

  • MAP/MLE geeft alleen de beste waarde van de distributie, niet de spread!

Idee: gebruik samples van een voorwaardelijke keten, samples van P(θ|D,M) en bereken

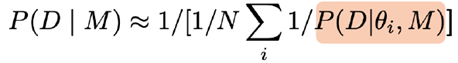
De gearceerde term is de likelihood

Dit wordt de ‘slechtste Monte Carlo-schatter ter wereld’ genoemd

Het berekenen van het modelbewijs kan worden gedaan door de posterior te benaderen, bijvoorbeeld met behulp van de methode van Laplace. We zullen informatiecriteria gebruiken als alternatief.

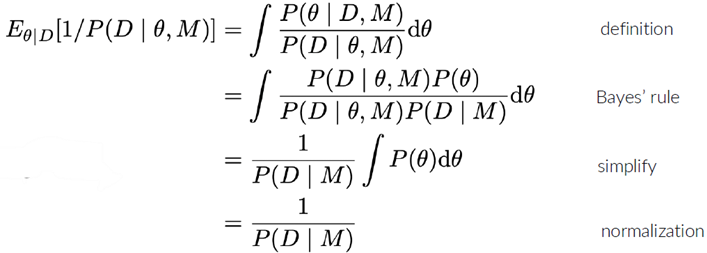
Geef en verklaar de formule voor AIC/BIC en hoe je die kan gebruiken voor modelselectie.

Zowel het Akaike-informatiecriterium (AIC) als het Bayesiaans informatiecriterium (BIC) zijn methodes om modellen te vergelijken op basis van hun fit aan de data én hun complexiteit.

Ze zijn gebaseerd op een benadering van het Bayesiaans modelbewijs en dienen als praktische alternatieven voor volledige Bayesiaanse integratie.

Akaike-informatiecriterium (AIC):

• Formule:

  

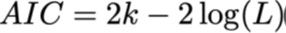
  • L = likelihood van het model gegeven de data

  • k = aantal vrijheidsgraden (parameters, incl. ruis)

  • n = aantal data-observaties

• Verklaring:

  • −2⋅logL meet hoe goed het model de data verklaart (lagere waarde = betere fit).

  • 2k bestraft complexiteit: meer parameters = straf.

• AIC is een praktische metriek voor modelselectie.

• Het brengt fit (waarschijnlijkheid L) en het aantal parameters k (inclusief die voor de ruisverdeling!) in evenwicht.

• Afleiding op basis van de Laplace-benadering.

• Geldig als:

1. Priors vlak/gedomineerd door waarschijnlijkheid zijn

2. Posterieur ongeveer normaal is

3. Steekproefomvang groot is: n >> k

• We kunnen zien dat de AIC gebruikt kan worden voor het berekenen van posterieure modelwaarschijnlijkheid:

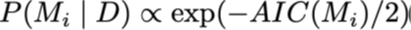
Bayesiaans informatiecriterium (BIC):

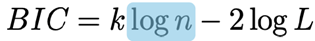
• Is vergelijkbaar, maar verkregen door een andere afleiding en aannames

• Hoe groter je dataset, hoe belangrijker het is om modelcomplexiteit te beperken om overfitting te voorkomen.

• Hier: k*log(n)  bestraft complexiteit: meer parameters = straf.

Reflecties op de informatiecriteria:

• Zowel AIC als BIC zijn niet erg betrouwbaar, maar ze zijn gemakkelijk te berekenen…

• Beter: gebruik het Watanabe-Akaike-informatiecriterium (WAIC)

  • Gebruikt de volledige posterieure keten van parametermonsters

  • Genereert een out-of-sample voorspellende nauwkeurigheid voor elk punt

Gebruik voor modelselectie:

• Vergelijk de AIC- of BIC-waarden van verschillende modellen.

• Lager = beter.

• AIC kiest vaak complexere modellen dan BIC.

• AIC is meer voorspellingsgericht, BIC is meer waarschijnlijkheidsgericht.