BMM Module 11: Molecular Interaction Fields

Cause of interaction of 2 molecules

1. electrostatic effects: + and - attract

2. Hydrophobic effects

   1. Van der Waals

   2. Entropy driven clustering to minimize unfavorable surface contacts with water

Goal MIP

Molecular Interaction Potential

Help us understand how molecules interact with their environment

2 types of MIPs

Molecular Electrostatic Potential (MEP)

• based on true electrostatic fields around a molecule

• shows where molecule are electron rich and electron poor

Molecular Interaction Fields (MIF)

• theoretical tool used to analyze how a molecule is likely to interact with another molecule

• This done by placing a theoretical probe (Hydrophobic, Hb acc or don,…) around a molecule and computing it’s non bonded interaction energies using a force field

• creates a map where probe would experience favorable and unfavorable interactions

• displayed in 3D iso-energy contours

Both methods result in potential fields (energies)

MIP Calculations

Interaction energies of MIP’s are calculated using a grid surrounding the molecule, on each point on the grid a probe is place and the E is calculated

• MEP:

  • Probe = H+

  • Use Coulomb and Poisson Boltzmann equation

• MIF

  • Use molecular probe

  • and non bonded interaction terms from the forcefield

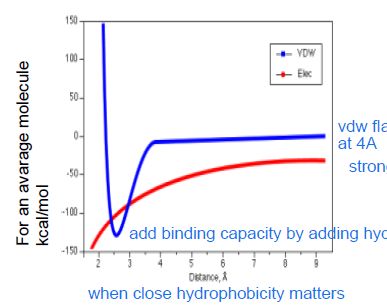
At larger distances:

• electrostatics dominate: important for molecular recognition

At shorter distances (shorter than 3A)

• VDW dominates: to lokck the binder in place

Partial charges of MEP

Describe how electrons are distributed in a molecule and are essential of molecular recognition

Can be estimated by

• Topologica methods

  • define atomtype (EN and structural information of the binding type) and determine values from table

  • Only connectivity required, no 3D geometry

• Quantum chemical methods

  • compute true electorn distributions

  • more accurate but takes longer

MEP defination

= map that shows a positively charged probe (H⁺) would interact with a molecule at different positions in space, describing electrostatic features around the molecule

the countours only show regions where interaction energy is above or below a predefined value

Formula represents:
interaction energy between the probe and particle 2 at gridpoint 1

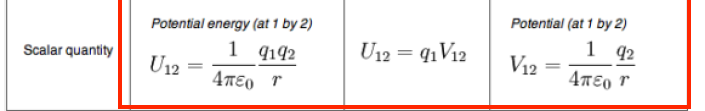
\epsilon

\epsilon = permitivity

• how strongly a medium screens electrostatic interactions compared to vacuum

• higher = charger are screened more strongly

\epsilon r = dielectric constant = relative permitivity

• dimensionless quantity that compares the permitivity to vacuum

• 2~4 in a protein meaning strong electrostatic interactions

Poisson Boltzmann Electrostatics

Coulomb does not account for the continuous changing of solvent properties and electrostatics —> Poisson Boltzmann does: it tells us how the electrostatic potential due to distribution of charges varies in space

\epsilon r\left(r\right) = dielectric constant

\phi\left(r\right) = electrostatic potential
\rho\left(r\right) = charge density

r = position vector

They can all vary with position

Coulomb is just a version of PB where \epsilon is constant (independent of position)

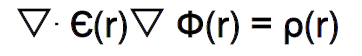
MIFs for molecular recognition

Allow us to see functionalities and properties on a receptor where a ligand can bind using probes

where non bonded terms determine the interection energy (summution of all VDW, electrostatic (and HB) terms)

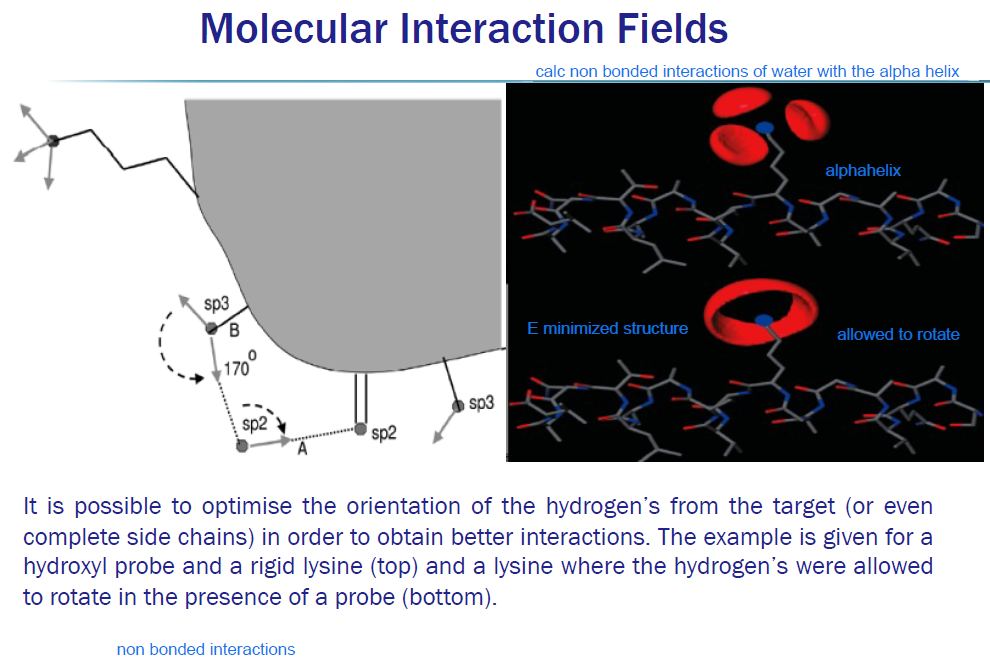
MIFs: Hydrogen orientation

In the top panel:

• Lysine side chain is rigid

• Hydrogen positions are fixed

• Probe orientation is fixed

So only three discrete geometries satisfy:

• correct distance

• correct angle

• no steric clash

Hence → three isolated lobes.

When hydrogens are allowed to rotate:

• Lysine can reorient its H donors

• The system can relax energetically

• More geometries become viable

Result:

• lobes merge or expand

• interaction field becomes smoother and stronger

This is why the bottom panel looks “richer”.

Hydorphobic MIFs

originate from entropy driven clustering of hydrophobic molecules to minimize unfavorable contacts with water

Hydrophobic fields are visualised by using electrostic field to locate the neutral region. At this region, a hydrophibic methyl probe is used to highlight favorable dispersion contacts