Gold Sheets AP Calc

Lim f(x)

x→c

If f(x) is nice (no holes, no asymptotes) let x=c substitute and simplify

if lim f(x) = lim f(x)

    x→c-       x→c+

then lim f(x) exists

          x→c

Finding horizontal asymptotes

End behavior

Find lim f(x)        and lim f(x)

         x→infinity          x→-infinity

Finding vertical asymptotes

Find x-values that you can’t have in the domain (make denominator ONLY = 0)

The limit at that spot from either side = +-infinity

f(x) is continuous at x=a if…

lim f(x)=f(a)

x→a

Intermediate Value Theorem (IVT)

f(x) must take on every value between f(a) and f(b) if f is continuous from x=a to x=b

Average rate of change from a to b

Slope of secant line

f(b) - f(a) / b - a          *old school slope

Instantaneous rate of change at a point x=a

Slope of tangent line at x=a

*use difference quotient

lim f(a+h) - f(a) / h

h→0

Limit definition of a derivative

(Slope at a given point)

lim f(x+h) - f(x) / h

h→0

Alternate definition of a derivative

(at a given point x=a)

lim f(x) - f(a) / x - a

x→a

f(x) is differentiable if…

f(x) is continuous AND lim f(x) = lim f(x)

*slopes match               x→a-      x→a+

d/d(x) (C) =

0 *c is a constant

d/d(x) (xⁿ) =

nx^n-1 *power rule

d/d(x) (c * f(x)) =

c * d/d(x) (f(x))

d/d(x) (u +- v) =

du/dx +- dv/dx

d/d(x) (u * v) =

u * dv/dx + v * du/dx         *Product rule

d/d(x) (u/v) =

(v * du/dx - u * dv/dx) / v²           *Quotient rule

Position =

Velocity =

Acceleration =

s(t)

s^I(t) = v(t)

s^II(t) = v^I(t) = a(t)

Speed

I v(t) I

d/d(x) sinx

cosx

d/d(x) cosx

-sinx

d/d(x) tanx

sec²x

d/d(x) cotx

-csc²x

d/d(x) secx

secxtanx

d/d(x) cscx

-cscxcotx

derivative of a composite function

d/d(x) (f(g(x))) = 

*Chain rule

f^I(g(x)) * g^I(x)

DON’T MESS WITH TEXAS

Slope of parametric equations

(given 2 equations)

x(t) =

y(t) =

dy/dx = (dy/dt) / (dx/dt)

Implicit Differentiation

1. d/dx everything

2. ANY time you have a “y,” tack on a dy/dx to the end

3. Put all dy/dx on same side and solve for dy/dx

d/d(x) (sin^-1(u))

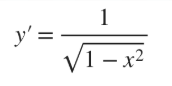
d/d(x) (cos^-1(u))

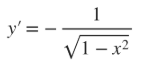
d/d(x) (tan^-1(u))

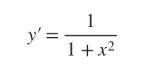
d/d(x) (cot^-1(u))

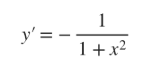
d/d(x) (sec^-1(u))

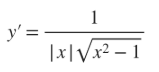
d/d(x) (csc^-1(u))

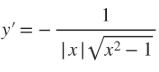
derivatives for inverses let f(x) = g(x) be inverses

*The slopes are reciprocals at inverse points

d/d(x) (e^u) =

e^u * du/dx

d/d(x) (a^u) =

a^u * lna * du/dx

d/d(x) (lnu) =

1/u * du/dx

d/d(x) (log_au) = 

1/(ulna) * du/dx

Extreme Value Theorem

If a function is continuous on a closed interval, the function will have both a maximum and a minimum value in that interval

Critical points (if it is continuous)

Any interior points where f^I(x) = 0 or f^I(x) = undefined

Max or mIn points can occur at:

Endpoints or critical points if f^I(x) changes signs

Mean Value Theorem (MVT) for derivatives

If f is continuous on [a,b] AND differentiable on (a,b) then there exists some value x=c in (a,b) where f^I(C) = (f(b) - f(a)) / b - a

Instantaneous ROC = Average ROC

When finding antiderivatives…

DON’T FORGET +C

Inflection points (if f is continuous)

When concavity changes f^II(x) changes signs