CHEM 2510 / Topic 6b: Liquid Chromatography - Part 2

What is chromatographic resolution R?

How sepped b/w two peaks are.

R=\frac{t_{r,2}-t_{r,1}}{0.5\left(w_2+w_1\right)}=\frac{2\Delta t_{r}}{w_2+w_1}=\frac{0.589\Delta t_{r}}{w_{\frac12\left(avg\right)}}

What does R mean when R is (a) ≈ 0.5, (b) ≈ 1.0, and (3) ≥ 1.5?

• R ≈ 0.5 → heavy overlap.

• R ≈ 1.0 → partial separation.

• R ≥ 1.5 → baseline resolution / cleanly sepped.

What are two ways to improve R?

↑ ∆t_r and ↓ w₁ or w₂ or both

What are two ways to increase R by increasing ∆t_r?

• ↑ solute interac w/ column.

• ↑ column sel for one of the solutes.

What are the three factors of column efficiency?

Capacity factor, column selectivity, and column efficiency.

What does capacity factor k’ measure?

How strongly solute SP-retained.

k^{\prime}=\frac{t_{SP,solute}}{t_{MP,solute}}=\frac{t_{r}-t_{m}}{t_{m}}=\frac{\left(C_{SP}\right)\left(V_{SP}\right)}{\left(C_{MP}\right)\left(V_{MP}\right)}=\frac{t_{r}^{\prime}}{t_{m}}

If solute spends all of its time in MP → elute at t_m.

What does a k’ mean when it is (a) ≈ 0, (b) ≈ 2–10, and (c) > 10?

• low k’ ≈ 0 → small ret, poor sep. (bad).

• high k’ ≈ 2–10 → suff ret for sep, manageable broadening (good).

• very high k’ > 10 → big ret, more band broadening. (bad).

How is the t a solute spends in the SP related to its dist b/w phases?

> t spent in SP ∝ amt in SP
> ↑ SP residence time ↑ fraction of solute in SP
> At eq, solute dist reflects relative phase residence times.

What does the quotient C_SP/C_MP represent?

partition coefficient K

What does column selectivity α measure?

rel sel of column X pair

a=\frac{k^{\prime}_{A}}{k_{B}^{\prime}}

Selectivity factor α is then the ratio of the capacity factor for two solutes. If α = 1, then both solutes have identical elution times.

How can a picture of a width of a band on a column relate to a peak width on a chrom?

> Inside the column, solute exists as band spread over distance.

> Different parts of the band move at slightly different speeds due to interaction w/ SP.

> When front of band exits → detector S starts rising.

> When centre exits → peak max.

> When tail exits → S returns to baseline.

> Flow rate is constant.

> Distance along column ↔ time at detector.

> Wider band in space → longer arrival time window → wider peak.

How does the theoretical plate model explain why increasing the number of plates improves column efficiency?

> column = many tiny eq, partitioning zones = theoretical plates

> ↑ zones ↑ chances to equilibrate → restore the equilibrium MP/SP residence-time distribution, preventing accumulation of velocity dispersion

> Band stays compact → peak stays narrow.

How is the number of theoretical plates N mathematically related to column efficiency?

> N = L / H (where L = length of the column, H = height of each plate)

> Smaller plate height (H) → more plates → narrower peaks → better resolution.

How is the number of theoretical plates N related to peak width?

> N = 16(t_r / w)²

> More theoretical plates → narrower peaks → better efficiency and resolution.

Effectively, if you were to collect capacity factor (talks about retention), column selectivity (talks about separation factor), and column efficiency in one equation, what would it be?

R=\frac14\sqrt{N}\left(\frac{a-1}{a}\right)\left(\frac{k}{1-k}\right)

What are three ways to increase R by fixing w?

• ↑ column length (column eff).

• Regarding selectivity, changing SP can lead to an increase in R (GC), as well as changing composition of MP (LC).

• ↑ k’ ↑ R ← ensures solute spends more time on SP (capacity factor).

What is peak capacity n_c?

max # of solutes theoretically resolved on column → estimate # of solutes feasible to separate.

n_{c}=1+\frac{\sqrt[\placeholder{}]{N}}{4}\ln\frac{V_{\max}}{V_{\min}} where V_max = V_r of first peak and last peak, respectively.

In the van Deemter, what’s happening with the A term?

> packed column = many different flow paths

> Solute particles take different path lengths.

> Some arrive sooner, some later.

Happens regardless of flow rate but happens less with smaller, more uniform particles → less variation in path length.

In the van Deemter, what’s happening with the B/u_x term?

> Solute diffuses fwd & bwd along column axis due to random thermal motion and conc gradient if present.

> The slower the flow, the longer a solute band stays in one place → molecules have to wander randomly → wider distribution.

More time on column, more diffusion = fwd & bwd spread. Faster flow = B/u_x goes down.)

In the van Deemter, what’s happening with the C•u_x term?

> Solute needs time to equilibrate MP ↔ SP.

> The faster the flow, MP moves on before solute finishes exchanging → some molecules lag in SP, others race ahead in MP.

Dominates at high flow. Worse when equil is slow.

When is plate height H minimized in van Deemter?

• To minimize A, use smaller, more uniform packing particles.

• To minimize B/uₓ, increase flow rate to reduce time for longitudinal diffusion.

• To minimize C·uₓ, avoid excessive flow rates and use conditions that allow rapid MP↔SP mass transfer, i.e. when B/u_x = C•u_x

Which van Deemter terms exist in packed columns?

• A ≠ 0 → multiple paths
• B ≠ 0 → longitudinal diffusion
• C ≠ 0 → mass transfer

Which van Deemter terms exist in open tubular columns?

• A = 0 → no packing → no multiple paths.

• B, C ≠ 0 → diffusion & mass transfer still happen.

Which van Deemter terms exist in capillary electrophoresis?

• A = 0 → no packing

• B ≠ 0 → diffusion-limited

• C = 0 → no MP/SP mass transfer

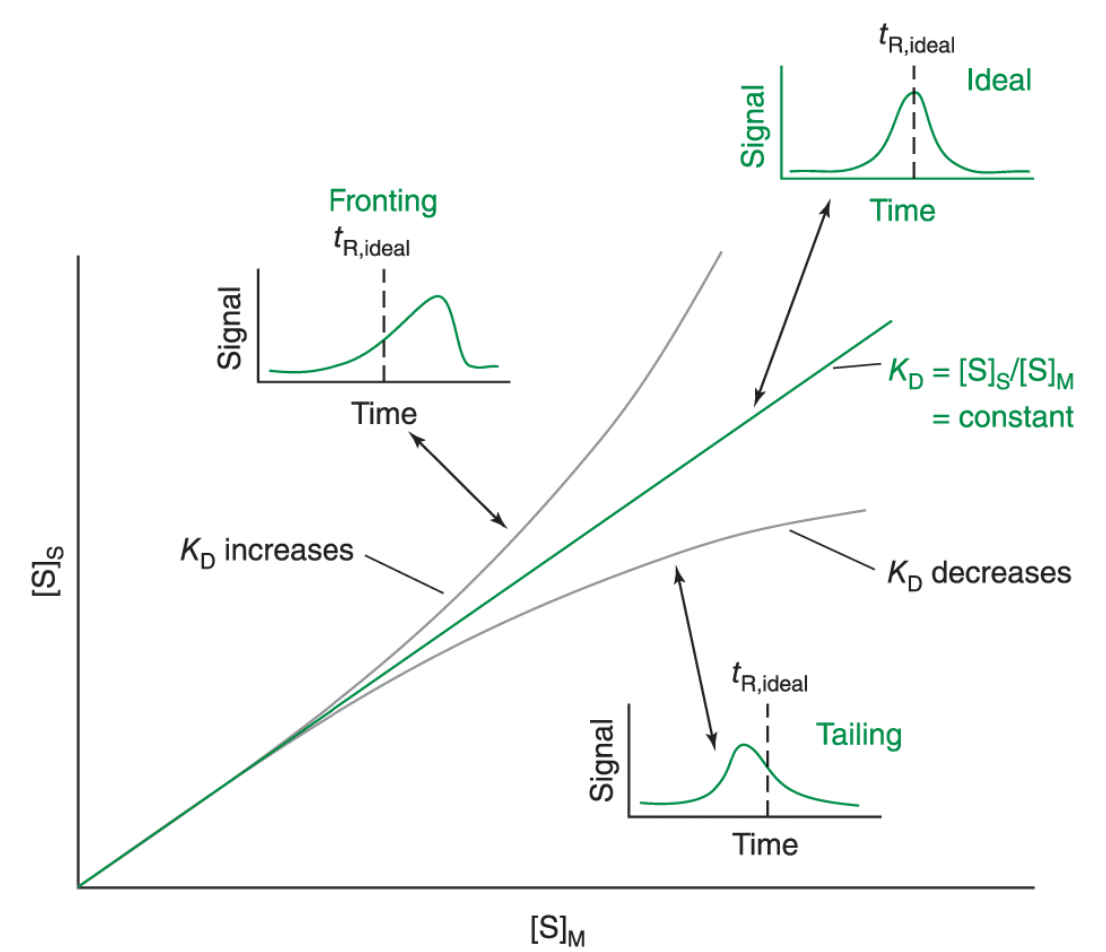
• What is ideal solute behaviour in chromatography?

• What causes non-ideal behaviour?

• What is peak fronting?

• What is peak tailing?

• Ideal: K_D constant at all solute concs → Symmetric (Gaussian) peak.

• Non-ideal: K_D varies w/ solute conc → asymmetric peaks.

• Fronting: Column overloading (SP capacity exceeded) / too much spl injected → ↓ K_D at high solute conc → asymmetry at front of peak.

• Tailing: Active/heterogenous sites on SP → Some solute bind/retained longer than rest → ↑ K_D at high solute conc → asymmetry at end of peak.