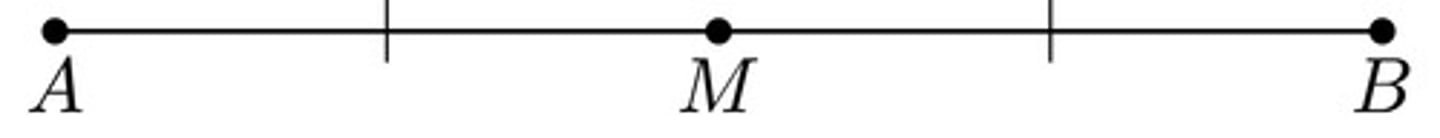Unit 1: Deductive Reasoning and Basic Figures (Geometry 9)

Point

A location with no shape or size; 0 dimensional.

Named by using a capital letter.

Ex: point A

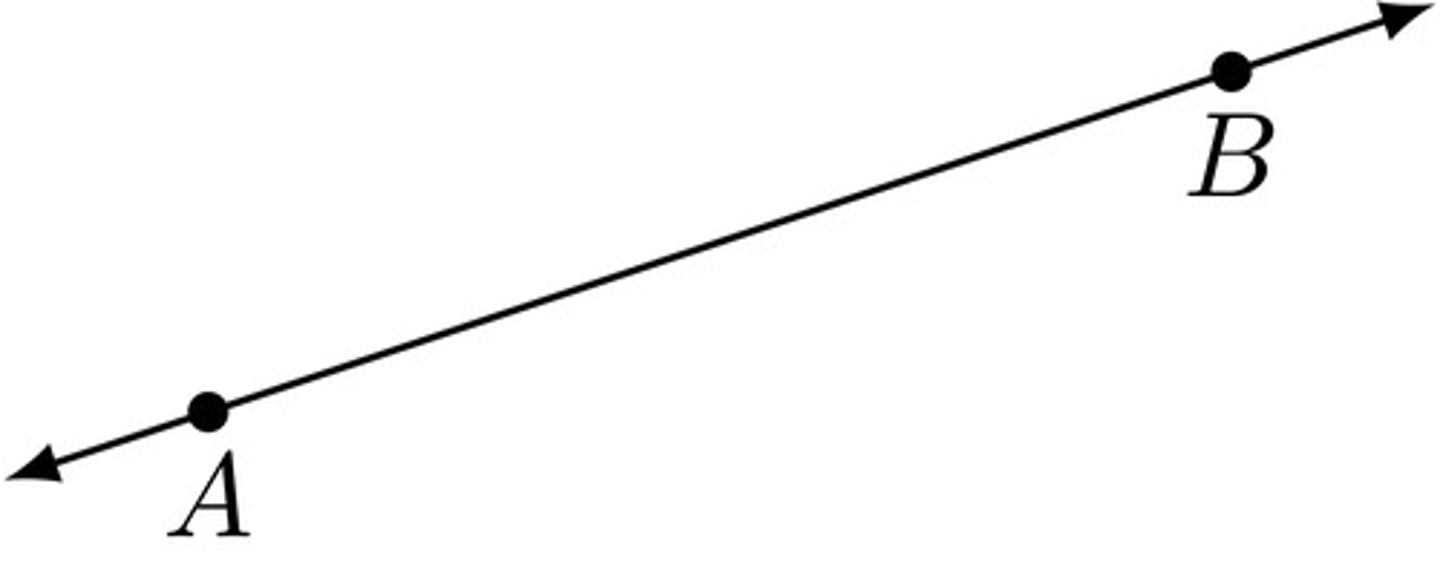
Line

A set of infinitely many points that extends in 2 directions; 1 dimensional (has no thickness or width).

Named by using any 2 points.

Ex: line AB (or line BA)

Plane

A flat surface that is the set of infinitely many points and extends in all directions; 2 dimensional has no thickness.

Named by using any 3 noncollinear points.

Ex: plane ABC (or plane BCA, etc.)

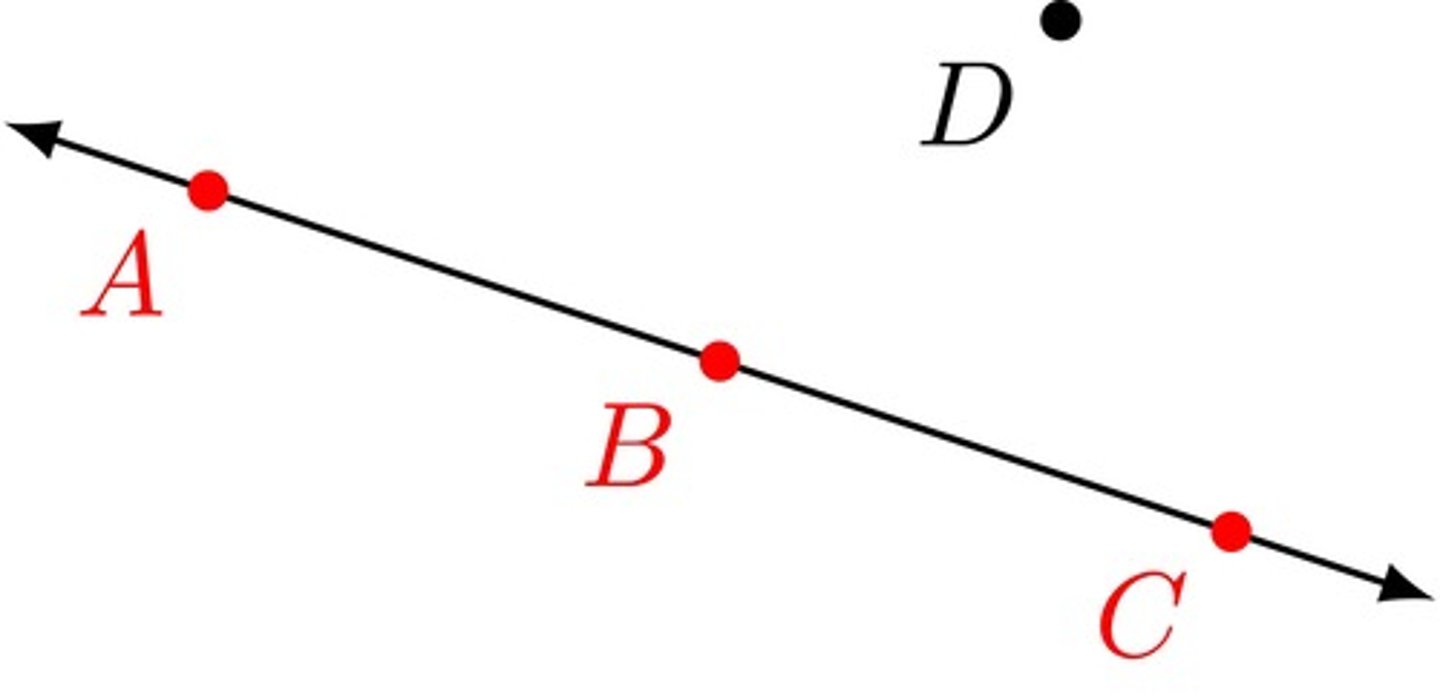
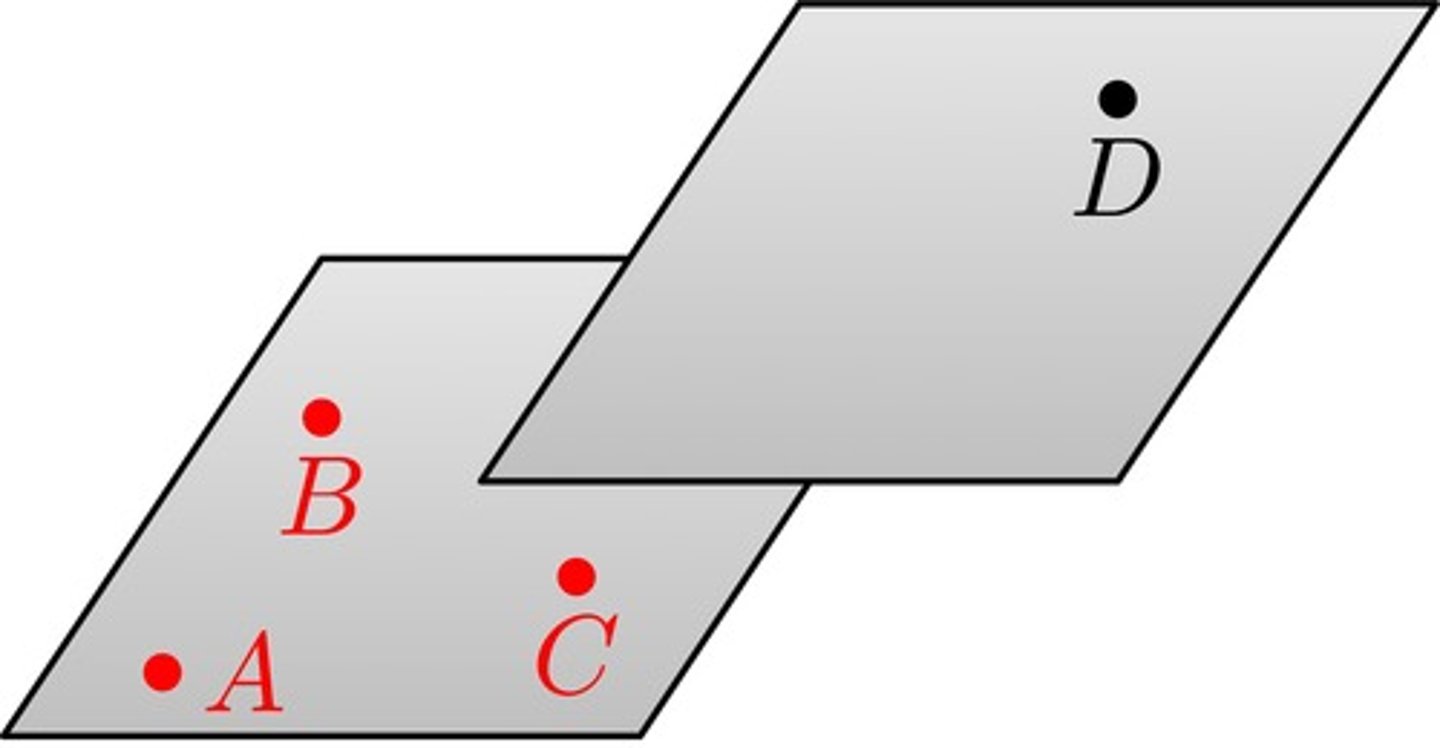
Collinear Points

Points that lie on the same line.

Ex: A, B, and C are collinear. A, B, and D are noncollinear.

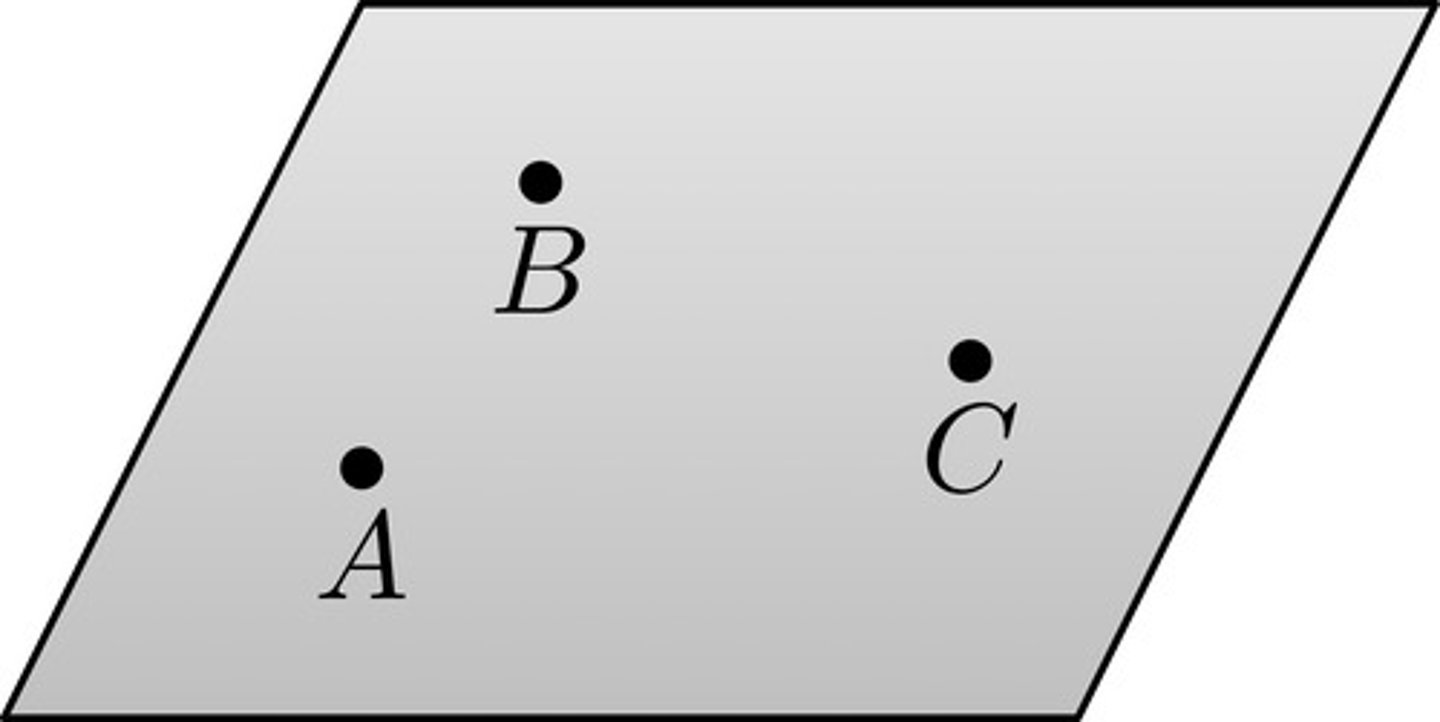
Coplanar Points

Points that lie on the same plane.

Ex: A, B, and C are coplanar. A, B, C, and D are noncoplanar.

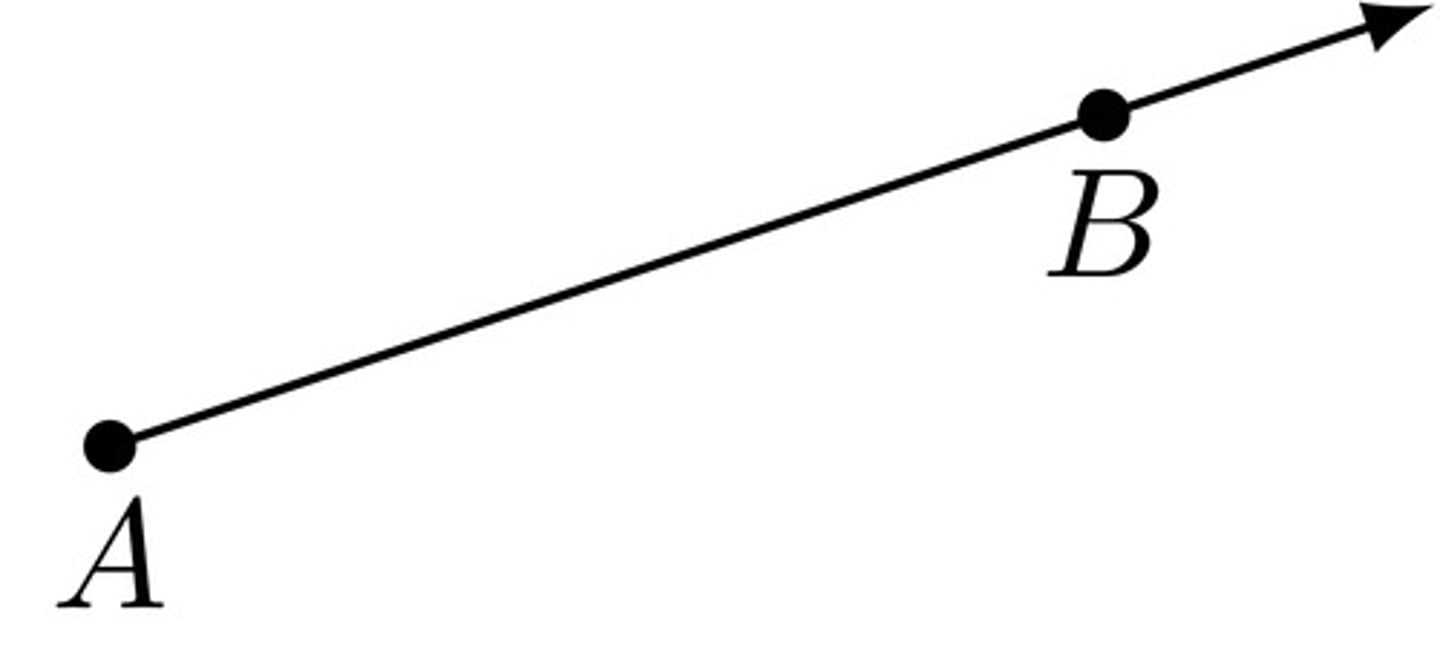
Ray

A part of a line that extends infinitely in 1 direction; has 1 endpoint.

Named with its endpoint first.

Ex: ray AB (NOT ray BA)

Opposite Rays

Rays that share an endpoint and form a line.

Ex: ray BA and ray BC are opposite rays

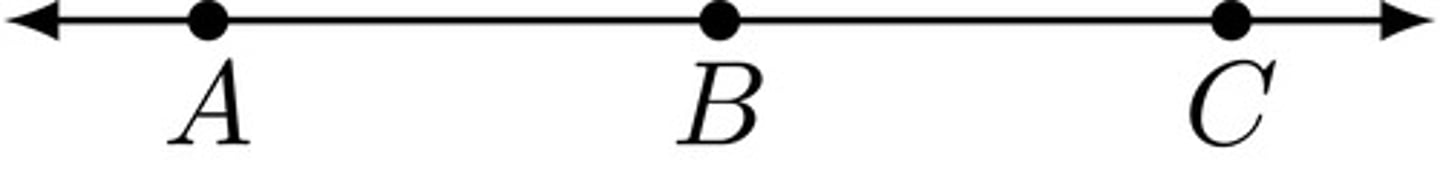
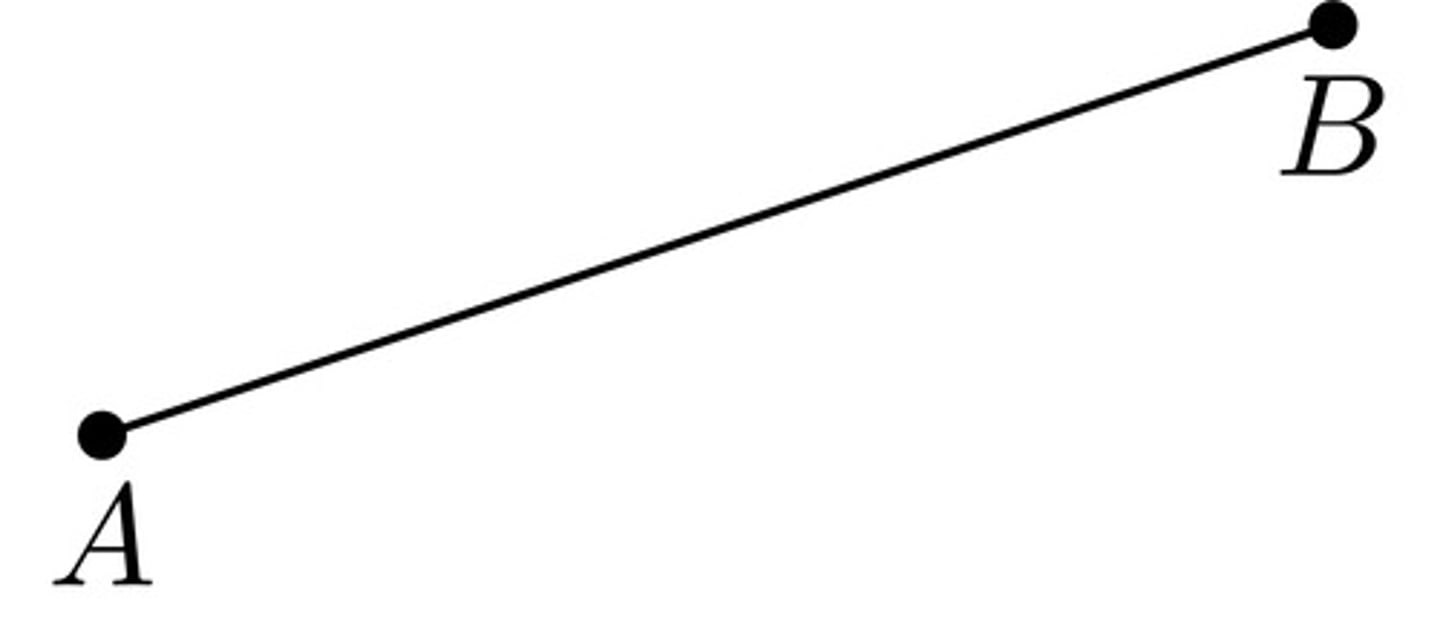
Line Segment

A measurable part of a line; consists of 2 endpoints and all points in between.

Named by using its endpoints.

Ex: segment AB (or segment BA)

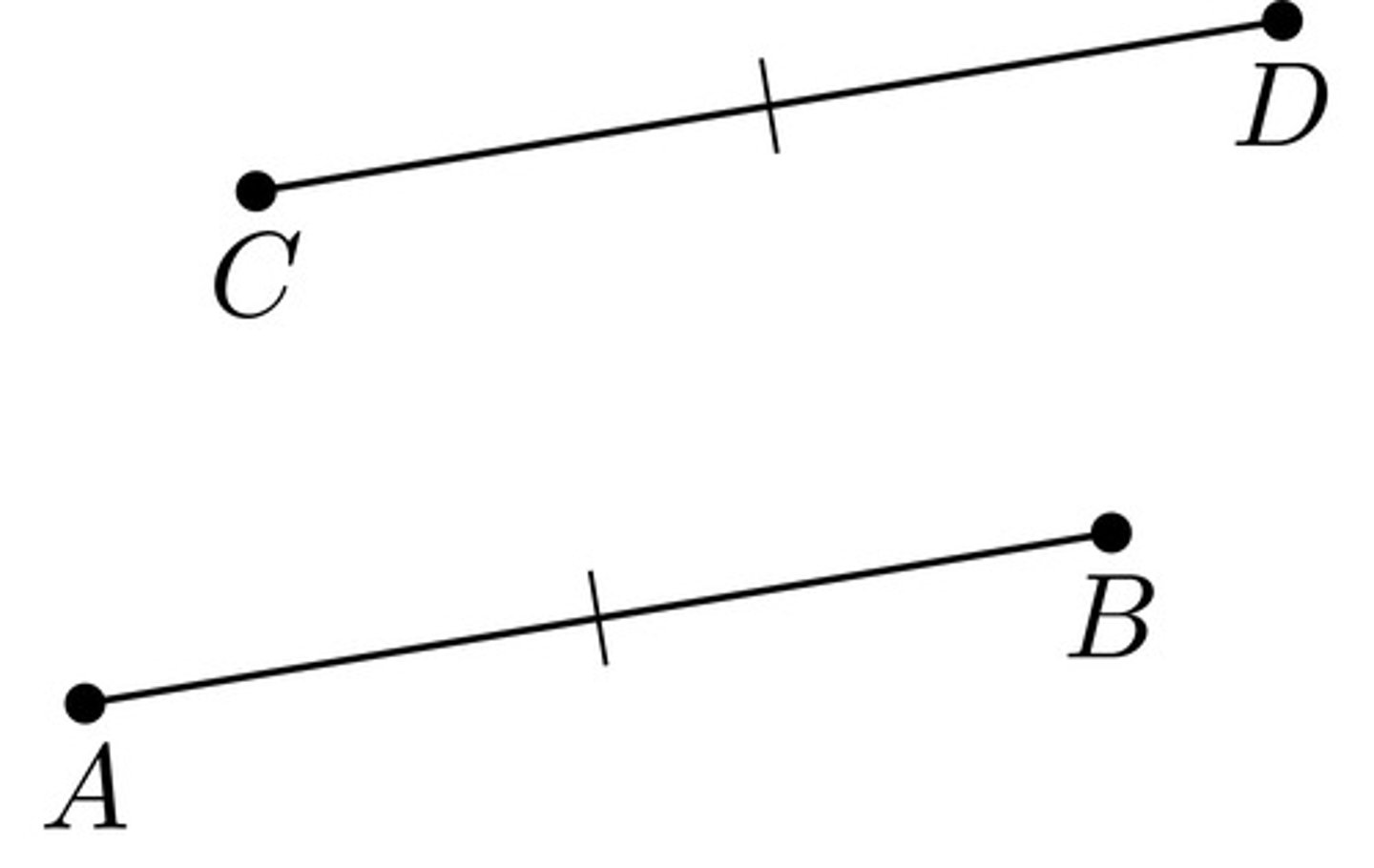
Congruent Segments

Line segments that have the same length.

Ex: segment AB ≅ segment CD

Midpoint

A point on a segment that divides the segment into 2 congruent segments.

Ex: M is the midpoint of segment AB

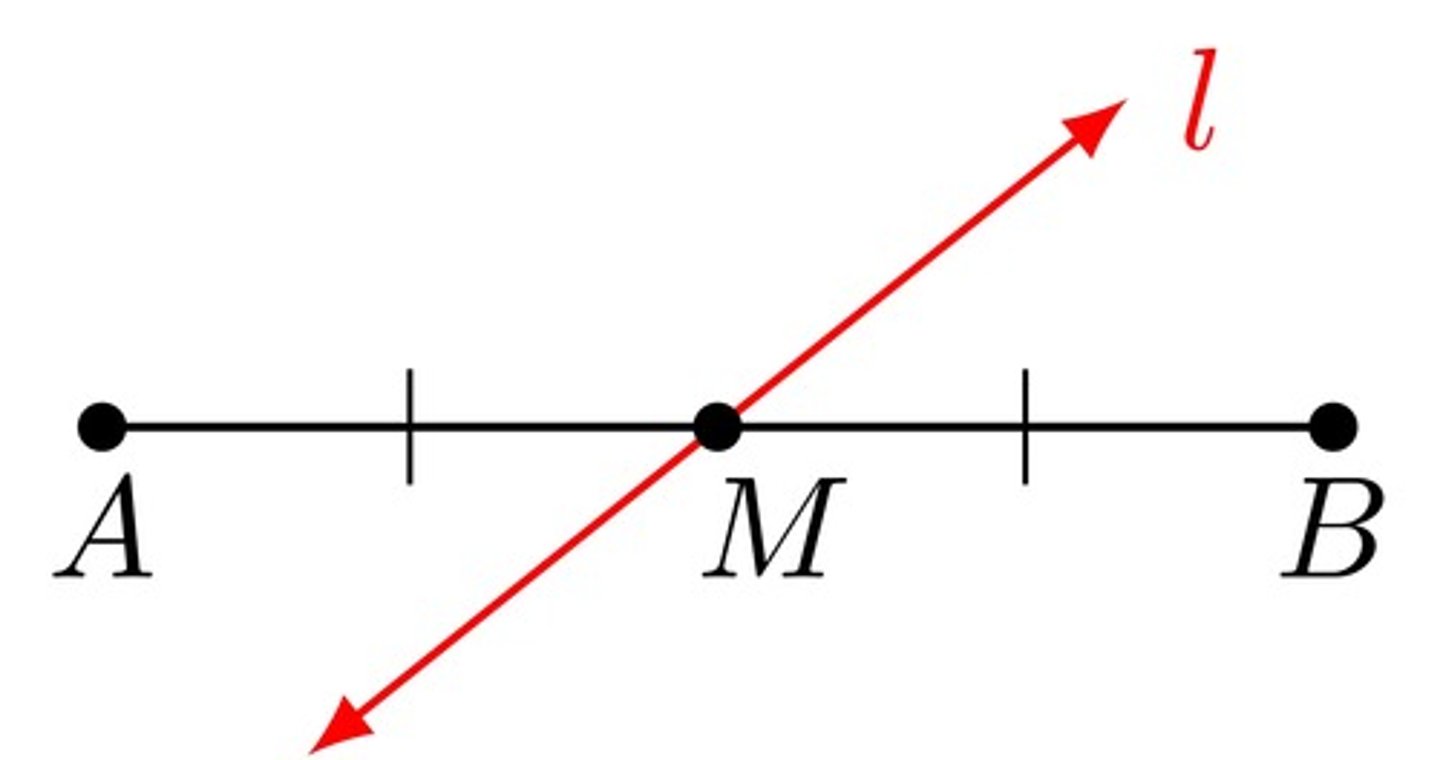
Segment Bisector

A line, ray, segment, or plane that intersects a segment at its midpoint.

Ex: line l bisects segment AB

Proposition

A statement that has exactly 1 truth value (true or false).

Conditional Statement

A statement whose basic form is the proposition "if P, then Q" (denoted P → Q).

P is the hypothesis.

Q is the conclusion.

Converse of P → Q

Q → P

Biconditional Statement

The proposition that "P if and only if Q," also written as "P iff Q" (denoted P ↔ Q).

All definitions can be written as biconditional statements.

Counterexample

An example that proves a statement false.

Reflexive Property of Equality

a = a

Transitive Property of Equality

If a = b and b = c, then a = c.

Substitution

If a = b, then either a or b may be substituted for the other in any equation or inequality.

Addition Property of Equality

If a = b, then a + c = b + c.

Subtraction Property of Equality

If a = b, then a - c = b - c.

Multiplication Property of Equality

If a = b and c ≠ 0, then ac = bc.

Division Property of Equality

If a = b and c ≠ 0, then a ÷ c = b ÷ c.

Reflexive Property of Congruence

∠A ≅ ∠A

This applies to all figures that can be congruent (segments, angles, polygons, circles, etc.).

Transitive Property of Congruence

If ∠A ≅ ∠B and ∠B ≅ ∠C, then ∠A ≅ ∠C.

This applies to all figures that can be congruent (segments, angles, polygons, circles, etc.).

Postulate

A statement that is accepted without proof.

Theorem

A statement that can be proven.

A line contains at least ___ points.

A line contains at least 2 points.

A plane contains at least ___ points not all in ___ line.

A plane contains at least 3 points not all in 1 line.

Space contains at least ___ points not all in ___ plane.

Space contains at least 4 points not all in 1 plane.

Through any 2 points there is exactly ___ line.

Through any 2 points there is exactly 1 line.

If 2 lines intersect, then they intersect at exactly ___ point.

If 2 lines intersect, then they intersect at exactly 1 point.

Through any 3 points there is ______ 1 plane, and through any 3 noncollinear points there is ______ 1 plane.

Through any 3 points there is at least 1 plane, and through any 3 noncollinear points there is exactly 1 plane.

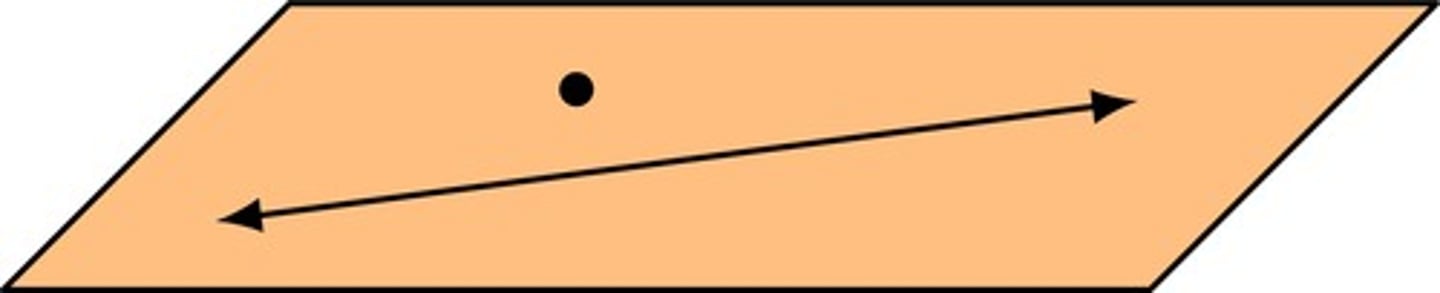
Through a line and a point not in the line there is exactly ___ plane.

Through a line and a point not in the line there is exactly 1 plane.

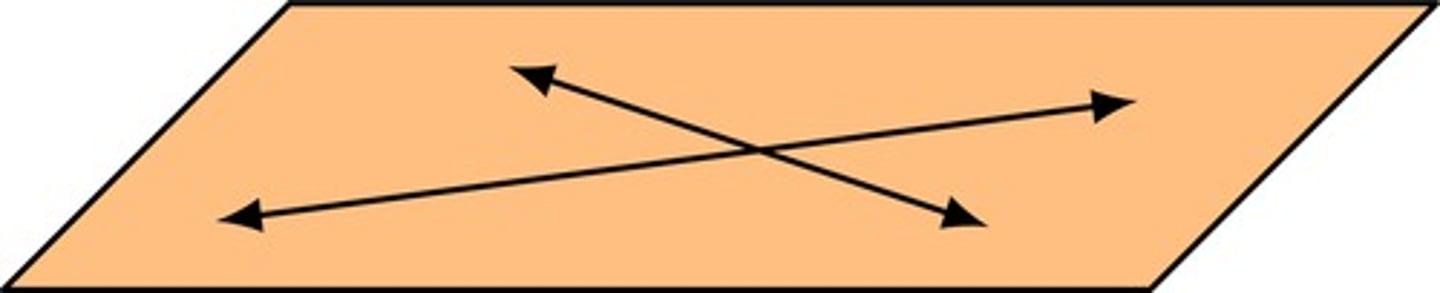
If 2 lines intersect, then exactly ___ plane contains the lines.

If 2 lines intersect, then exactly 1 plane contains the lines.

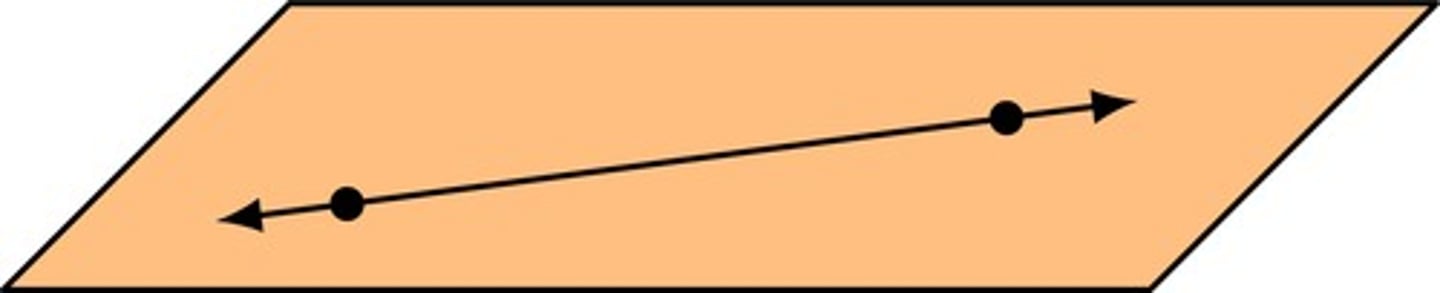
If 2 points are in a plane, then the line that contains the points is...

If 2 points are in a plane, then the line that contains the points is in the same plane.

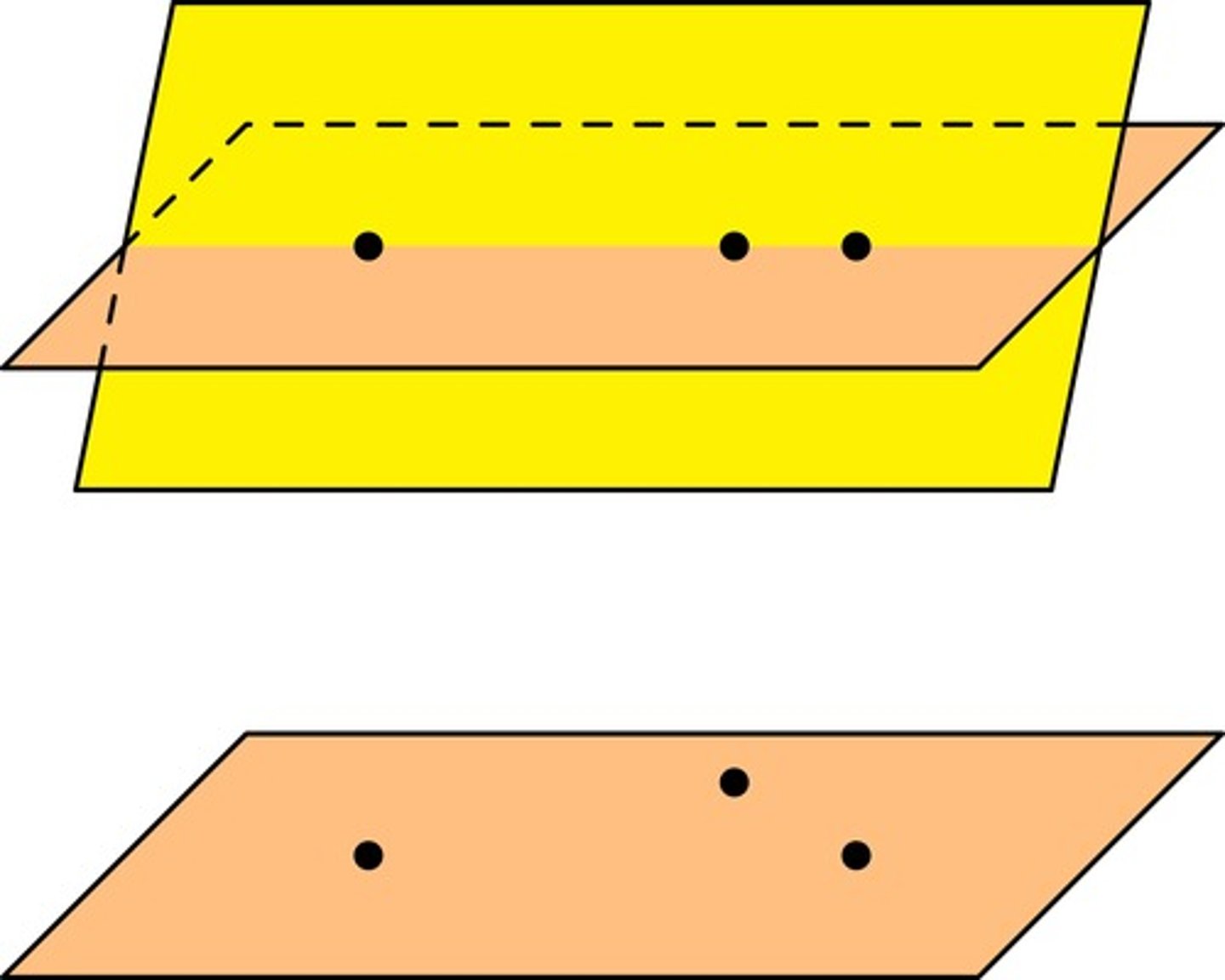
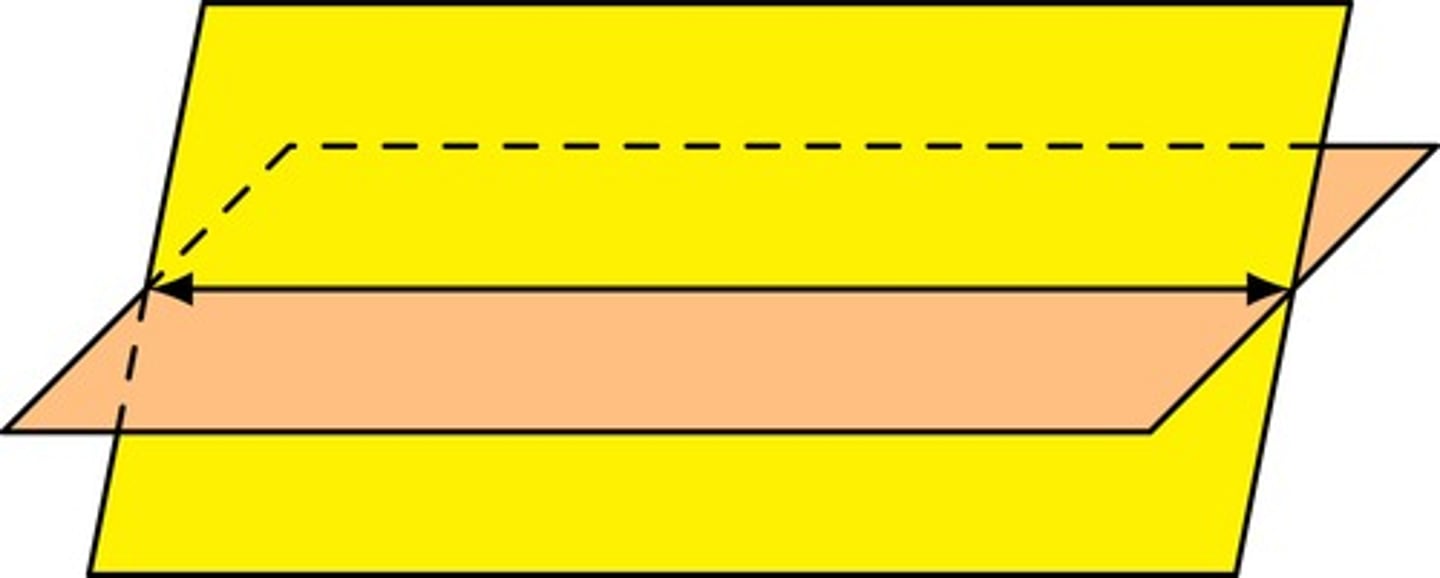
If 2 planes intersect, then their intersection is a ______.

If 2 planes intersect, then their intersection is a line.

Segment Addition Postulate

If point B is between points A and C, then AB + BC = AC.

Ex: AC = 8

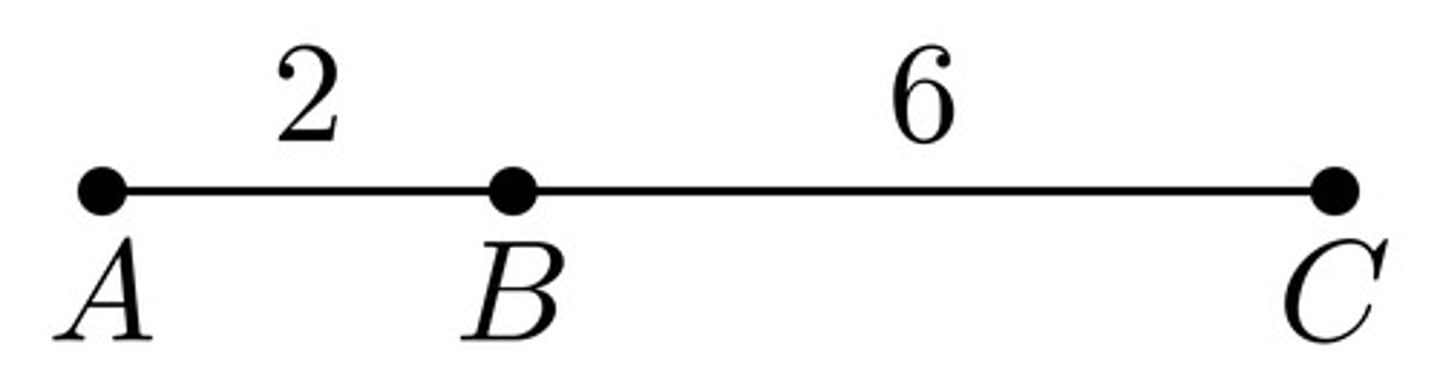
Midpoint Theorem

If M is the midpoint of segment AB, then AM = ½AB and MB = ½AB.