geometry formulas and terms 25

Volume of a prism

B*h

Volume of cylinder

π*r²h

Volume of a cone

1/3π*r²h

Volume of a pyramid

1/3B*h

Volume of a sphere

4/3πr²(h)

population density

pop/area

Density

mass/volume

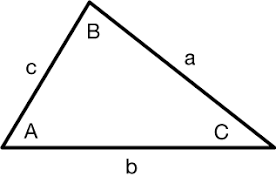
area non right triangle

1/2*absinc

Area of a square

s²

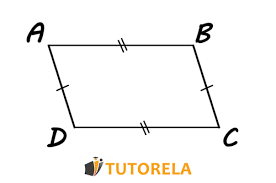
Area of a parallelogram

b*h

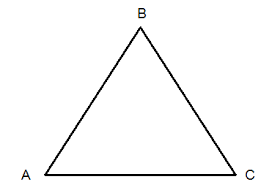
Area of a triangle

1/2b*h

Area of a rectangle

l*w

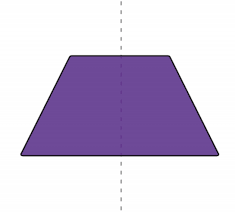
Area of a trapezoid

1/2(b1+b2)h

Area of a circle

π*r²

Area of a rhombus

½ d1*d2

Area of sector of a circle

arc/360*π*r²

Length of an arc

arc/360 π* d

Circumference

π*d

sum of interior angle

180(n-2)

sum of exterior angles

360

One interior angle

180(n-2)/n

One exterior angle

360/n

Pythagorean theorem

a²+b²=c²

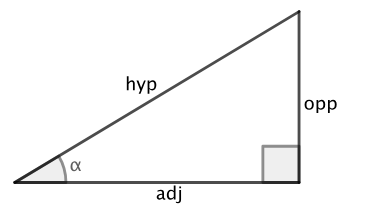
sin

opp/hyp

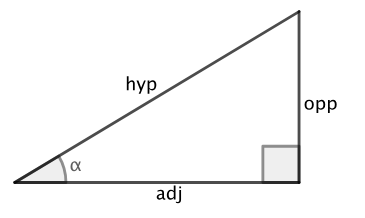
cos

adj/hyp

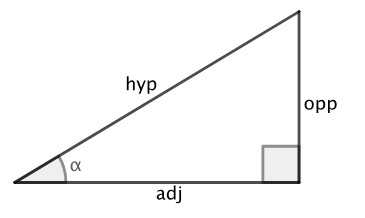
tan

opp/hyp

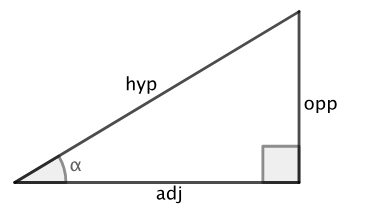
sin x

cos(90-x)

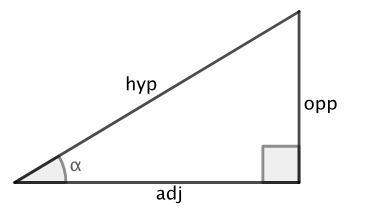
cosx

sin(90-x)

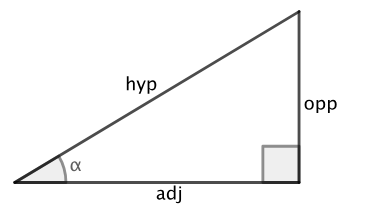
Tanx

cosB(90-x)

r x-axis (x,y)

(x,-y)

r y-axis (x,y)

(-x,y)

r (0,0)

(-x,-y)

r y=-x (x,y)

(-y,-x)

r y=x (x,y)

(y,x)

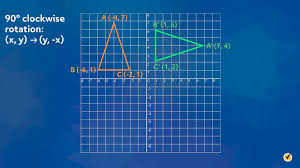
R 90 (x,y)

(-y,x)

R 180 (x,y)

(-x,-y)

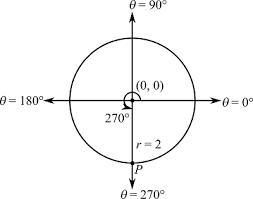
R 270 (x,y)

(y,-x)

Dilation

(x,y)=(kz,ky)

Translation

(x,y)=x+a,y+b)

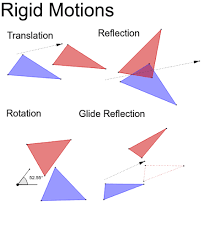
Rigid motion

transformation that preserves distance and angle measure . Translations, reflections and rotations are all rigid motions. Dilations and stretch functions are not rigid motions since they change size

orientation

Order of the letters

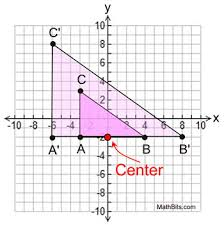
Dilation of a line

When the center of a dilation is not on a line

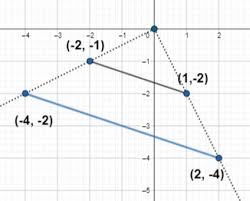
Dilations of a line

when the center on dilation is on line -dilation keeps the line unchanged

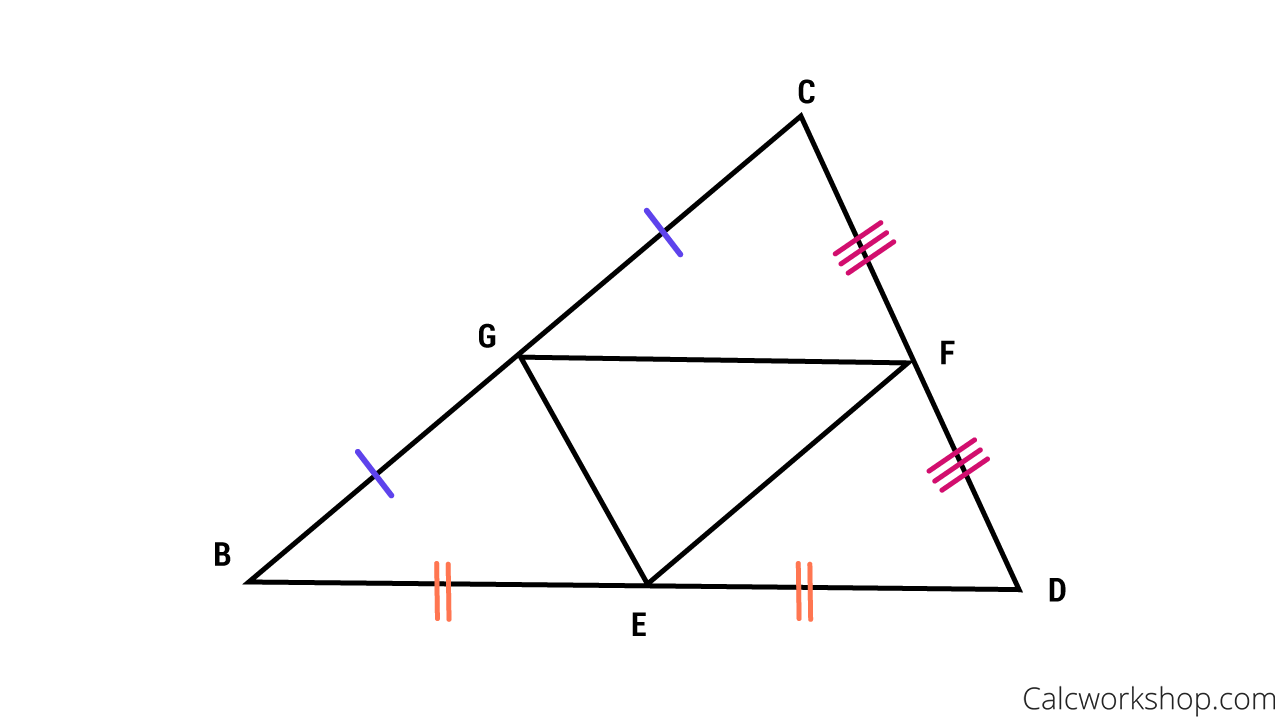
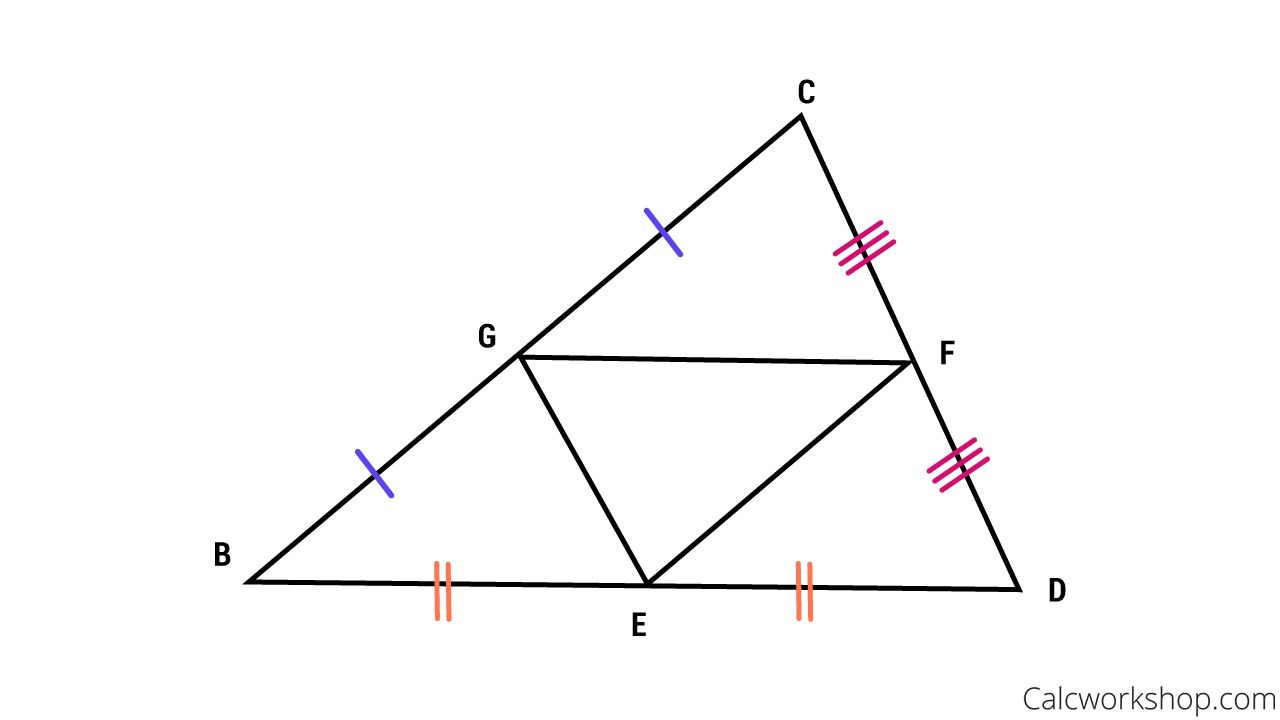
mid-segment theorem

If a line segment joins the midpoints of 2 sides of a triangle

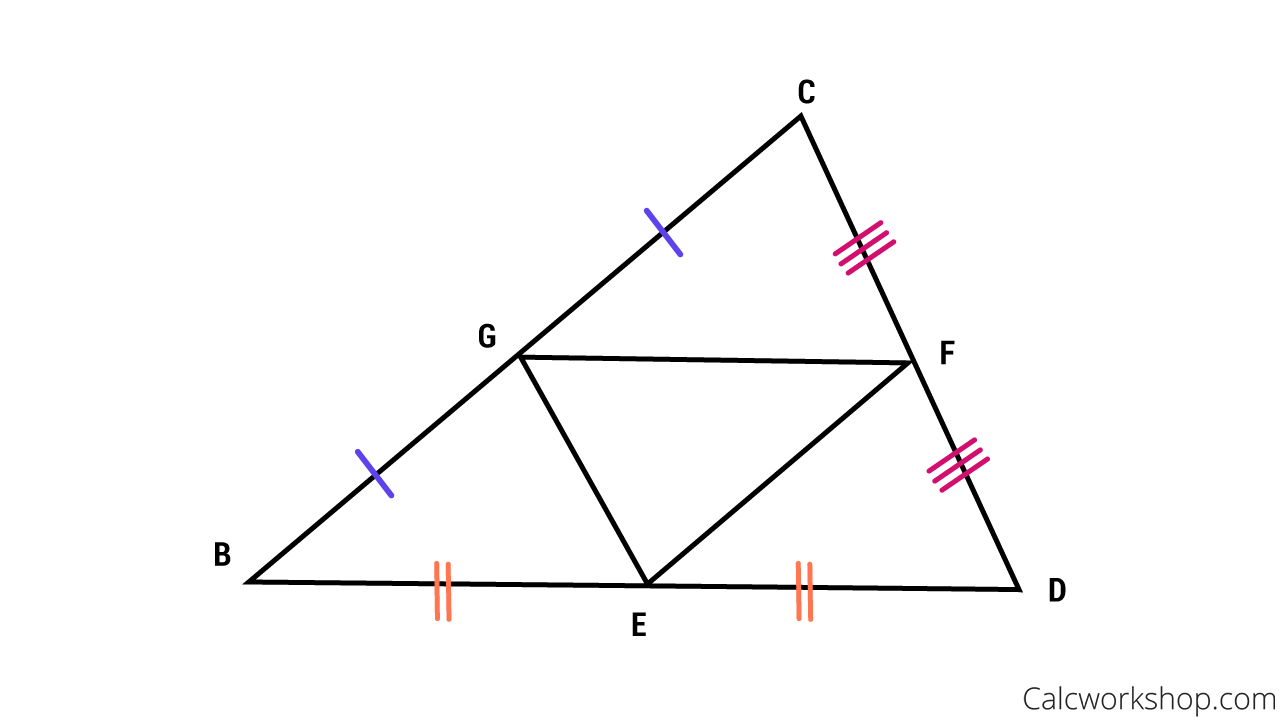
Mid-segment theorem 1

alt/seg1=seg2/alt

Mid-segment theorem 2

leg1/seg1=hyp/leg1

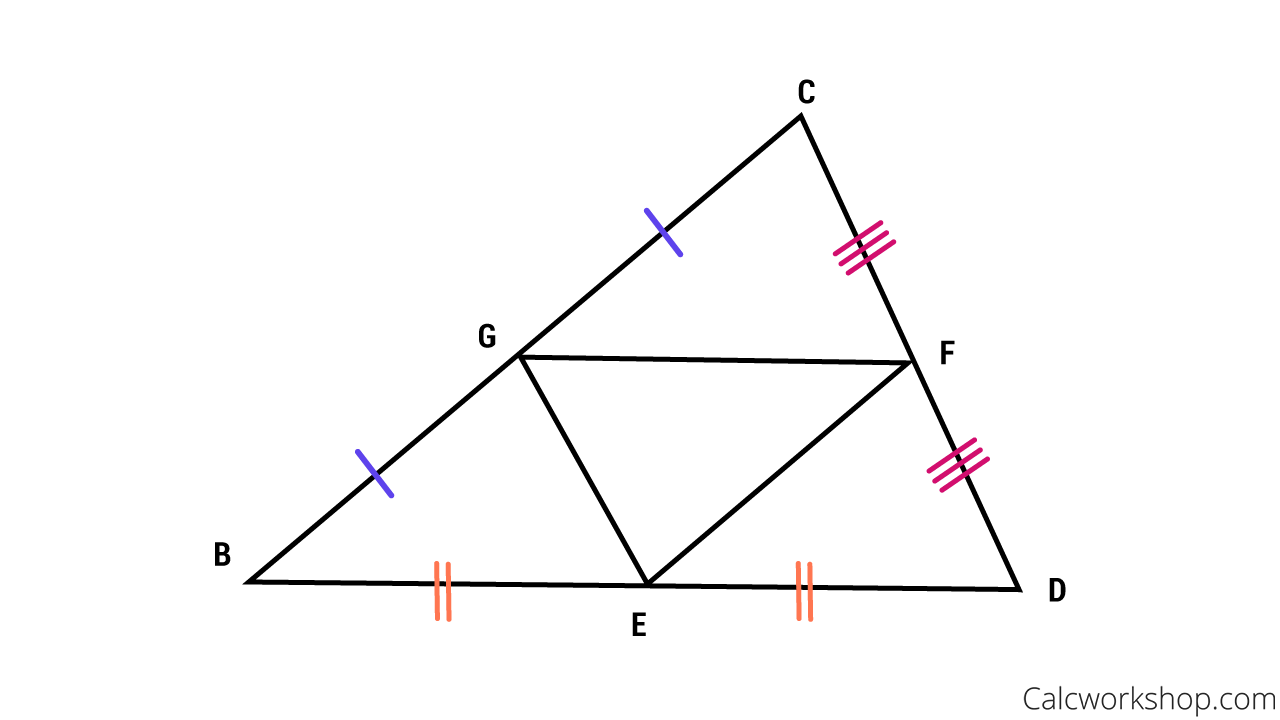
Mid-segment theorem 3

Leg2/seg2=hyp/leg2

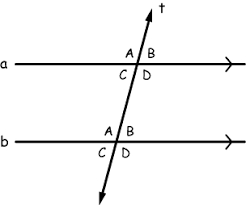
Alt interior angles

<3≅<6,<4≅<5

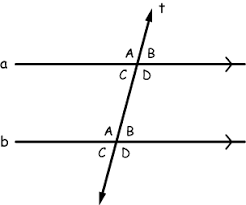
corresponding angles

<1≅ <5,<3≅<7, <2≅<6,<4≅<8

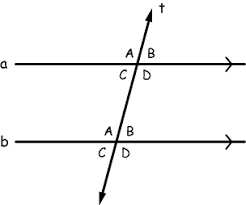
interior angles on the same side of the transversal

<4+<6+180,<3+<5=180

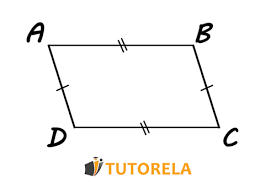
Quadrilaterals , parallelogram

1) Opposite sides are ≅

2) Opposite angels are ≅

3) Opposite sides are parallel

4) Consecutive angels are supplementary

Quadrilaterals, rhombus

1) All properties of a parallelogram

2) Diagonals are perpendicular

3) Diagonals bisect the angels the angels

4) All sides are ≅

Quadrilaterals , rectangle

1) All properties of a parallelogram

Quadrilaterals, Trapezoid

1) Only one pair of opposites side are parallel

Quadrilaterals , Isosceles Trapezoid

1) Only one pair of opposites side are parallel

Quadrilaterals , Square

1) All properties of a rhombus

2) All properties of a rectangle

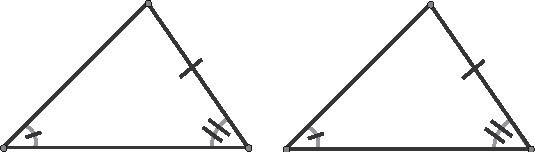
AAS

Angle angle side

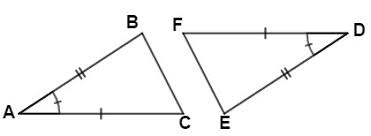
ASA

Angle side angle

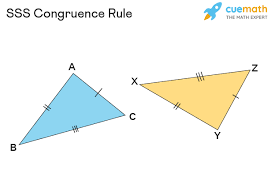
SSS

Side side side

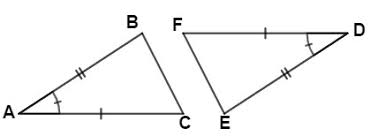
SAS

side angle side

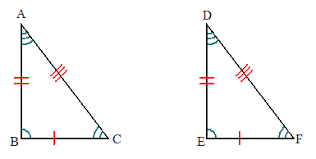
HL

if the hypotenuse and a leg of one right triangle are congruent to the corresponding hypotenuse and leg of another right triangle, then the two triangles are congruent. 

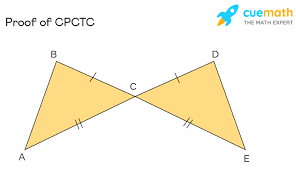
CPCTC

Corresponding parts of congruent triangles are congruent

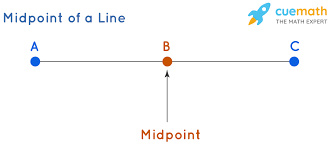
Midpoint

A point on a line that divides it into 2 congruent line segments

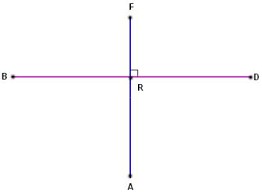
Perpendicular

2 lines that intersect to form right angels

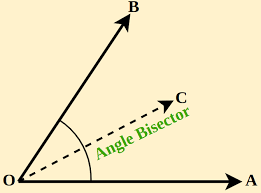
Angle bisector

A line that divides an angle into 2 congruent angles

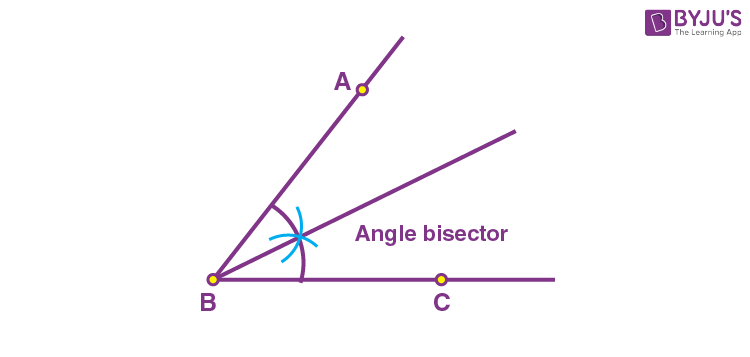
Line bisector

A line that intersects another line at its midpoint

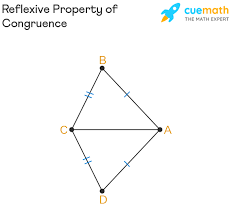
Reflexive

A line or angel that is congruent to itself

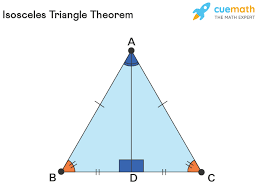
Isosceles triangle theorm

If 2 sides of a triangle are ≅, the then the opposite angles are ≅

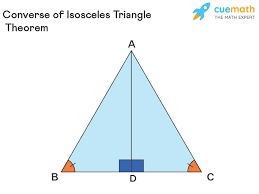
Converse of its isosceles triangle theorem

If 2 angles of a triangle are congruent, then opposite side are ≅

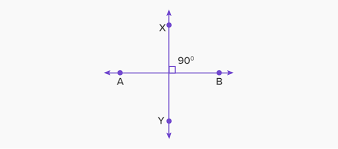
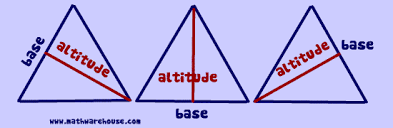
Altitude

A line drawn from the vertex of a triangle to the midpoint of the opposite side

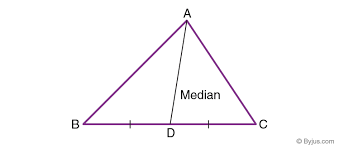
Median

A line drawn from the vertex of a triangle perpendicular to the opposite side

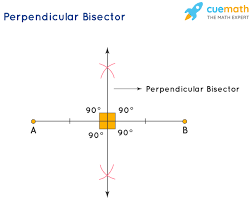
Perpendicular bisector

A line that intersects another line at its midpoint forming right angles

When are triangles ≅?

Triangles are congruent if there is a ridge motion that maps one triangle onto another

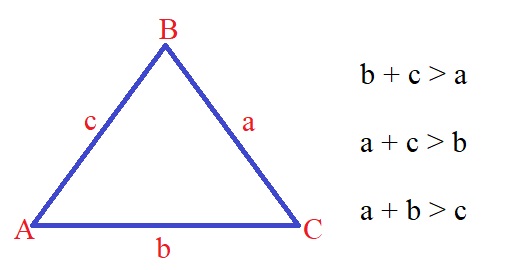
Triangle inequalities

1) Two sides of a triangle must add up to be greater than the third side (b+c>a)

2) The largest angle of triangle is opposite the longest side.(a+c>b)

3) Smallest side- opposite the shortest side (a+b>c)

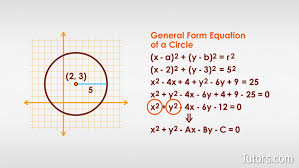
Equation of a circle

1) x²+y²=r² center=(0,0) & radius =r

2) (x-h)² = r² center=(h,k) & radius = r

To find the center and radius of a circle by completing the square

1) Group the x’s together, the y’s together & leave a space

2) Move the constant to the opposite side

3) Take ½ of the coefficient of x, square it and add to both sides. Do the same for coefficient of y

4) Factor

Distance

d= √((x₂ - x₁)² + (y₂ - y₁)²)

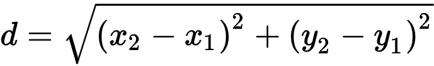
Midpoint

m=(x1 + x2)/2, (y1 + y2)/2)

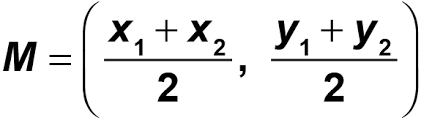
Slope

m = (y₂ - y₁) / (x₂ - x₁)

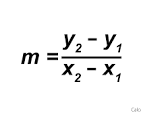
Partitioning a segment in the ratio

a:b -

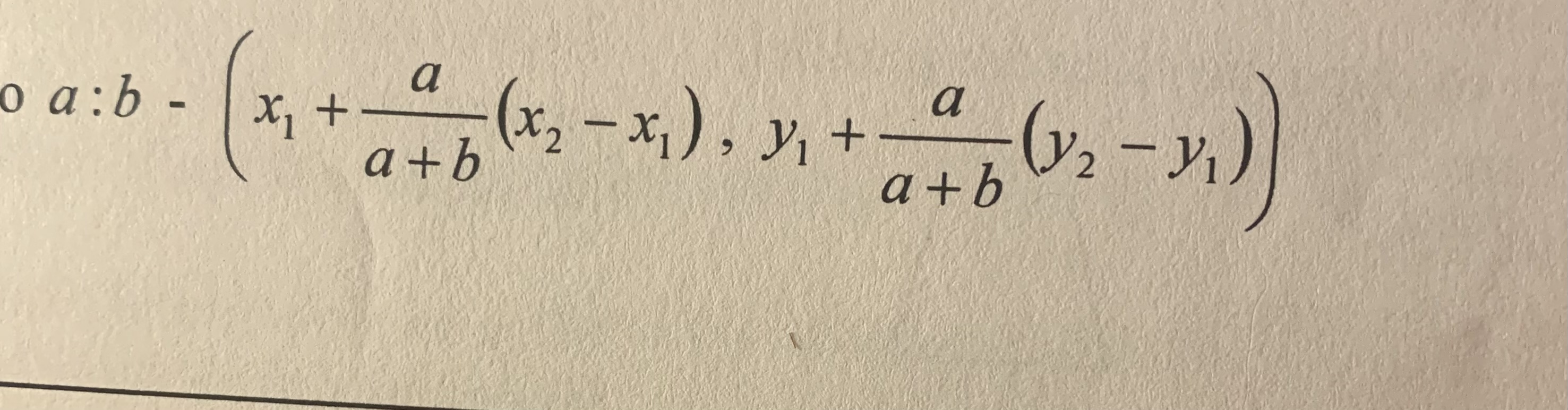
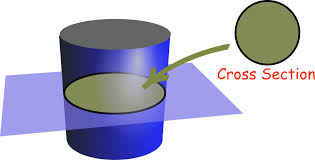
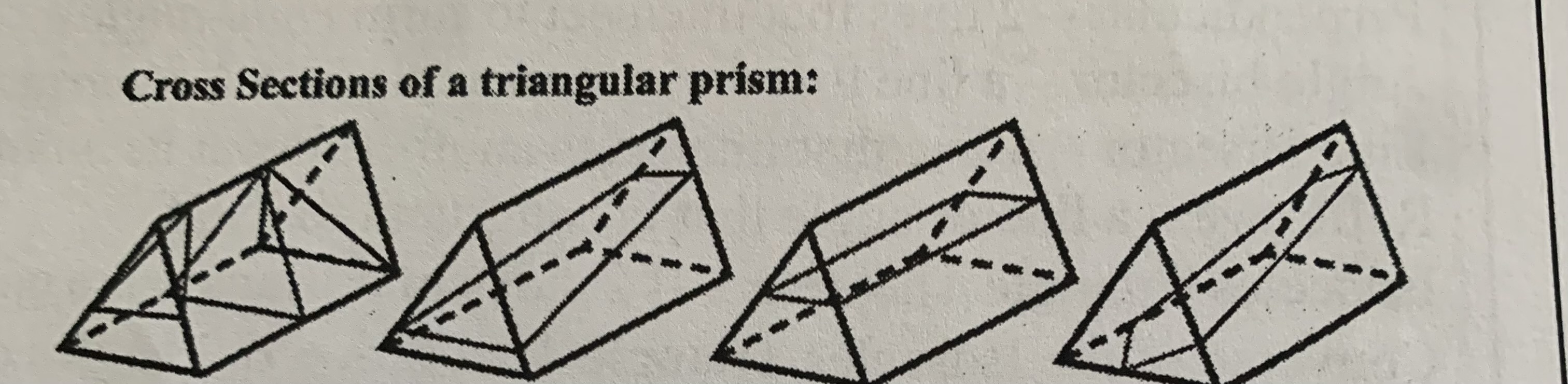
Cross section

A 2-dismensoinal figure that is created when a plane is passed through through a polyhedron

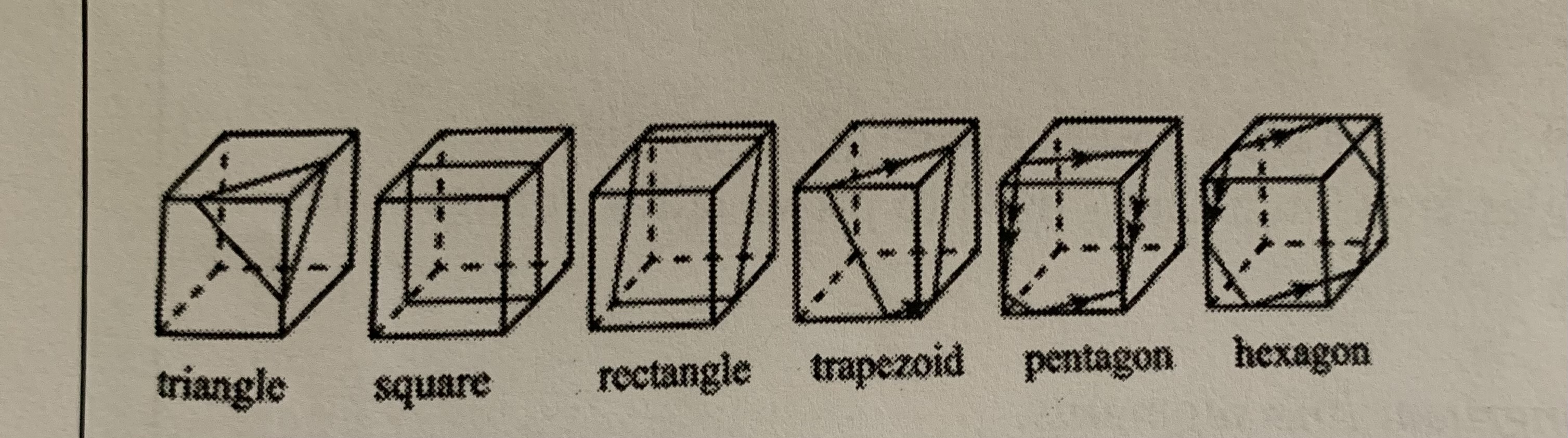
Cross sections of a cube

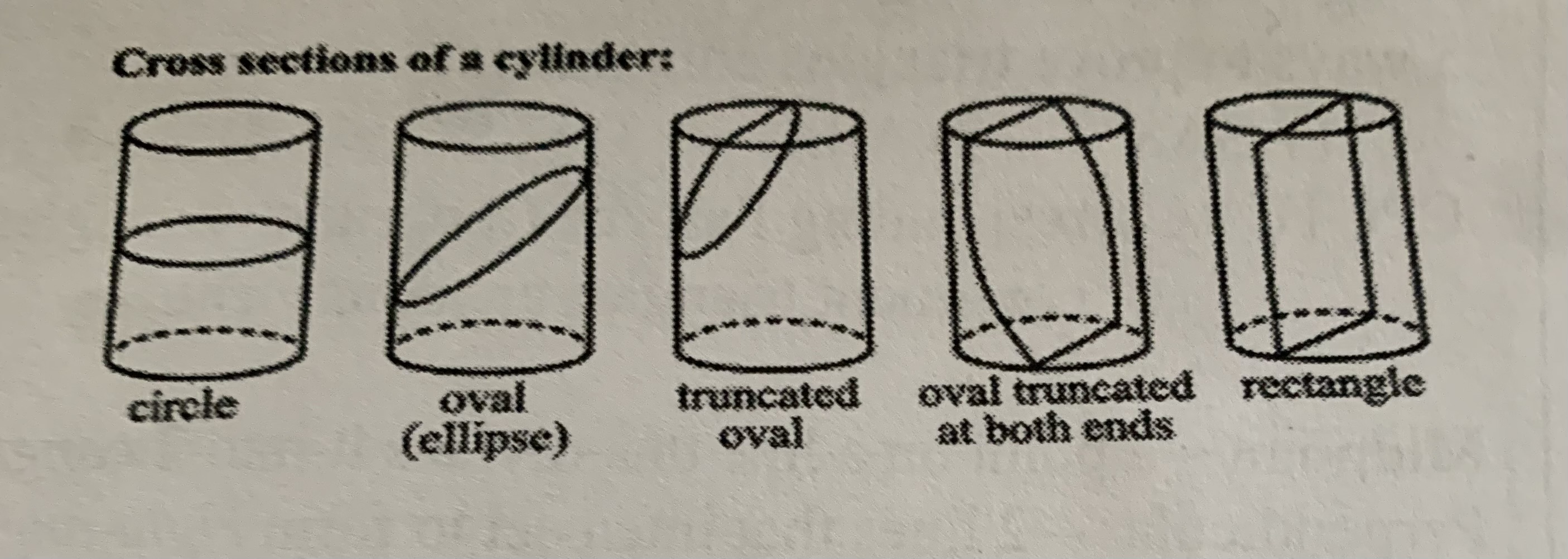
Cross sections of a cylinder

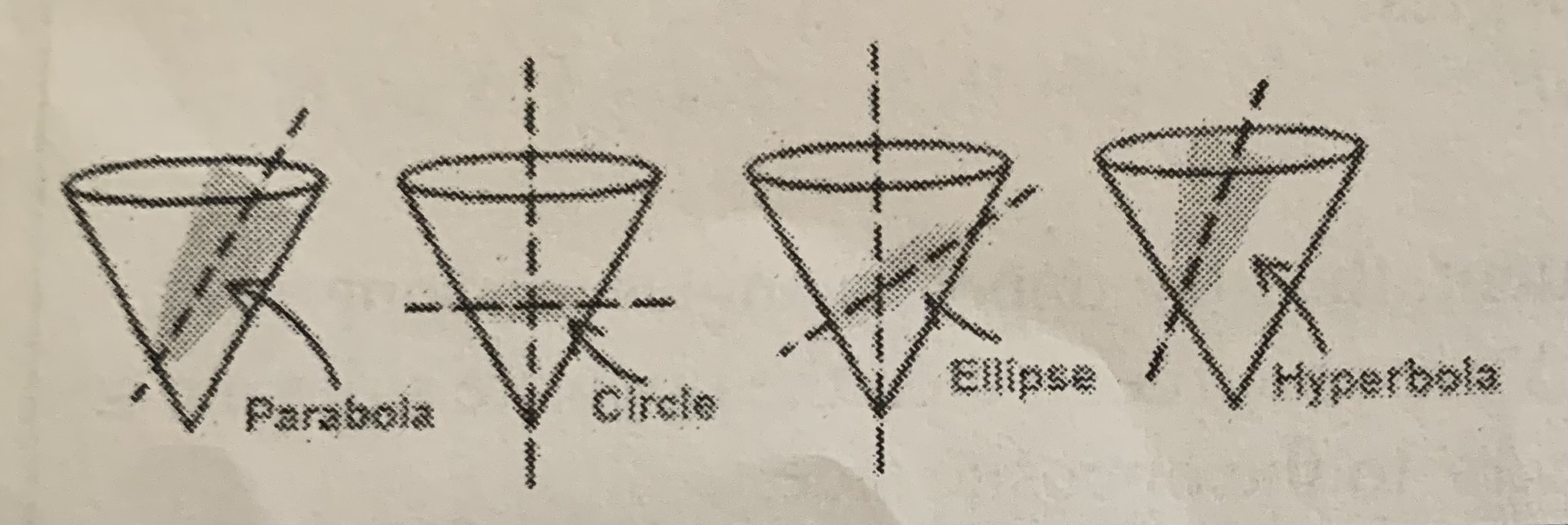
Cross sections of a cone

Cross sections of a triangular prism

Special right triangles 1

30-60-90

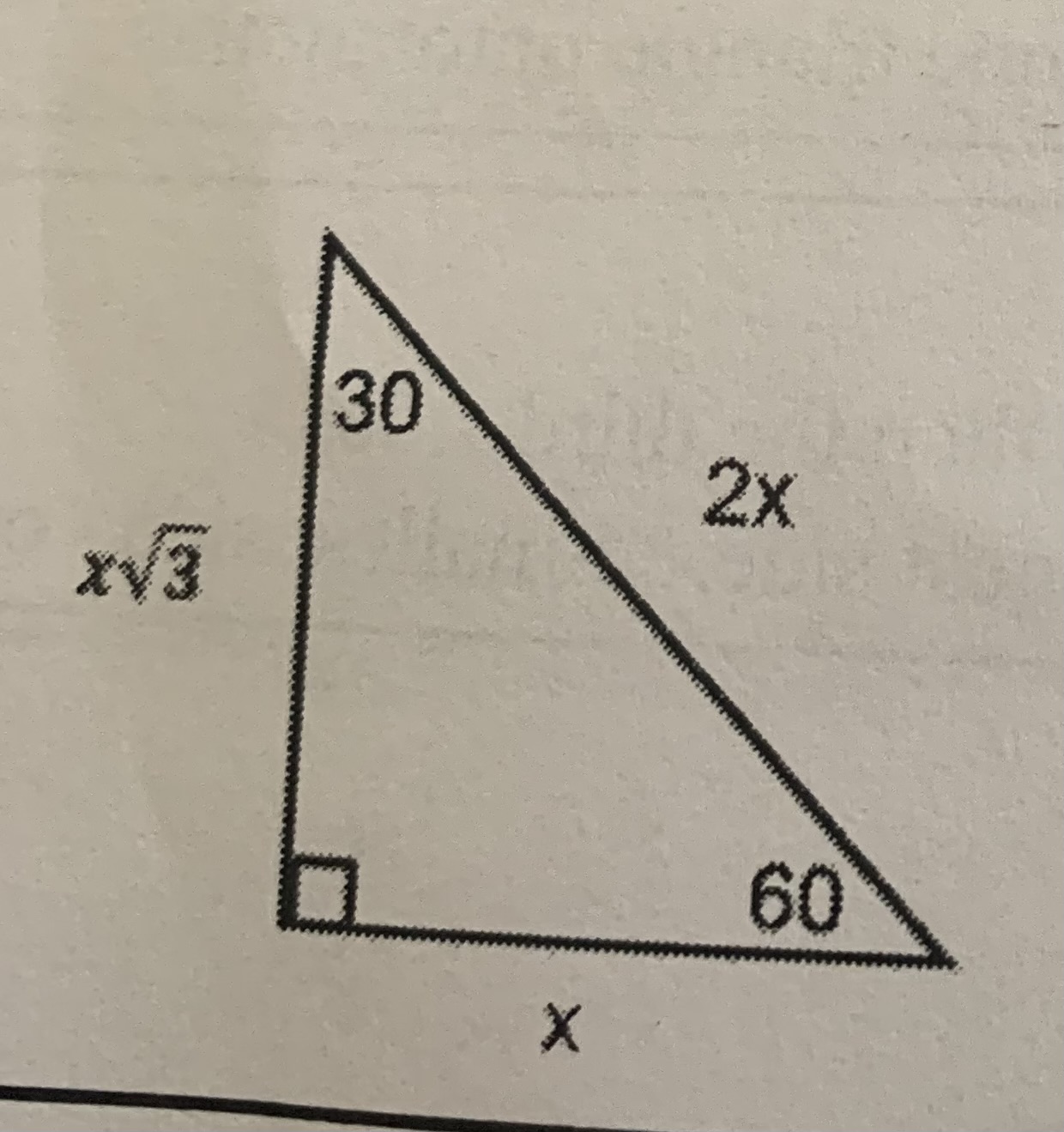
Special right triangles 2

45-45-90

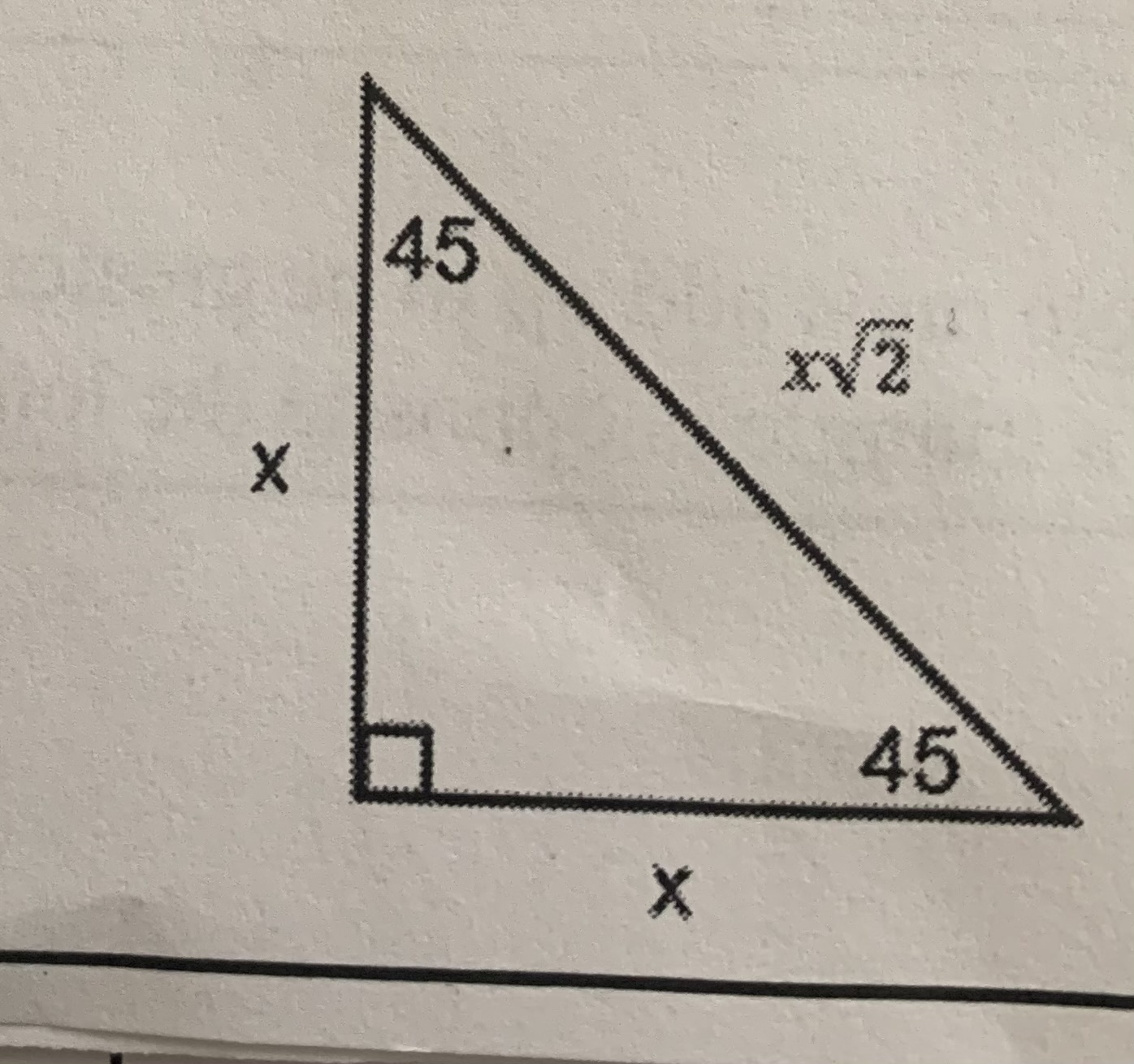
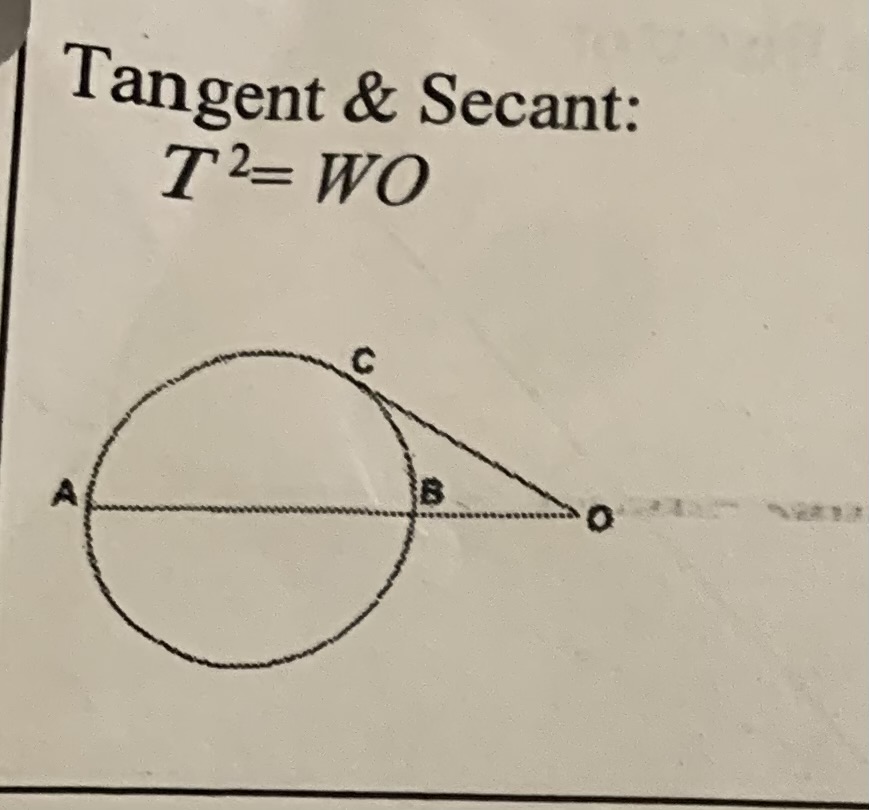
Tangent &secant

T²=WO

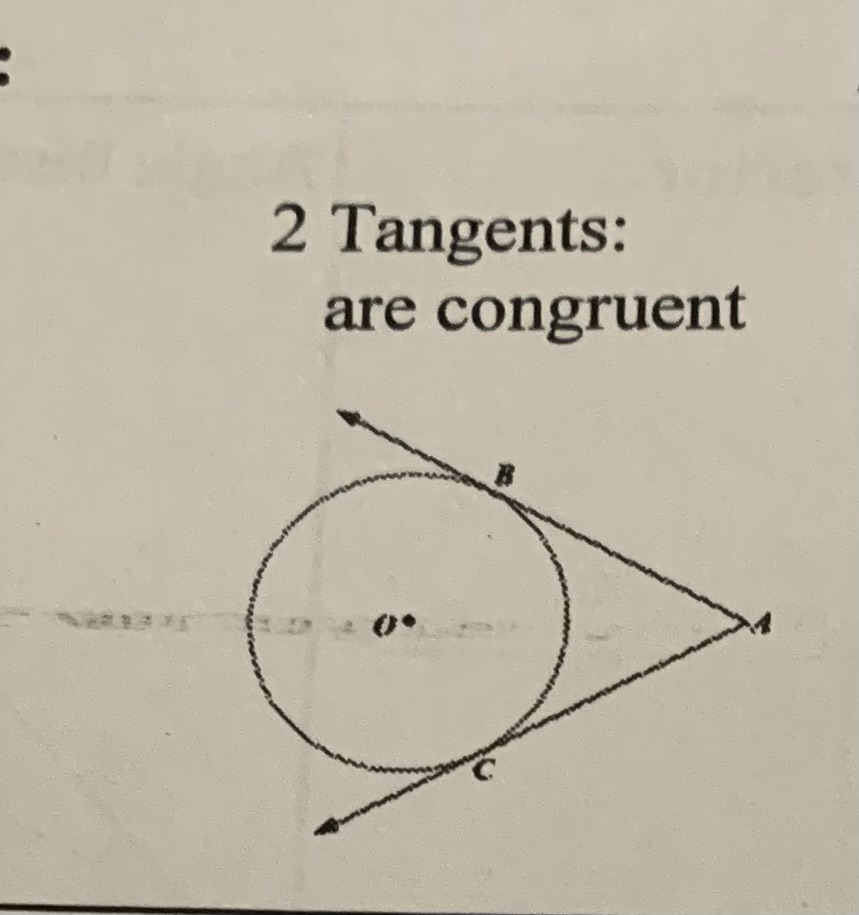
Tangent

Are congruent

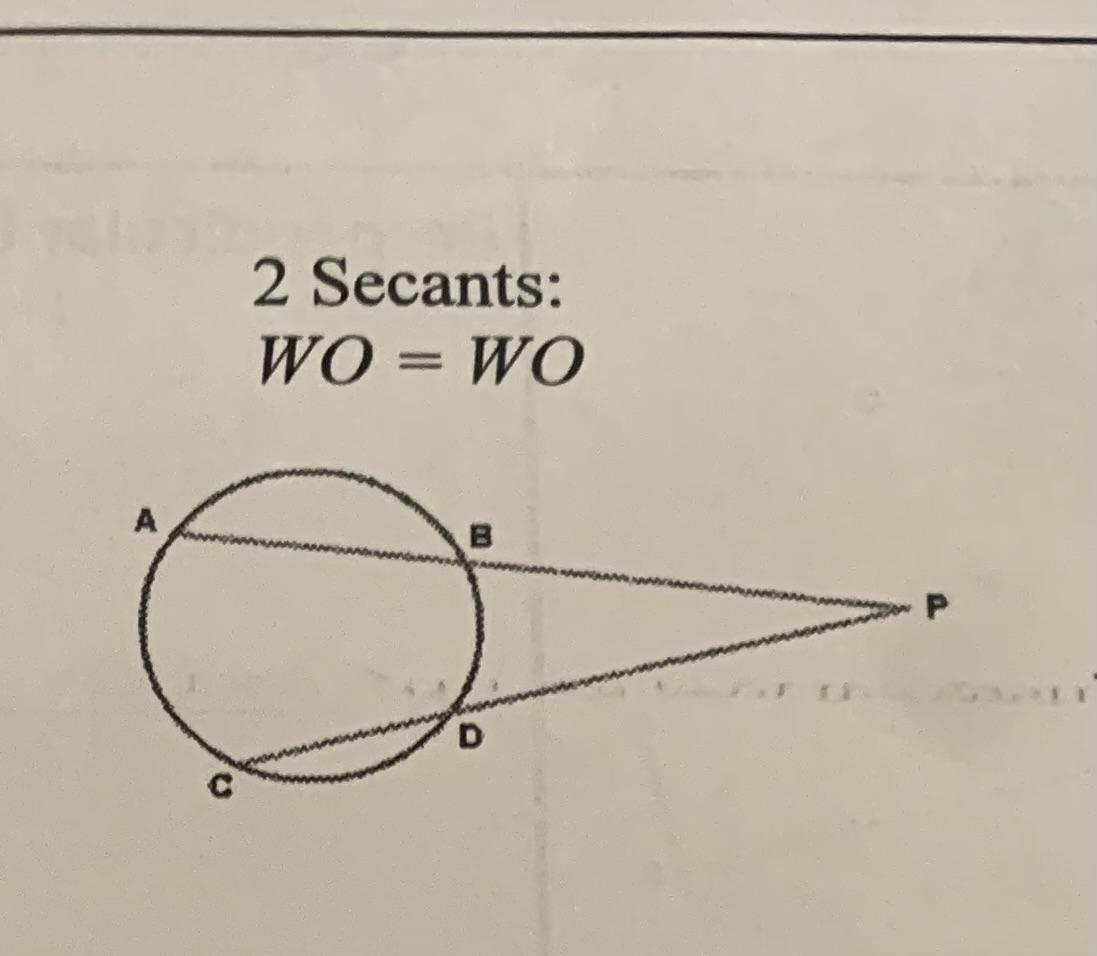
Secants

WO=WO

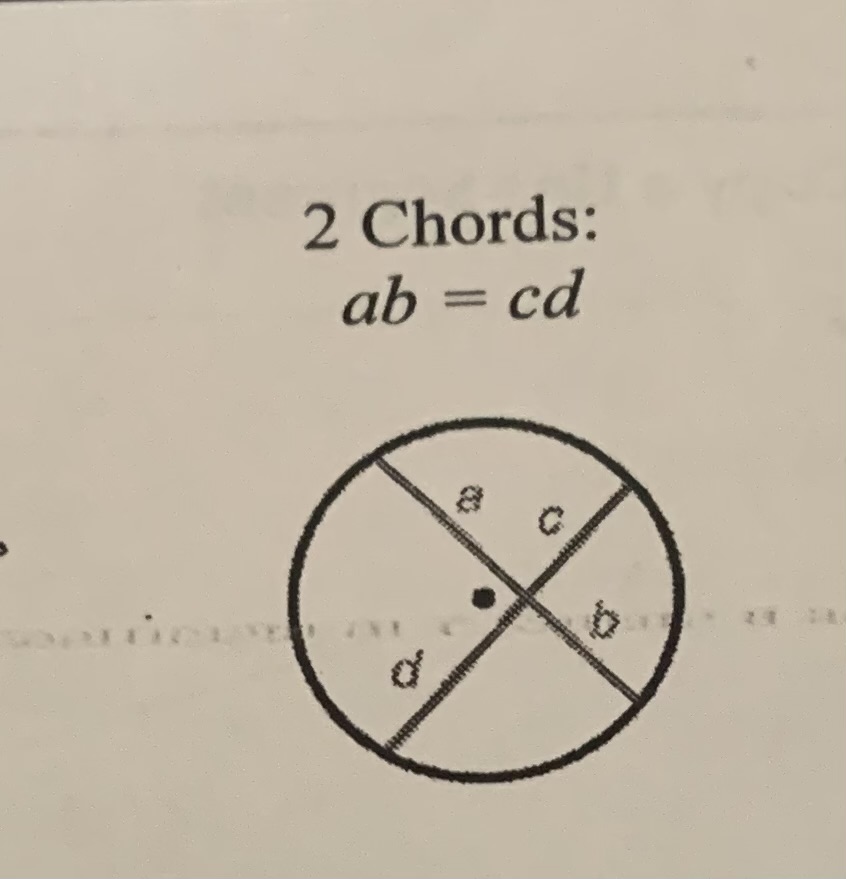
Chords

ab=cd

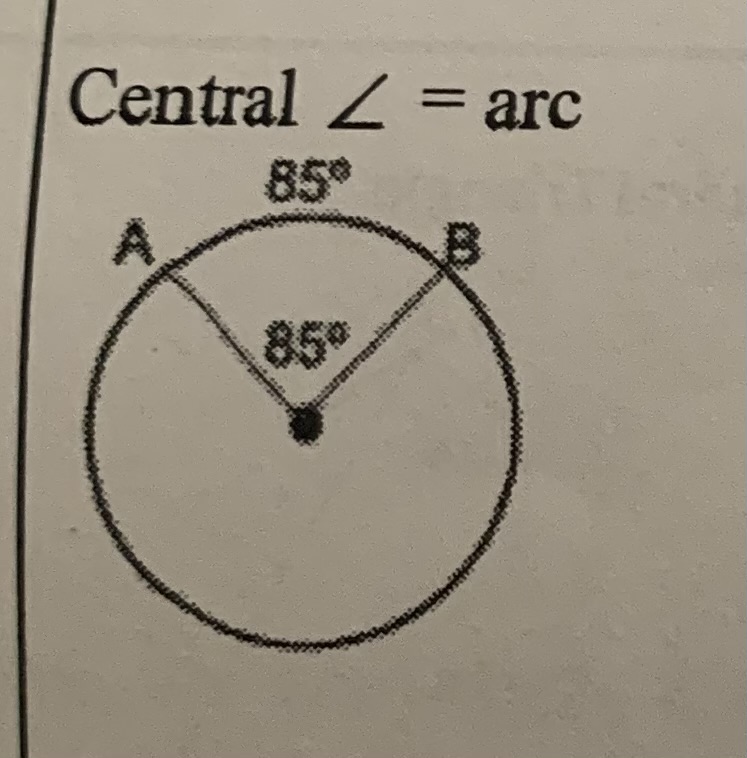
Central circle

= arc

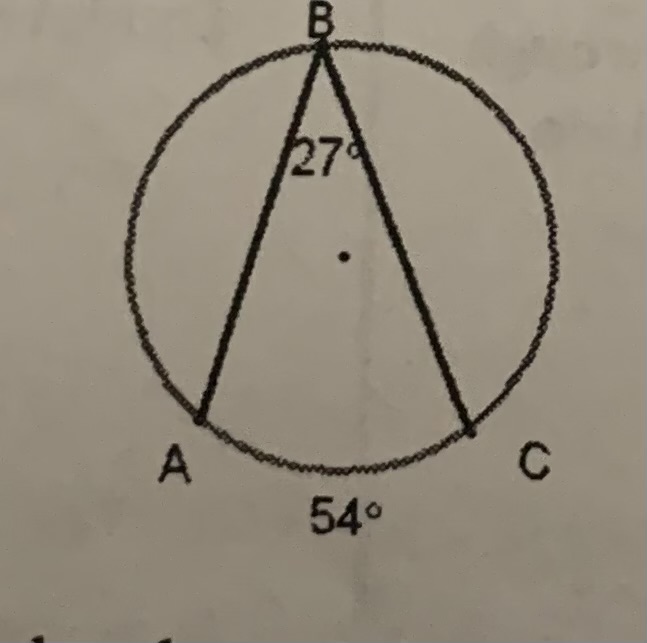
Inscribe circle

½ arc

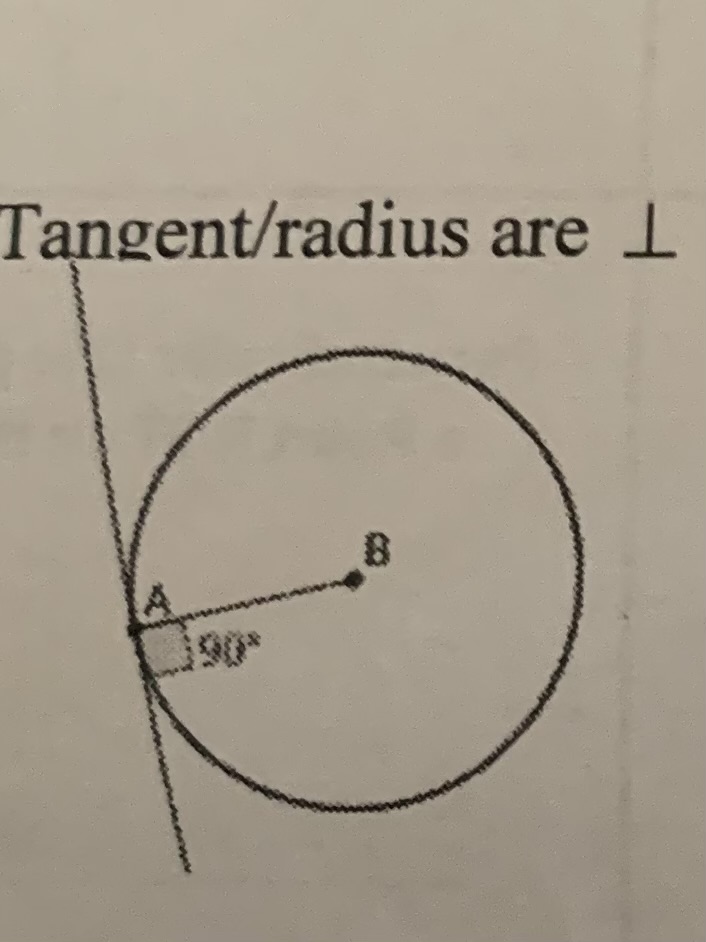
Tangent/radius circle

are ⊥

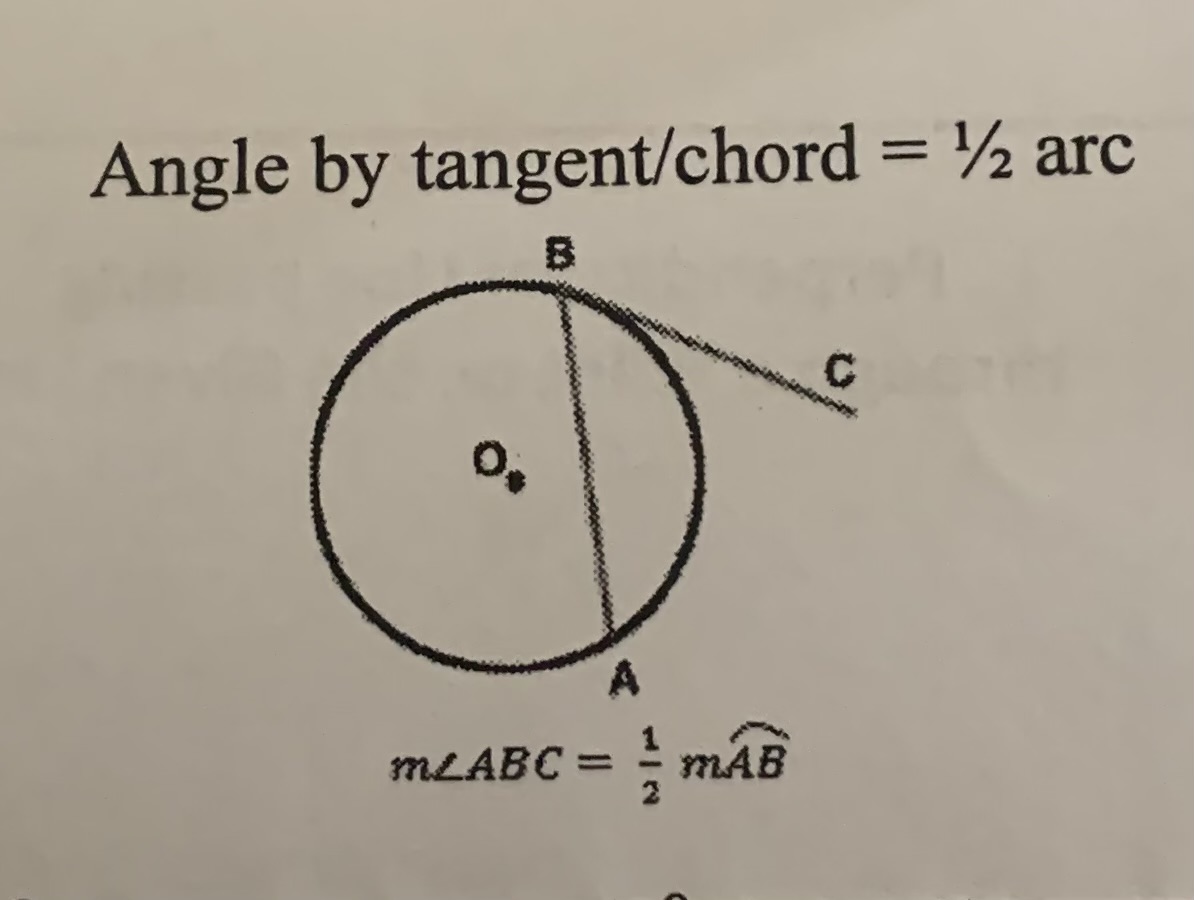
Angle by tangent/chord

=1/2 arc

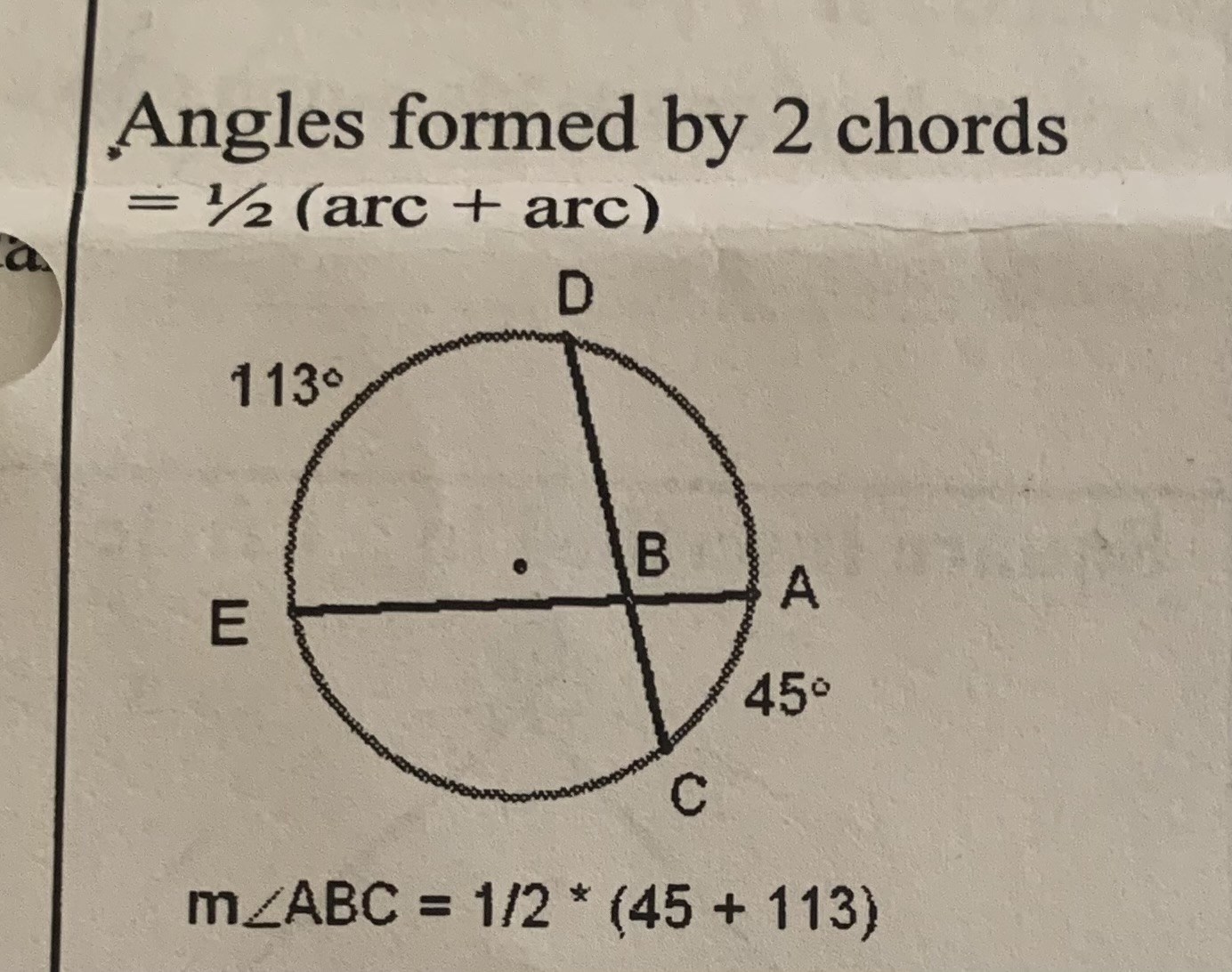
Angeles formed by 2 chords

½ (arc+arc)

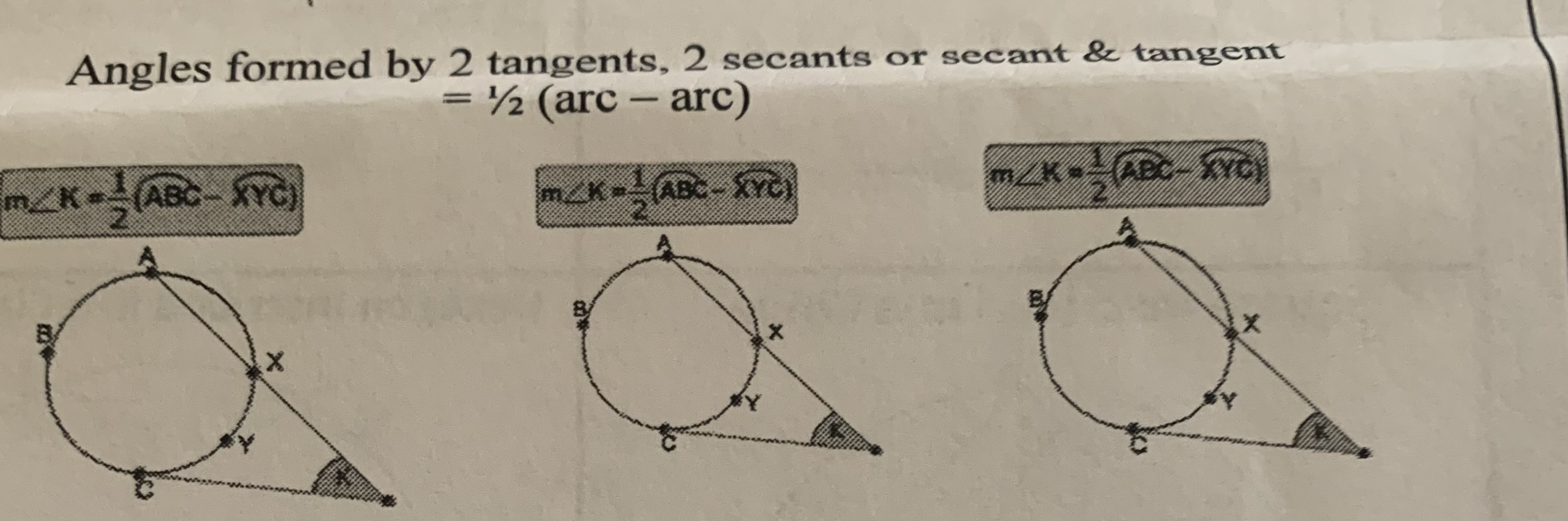
Angles formed by 2 tangents,2 secants or secant &tangent

=1/2(arc-arc)

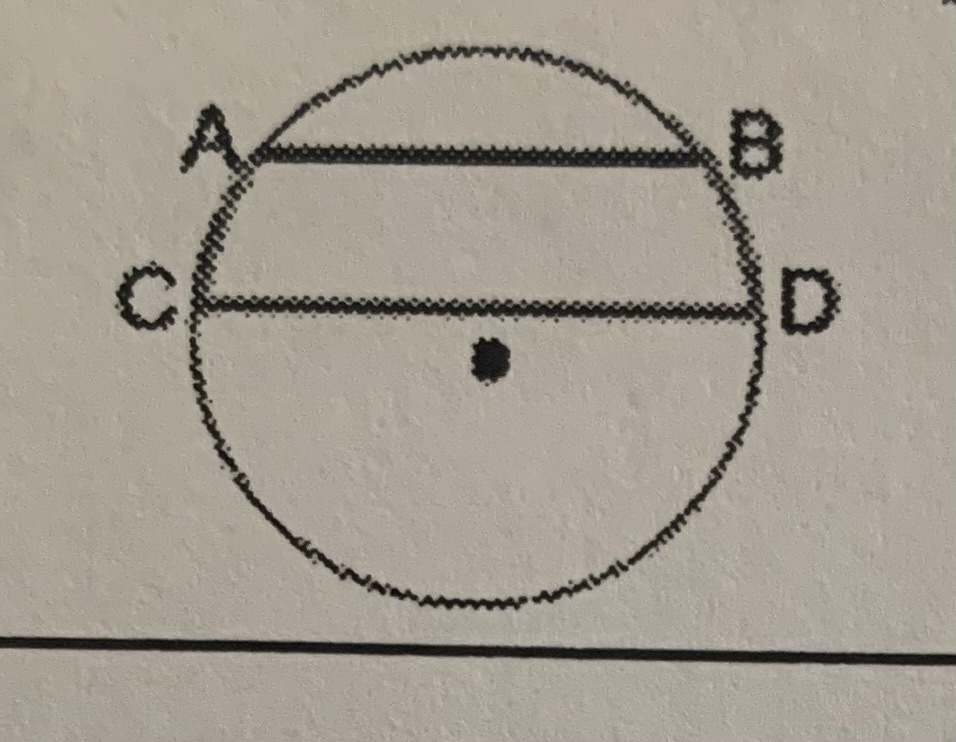
Parallel chords intercept congruent arcs

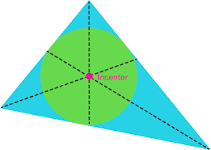
Incenter

Angle bisectors meet always inside the tringle It’s equidistant from the sides

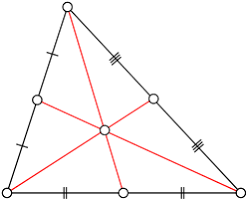
centroid

Medians meet always inside the triangle makes 2;1 ratio