Intro to AI - First Order Logic

What are Propositional Logic Limitations?

• Stating similar facts is cumbersome

  • Can’t make generalizations

• In propositional logic, world contains facts, not objects

  • Ontological commitment of PL is limited

Propositional Logic vs Natural Language

Natural language deals with objects (nouns) and relations (verbs), hence is more expressive

Facts vs Objects

Fact: Felix is a cat, Garfield is a cat, Nemo is a fish, Garfield is a cat implies Garfield has whiskers

Object: Felix, Garfield, Nemo, Dory, Reef, Indiana

Properties, Relations (Predicates)

Cat, Fish, Swims, HasWhiskers, Lives

Cat(Felix), Cat(Garfield)

Fish(Nemo), Fish(Dory)

Lives(Nemo, Reef), Lives(Garfield, Indiana)

Generalizations

For all X, if Cat(X) then HasWhiskers(X)
“All cats have whiskers”

For all X, if Fish(X) then Swims(X)
“All fishes can swim”

First Order Logic (FOL) World consists of ___?

Objects, Reactions, Functions

First Order Logic (FOL) Sentences are made up of

Symbols, Connectives, Quantifiers and Variables

Symbols

for constant objects, predicates, and functions

Connectives

as in propositional logic

Quanitifiers and variables

Ɐx, Ǝy

Constants

• Refer to objects, unlike propositional var referring to propositions

• EX. John, Richard, C, L1, L2

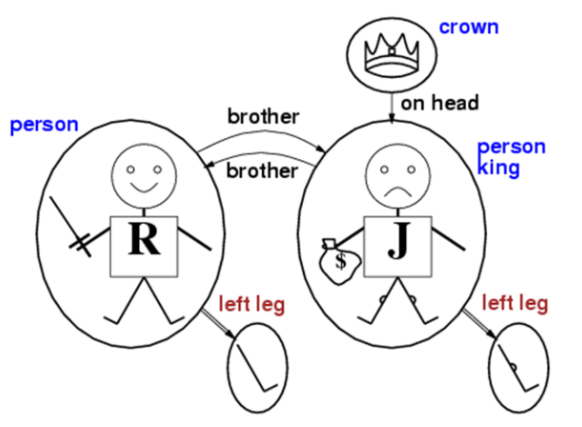
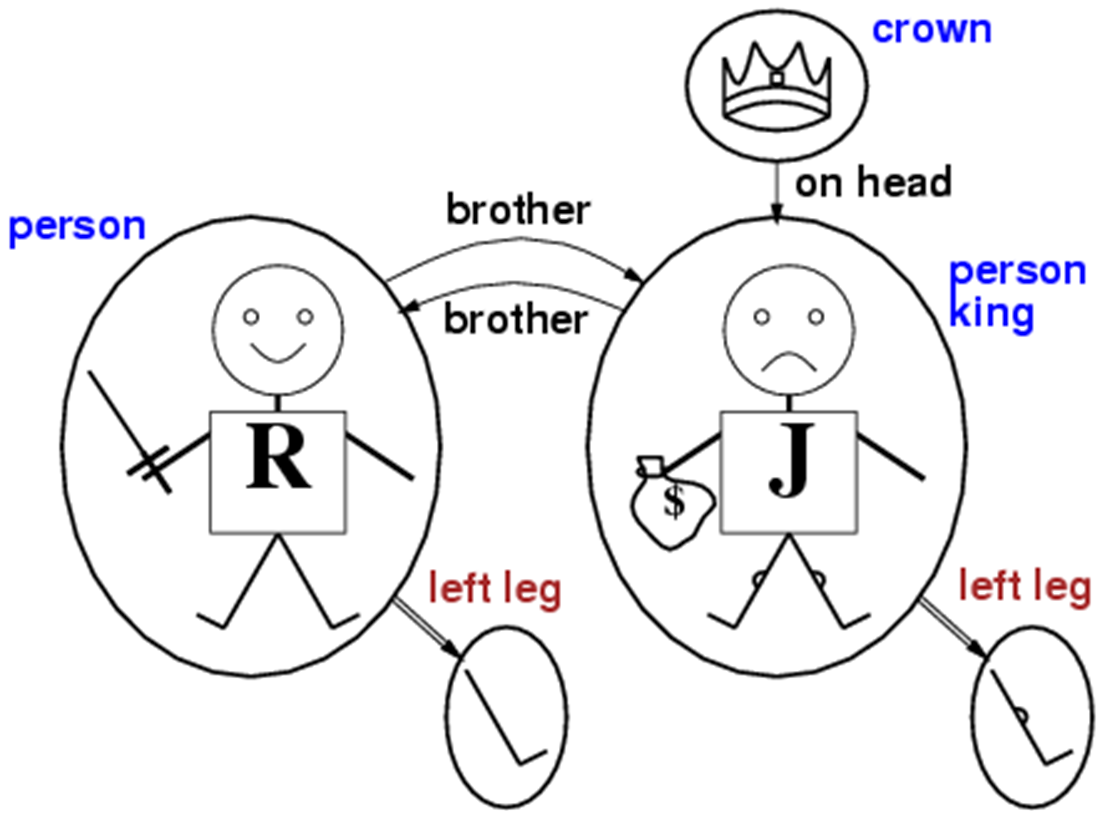
Name the predicates in this example

• Person = {John, Richard}

• King = {John}

• Crown = {C}

• Brother = {(John, Richard), (Richard, John)}

• OnHead = {C, John}

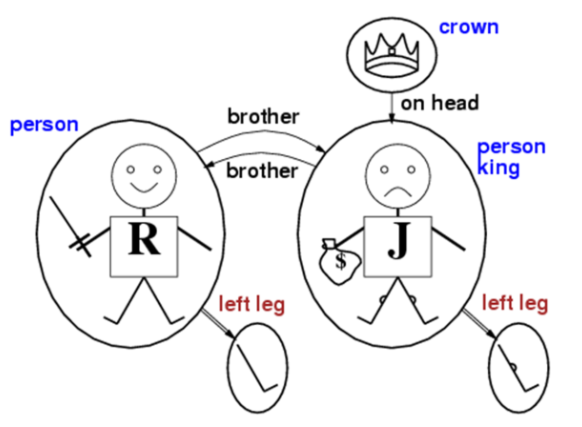
Name the Functions in this example

• LeftLeg={(Richard->L1),(John->L2)}

• Strictly speaking, the function should be total—all objects should have a value when the function is applied to it

Models in FOL

• Consists of the objects (domain elements) and relations (including functions)

  • Conceptual view of the world

Interpretations in FOL

• Associates the symbols to the objects, relations and functions in the model

  • Number of interpretations for a given set of symbols is combinatorially explosive

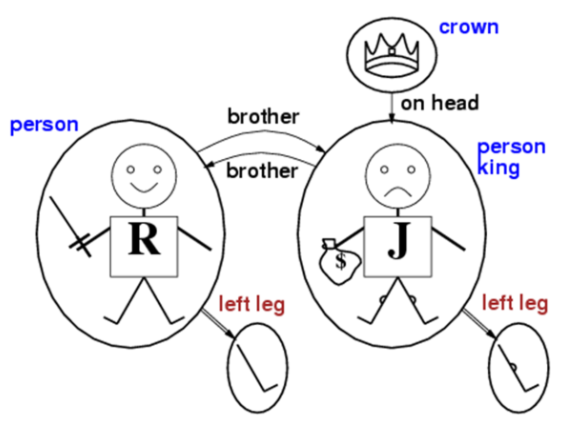
Given this example, what are the sentences you can make?

• Person(John) ∧ Person(Richard)

• OnHead(C, John)

• LeftLeg(John) = L1 ∨ LeftLeg(Richard) = L2

• ∀x King(x) ⇒ Person(x)

Term

• Expression that refers to an object

• EX. Richard

• EX. LeftLeg(John)

Atomic Sentences

Constructed by equating terms (=) or by a predicate (with terms as arguments)

Complex Sentences

Sentences with connectives or quantifiers

What are the possible forms of a sentence in FOL?

• Atomic Sentence

• (Sentence Connective Sentence)

• ¬Sentence

• Quantifier Variable Sentence

What are the types of Terms in FOL?

• Function-Symbol(Term, …)

• Constant-Symbol

• Variable

What do Connectives represent in FOL?

Logical operations combining sentences

List the main Connectives in FOL

∧ (and), ∨ (or), ⇒ (implies), ⇔ (if and only if)

What are the Quantifiers in FOL?

∀ (for all), ∃ (there exists)

Semantics

• Truth of a sentence in FOL:

  • Determined with respect to a model and an interpretation

  • Analogous notions for entailments, validity and satisfiability

• Model enumeration is impractical in FOL

Types of Quantifiers

1. Universal Quantification

2. Existential Quantification

Universal Quantification

• ∀x P is true in a model m iff P is true with x being each possible object in the model

• A conjunction of instantiations

Existential Quantification

• ∃x P is true in a model m iff P is true with x being some object in the model

• A disjunction of instantiations

Universal Quantification for this example

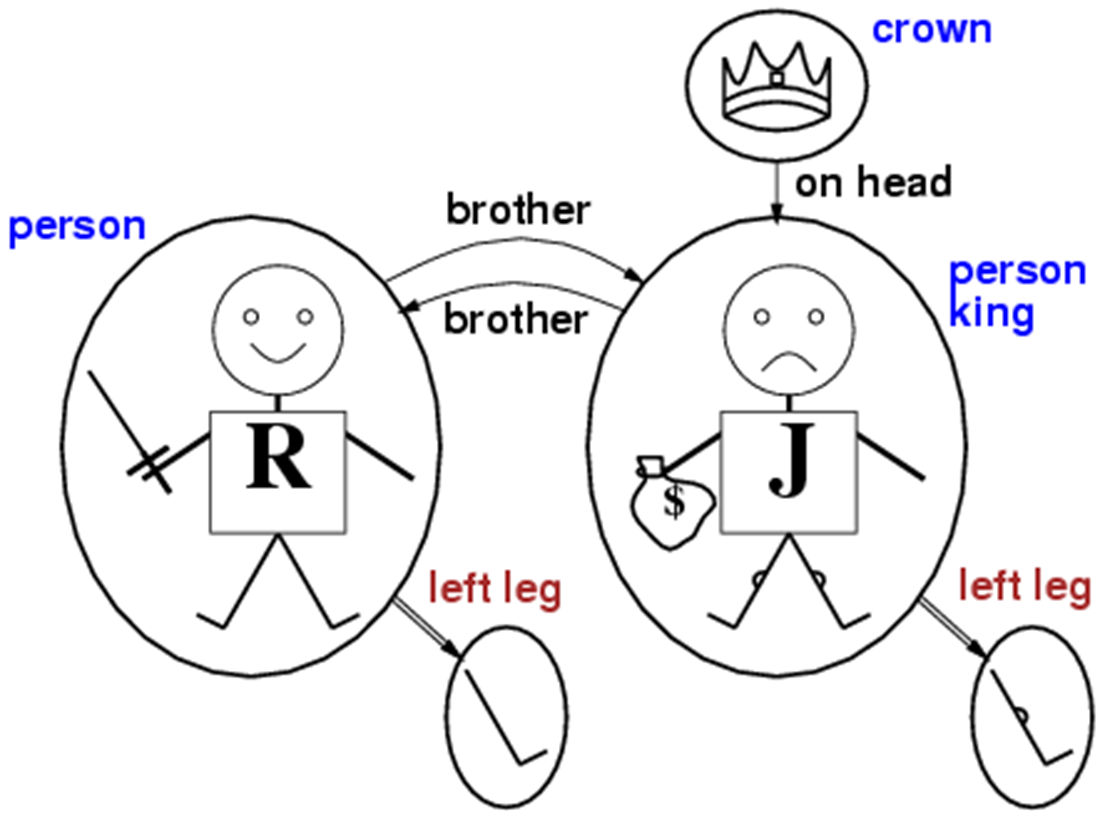
• ∀x King(x) ⇒ Person(x)

  • Means that King(x) ⇒ Person(x) holds for all objects
    (e.g., John, Richard, C, L1,L2)

  • (King(John) ⇒ Person(John)) ∧ (King(Richard) ⇒ Person(Richard)) ∧ (King(C) ⇒ Person(C)) ∧ (King(L1) ⇒ Person(L1)) ∧ (King(L2) ⇒ Person(L2))

Existential Quantification for this example

• ∃x Crown(x)
  “there is at least one crown”

  • Means that for one of the objects (e.g., John, Richard, C, L1,L2), Crown(x) holds

  • Crown(John) ∨ Crown(Richrd) ∨ Crown(C) ∨ Crown(L1) ∨ Crown(L2)

Translate to english: ∀x King(x) ⇒ Person(x)

“All kings are persons”

Translate to english: ∃x Crown(x)  ∧ OnHead(x,John)

“John has a crown on his head”

Translate to english: ∀x∀y Brother(x,y) ⇔ Brother(y,x)

“The ’Brother’ relationship goes both ways”

Translate to english: ∃x∃y Brother(x,Richard) ∧ Brother(y,Richard) ∧ ¬(x=y)

“Richard has at least 2 brothers”

Translate to english: ∀x King(x) ⇒ ∃y Crown(y) ∧ OnHead(y,x)

“All kings have crowns”

Properties of Quantifiers: Nested Quantifiers

• ∀x ∀y P  equivalent to  ∀y ∀x P

• ∃x ∃y P  equivalent to ∃y ∃x P

• Does not apply if quantifiers are different

Properties of Quantifiers: De Morgan's law of quantifiers

• ∀x ¬P ≡ ¬∃x P

• ∀x P ≡ ¬∃x ¬P

• ∃x ¬P ≡ ¬∀x P

• ∃x P≡ ¬∀x ¬P

Turn this into logic: Everybody loves somebody

∀x∃y Love (x, y)

Turn this into logic: There is somebody that everybody loves

∃x∀y Love (y, x)

What to look out for in quantifiers?

• Using quantifiers (∀, ∃) in combination with ∧, ⇒

• The domain consists of multiple kinds of objects

Translate this to english: ∀x King(x) ⇒ Person(x)

“All kings are persons”

Translate this to english and is it true or false: ∀x King(x) ⇒ Person(x)

“All kings are persons”

True

Translate this to english and is it true or false: ∀x King(x) ∧ Person(x)

“Everything in the world is a king and a person”
False

Translate this to english and is it true or false: ∃x Crown(x) ∧ OnHead(x,John)

“There is a crown on John’s head”

True

Translate this to english and is it true or false: ∃x Crown(x) ⇒ OnHead(x, John)

“There is an object where this rule holds”

Almost always true

Functions vs Predicates

• Functions map objects to one another

• Predicates describe properties of objects

Functions

• Returns an object; this object is a term

• Serves as a noun phrase

• FatherOf(x) returns whoever is x’s father

• Sum(4,3) returns 7

Predicates

• Returns a truth value; result of a formula

• Serves as a verb phrase, which can be an atomic sentence

• Father(x,y) means x is the father of y

• EqualTo(Sum(4,3), 7) evaluates to True

Is this ok: ∃x LeftLeg(x)

not ok because LeftLeg is a function

Is this ok: ∃x LeftLeg(John) = x

ok since it compares a function value (LeftLeg(John)) to an object (x)

Is this ok: ∃x LeftLeg(x) = L1

ok because it’s a valid equality — the function LeftLeg(x) returns an object, and you’re checking if that object equals L1

Is this ok: ∃x Crown(x)

ok because Crown is a predicate

Common error between Functions and Predicates

• Treating a function (returns an object) like a predicate (returns a true/false value)

  • Often, because = was omitted

• LeftLeg(John) = L1 ∨ LeftLeg(Richard) = L1
  “L1 is either John’s or Richard’s left leg”

FOL in Wumpus World

• Represent Wumpus World more compactly

  • Less sentences to represent rules

  • Capture rules on pits and breezes, Wumpus and stenches

• Can include time and percept objects in the world

  • Percept is represented as a list of constant symbols

  • Predicates with time arguments capture the dynamic nature of the agent moving in this world

Inference Algorithms in FOL

• Reduction to propositional inference (propositionalization)

• More efficient methods:

  • Lifting and unification

  • Resolution

  • Can be demonstrated in Logic programming languages like prolog

Propositional Logic VS First Order Logic

While PL deals with logical symbols, FOL deals with objects, relations, and functions

Translate this to FOL: Cottonball loves fish

Loves(Cottonball, Fish)

Translate this to FOL: Emilio is a student

Student(Emilio)

Translate this to FOL: Drea studies Computer Science

Students(Drea, CS)

Which natural language statement is the best interpretation of: ∃y ∀x Loves(x, y)?

There is a specific person whom everybody loves.

Choose the FOL notation which uses a function correctly to represent: "Alice's father is older than Bob."

OlderThan(FatherOf(Alice), Bob)

Translate to english: Loves(Buddy, Tasha) ∧ ~Loves(Tasha, Buddy)

Buddy loves Tasha but Tasha doesn’t love Buddy.

Which natural language statement is the best interpretation of: ∀x (Cat(x) ∨ Dog(x))?

Everything is either a cat or a dog.

Which natural language statement is the best interpretation of: ∃x (Apple(x) ∧ Red(x) ∧ ∃y (Box(y) ∧ In(x, y)))?

There is an apple that is red and in a box.

Which natural language statement is the best interpretation of: ∀x (Car(x) → ¬∃y (HasWheel(x, y) ∧ Three(y)))?
(Assume Three(y) means y is the number 3)

No cars have three wheels.

Which FOL notation best represents the statement: "All students like music."

∀x (Student(x) → Likes(x, Music))