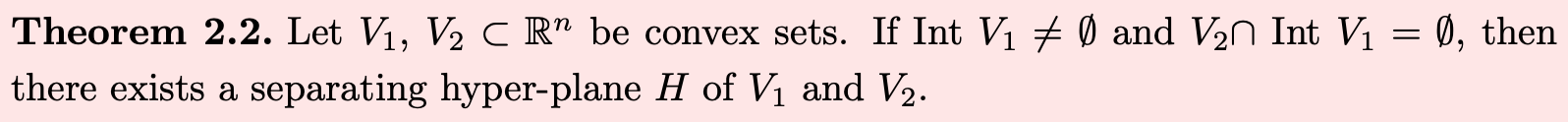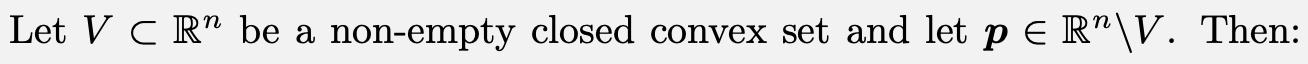1 - convexity & hyperplanes

Convex sets

Geometric Definition

Convex sets

Algebraic Definition

Convex sets

Interpretation

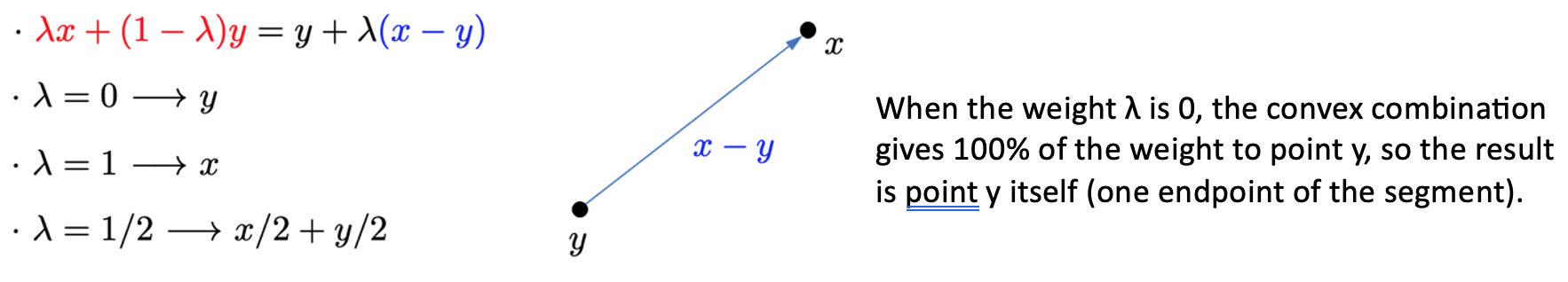
Convex sets

Example

Convex sets

Altenative Definition

Convex combinations

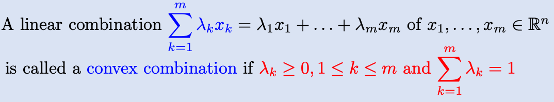
Convex combinations

Example

Theorem

Convex combinations
V is convex

Properties of Convex Sets

Convex Functions

Geometric Definition

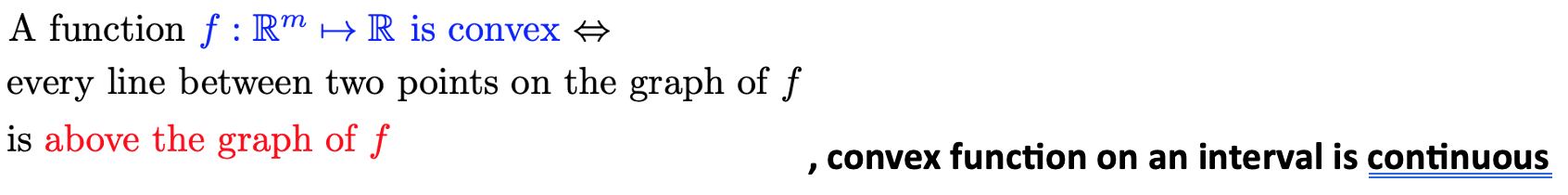
Convex Functions

Algebraic Definition

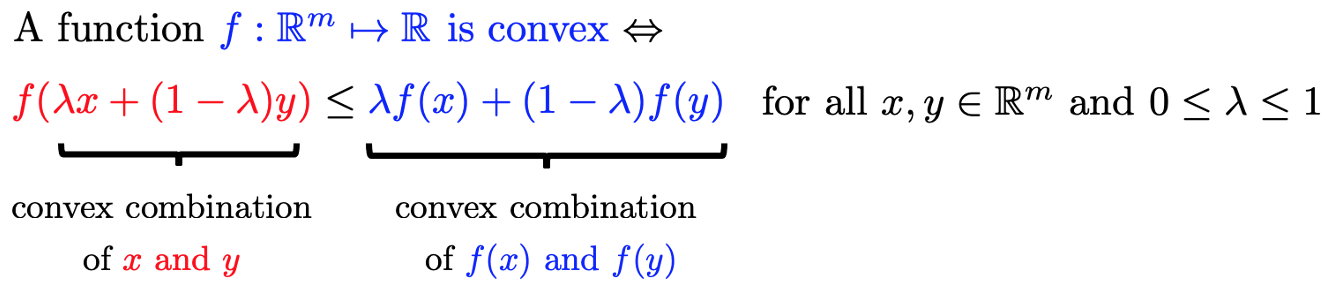
Convex Functions

Epigraph

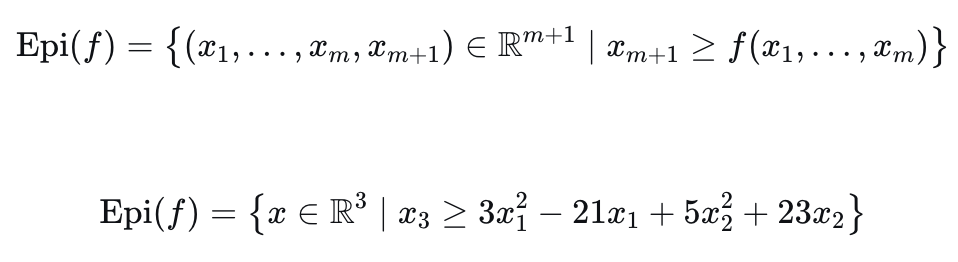
Show that g assumes a global minimum of value m_V on V as well as a global maximum of value M_V on V

The set V is compact, since V is closed, and by part 1 V is bounded. The map g is continuous since it is affine.

Applying the property ”A continuous function on a compact 2 set assumes a global minimum and a global maximum” gives that g assumes a global minimum m_V and a global maximum M_V on V .

Properties of Convex Functions

Properties of Concave Functions

Properties of concave functions are very similar to convex,

as a function f is concave if and only if -f is convex.

Useful inequalities

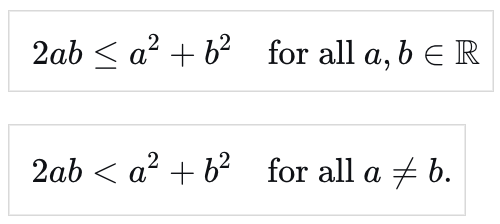
Strictly Convex Functions

Algebraic Definition

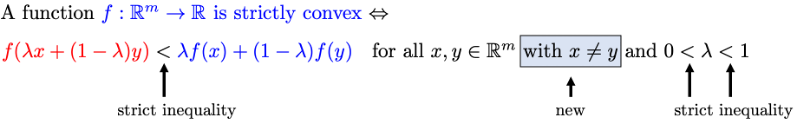
Strictly Convex Functions

Example

Strictly Convex Functions

Proving blueprint 1

Strictly Convex Functions

Proving blueprint 2

Level set of a function =

Quasi-convex Functions

Define the map φ : R → R, piecewise function

Hypo graph of f

A function f is concave if and only if its hypograph is a convex set.
(Compare: A function f is convex if its epigraph is convex.)

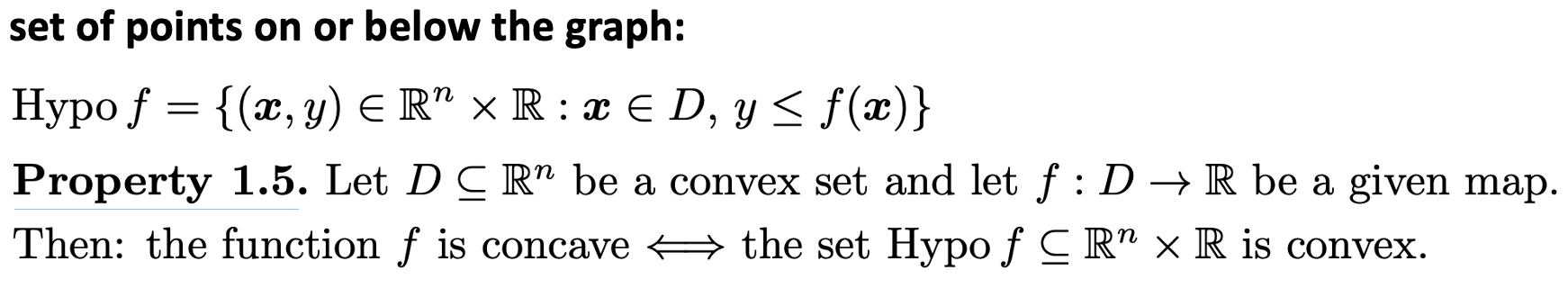
Balls Notation Reminder

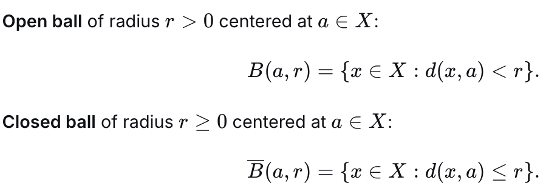
Hyperplane

Separating Hyperplane

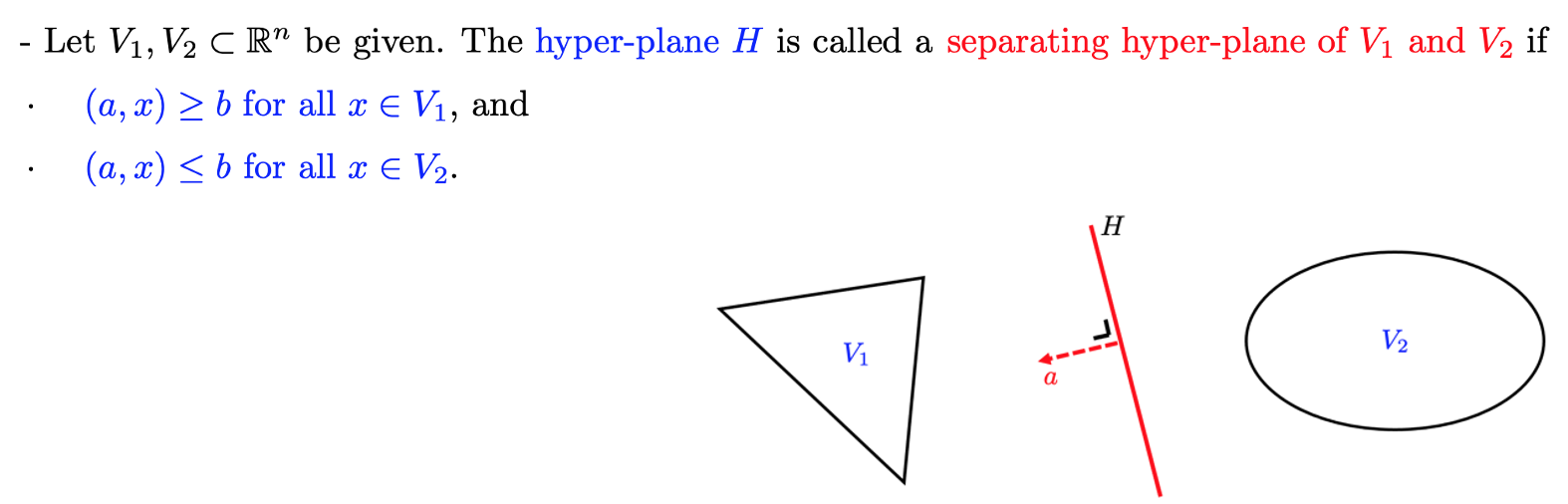
Alternative definition Convexity

using separating hyperplanes

Separation Theorem (duality)

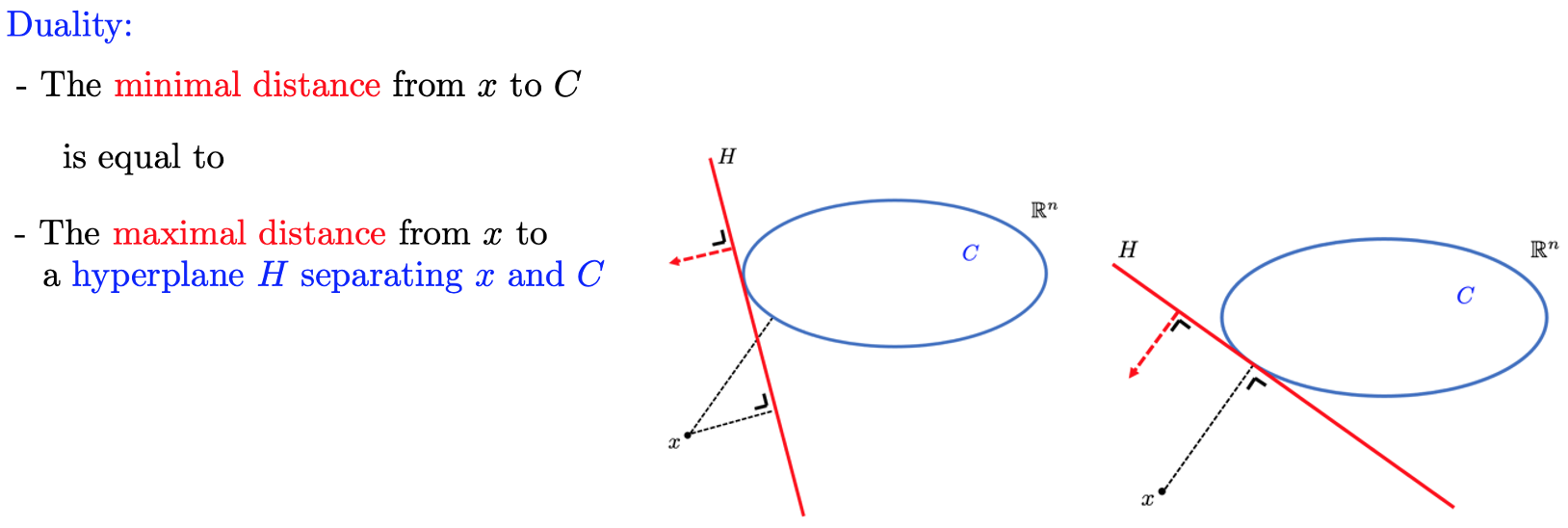
Existence separating hyper-plane

Existence separating hyper-plane

Why does V need to be closed?

Existence separating hyper-plane

Why does V need to be convex?

Supporting Hyper-planes

Relation

Separating hyperplane - Supporting hyperplane

Closure of a set =

smallest closed set that contains the original set = union of the set and all of its limit points

Closed Sets

Property 2.3

Property 2.4

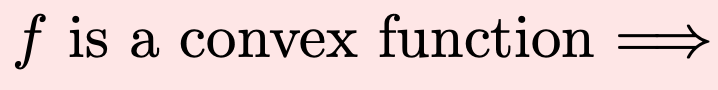
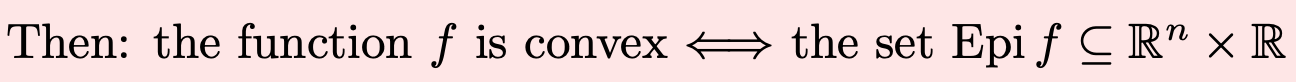
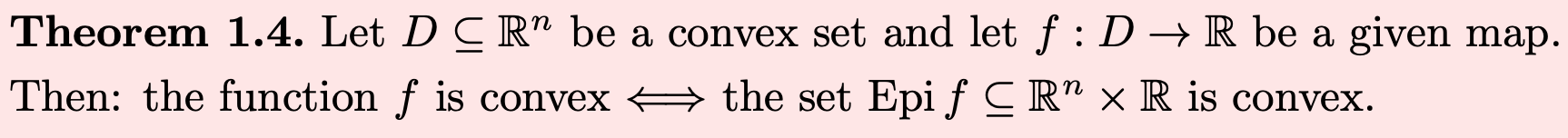
Linear Algebra RECAP

Bounded

Compact

Distance

Half spaces

Definition
Properties

Polyhedral convex set

Convex hull

Theorem 1.5

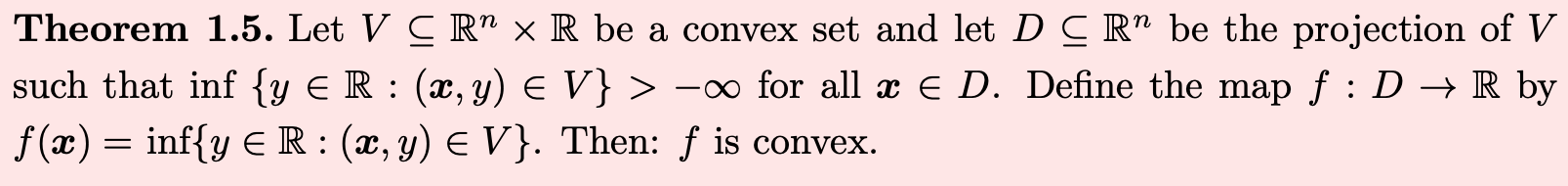
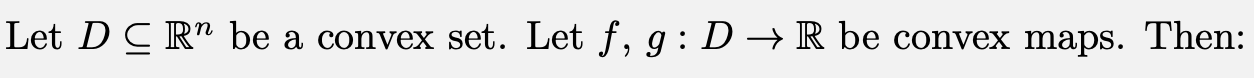
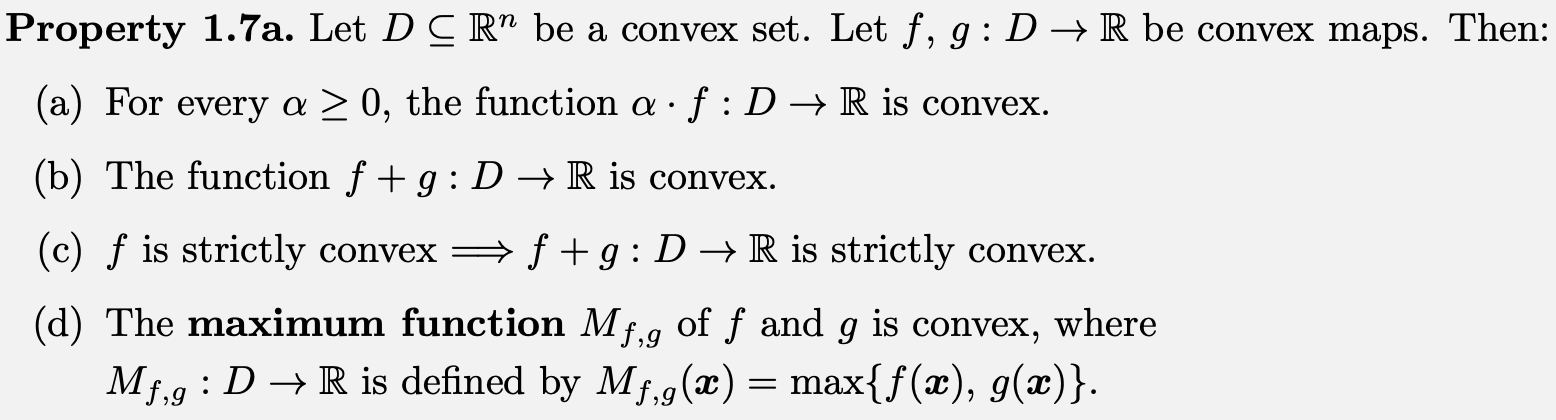
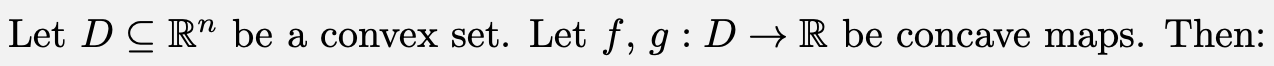
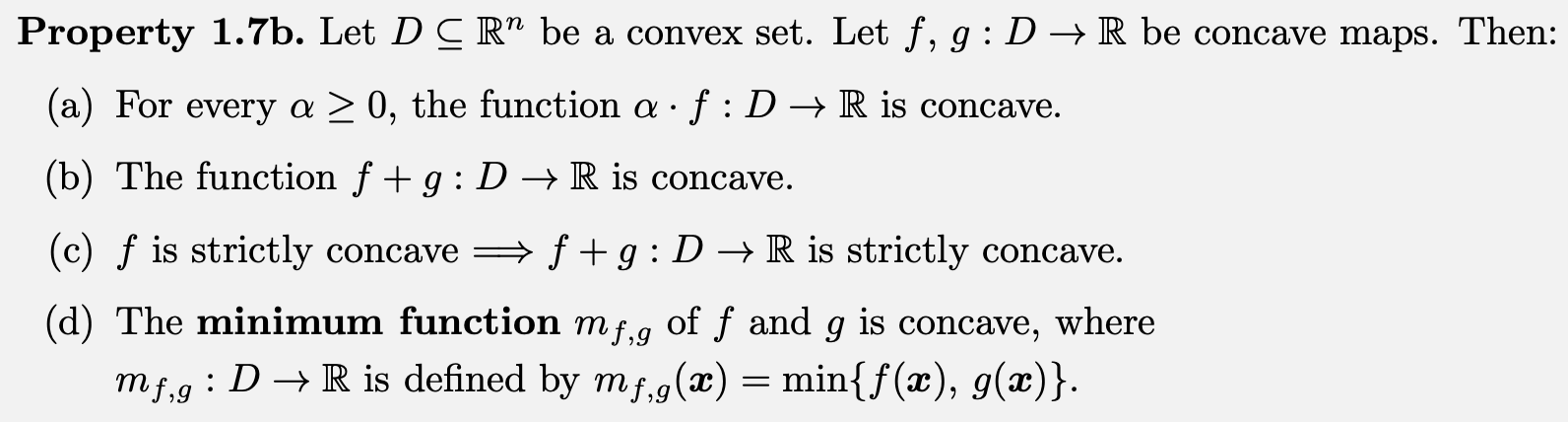
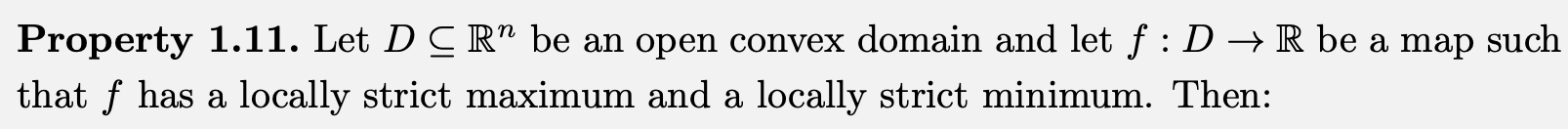
Theorem 1.2