General/PE Handbook

fb (Bending Stress) for typical beam

• fb = M/S

• NDS 3.3

Applied moment for simply supported beam with uniformly distributed load

• M = wl²/8

• Handbook 4.1.7

Elastic Section modulus (Sx) for typical beam

• S = bd²/6

• NDS 3.3

• The elastic section modulus is for serviceability design of non-compact members, used to control deflections

  • Opposite of plastic section modulus which designs for ultimate/collapse

fv (shear stress) for typical beam

• fv = VQ/Ib = 3V/2bd

  • This is just the shear flow divided by the breadth/thickness of the beam

• NDS 3.4.2

ASD Design

• Uses adjustment factors to decrease nominal strength to design strength

  • Won’t be used to factor the applied loads

• Used for wood and masonry design

• Can be used for steel and concrete, HAVE TO FACTOR STRENGTH IF ASKS FOR ALLOWABLE

  • Most commonly will be dividing strength by 2.0 for steel

LRFD Design

• Uses strength reduction factors to decrease nominal strength to design strength AND uses load combinations to increase service loads to ultimate loads

  • If the question asks to factor the applied load then I should definitely use LRFD

• Used for concrete, steel and bridge design

Nominal strength

• Calculated strength of a material before being reduced/factored

• Letter with subscript n for LRFD

• Letter without apostrophe for ASD

Design strength

• Reduced/factored strength of a material using strength reduction/adjustment factors

• Phi next to letter with subscript n for LRFD

• Letter with apostrophe for ASD

Strength Reduction and Adjustment Factors

Factors provided in each codebook to decrease calculated material capacities for factors of safety, used for both ASD and LRFD design

Service Load

• The nominal or unfactored calculated applied load on a member

Ultimate Load

• The increased/factored applied load on a member

• Letter with subscript u for LRFD

• Letter with apostrophe for ASD

Load combinations

A series of load factors found in each codebook that are dependent on loading conditions

Resultant Force for multiple PLs on a beam

• Rf = sum of all forces in a direction

• xR, use sum of moments with only resultant applied force and support reaction forces to find xR

Process to find maximum moment for multiple moving unequal concentrated loads across simply supported beam

• First find support reaction forces through sum of moments

• Determine the applied resultant force by adding up all the applied forces

• Determine the resultant location along the beam through a sum of moments with only the resultant force on the beam and one of the calculated reactions

• Then using maximum moment principle from Handbook 4.1.2 align the resultant and the greatest/middle concentrated load to be equidistant from the beam’s centerline. Choose the load and the side of the load based on what would create the maximum moment. May need to check multiple scenarios

• Redo the support reaction force calculations

• Then find the moment at the location of the applied load close to the centerline by taking a cut/section through the beam at that location and solving

Table with presumptive bearing capacities by soil type

• IBC Chapter 18 - Soils and Foundations, 1806 has presumptive values

Abutment

The retaining wall/foundation wall at the ends of a bridge

Culvert

A tunnel that goes below a road/driveway that’s intended for stormwater drainage

Material unit weights

• ASCE 7 Commentary C3

• AASHTO Table 3.5.1-1 (extremely general)

Ashlar stone

Opposite of rubble stone, this will be very finely cut rectangular stone

Beam under torsion

• Torsion is like wringing a towel out, or rotation along the length of the beam

• Torsion causes shear stresses in the beam

• Circular beams are the strongest against torsion

• Torsional Stress Tau (T) = Torque (T) * r / J (Polar moment of inertia)

  • So the torsional stress increases as the radius/beam size increases

  • And torsional stress decreases as polar moment of inertia increases

  • These occurrences are because like a moment arm, the mass far from the object’s centroid will be much more efficient at resisting torsional stress than mass near the object’s centroid

Polar Moment of Inertia

• Measure of objects resistance to torsion/twisting, like a shaft being turned

• This is the sum of (2) axes of moments of inertia

• J = r² * A

  • r = radius of gyration

Radius of Gyration

• Radius of an area from a point where that area highly affects the moment of inertia

• rx = sqrt(Ix/A)

Moment of Inertia

• Ix = Integral (x²)dA

• An object’s resistance to rotation based on its mass

  • Ix is resistance in rotating about the x axis (deflecting for a beam)

  • Iy is resistance in rotating about the y axis (buckling for a column)

• The x² accounts for the fact that mass further from the centroid has a much higher resistance to rotation than the mass near the centroid

• dA is a tiny slice of the overall area

• Moment of inertia has distance units to the 4th power

• Also known as second moment of area…

Shear Diagram

• Should step vertically at concentrated loads, slope linearly at UDL, and slope parabolically at triangular distributed loads.

• Mmax is typically where the V diagram crosses the x-axis and the shear is zero

• V will have values at start and end of diagram

• Unaffected by hinges or internal moment couples

• V should jump to opposite side of V diagram at all supports

• Capital W = total load on beam, while lowercase w = distributed load per unit length

Moment Diagram

• Should slope linearly where V diagram steps rectangularly, slope parabolically where V diagram slopes linearly, and slope cubically where V diagram slopes parabolically

• Change in section of M diagram = area under section of V diagram

• M will be zero at any hinges

• M will start and end at zero except for at fixed supports where it should have a value

• Should be similar to a deflection diagram in that Moment should be negative for extreme sagging/deflection like at concentrated loads or UDL, and Moment should be positive for hogging/upwards bending

  • An isolated CCW moment at the midspan causes a jump in the M diagram since it would be picking up the right side of the beam/relieving the right side from tension (as represented by the bottom side of the M diagram)

Negative Moment Zone

In beams, typically over intermediate supports and in cantilever beams, where the top edge turns into tension (hogging) and the bottom turns into compression.

Unit weight of water

62.4pcf

Effective soil stress at a certain point

• Effective stress = Total stress - pore water pressure

• Total stress is sum of soil layer unit weights multiplied by the height of each soil layer above the point in question

• Pore water pressure is just water unit weight 62.4pcf multiplied by height of water layer about point in question

Diaphragms

• Floor and roof systems act as deep beams for lateral line loads, so the moment within a diaphragm M = wl²/8

• The structure perimeters that are along the length of the line load are the chords, whose force can be found from taking a cut through the deep beam and using the T/C moment couple along with the beam depth to find the Fc/Ft = M/d

• The structure perimeters that are on the edges of the line load are the struts, whose force can be found from a simply supported beam with a UDL, F = wl/2

• Extra - Next step in lateral force transfer would be dividing strut reactions by wall length to get unit shear

Zero force members in trusses

• All non-collinear members at 2-member and 3-member joints where no external loads are applied

• Then do sum of forces in x and y to check for other zero force members

First moment of area

• Q = A*ybar

• Cross sectional area of the outer member of a composite/built-up member multiplied by ybar (the distance b/t center of entire cross section to center of outer member)

Shear flow

• q = VQ/I

  • Q = first moment of area, see flashcard

• Horizontal distribution of shear force per unit length over a composite/built up cross-section like I-beams used to determine fastener spacing for nails/bolts to prevent the different composite section components from sliding apart

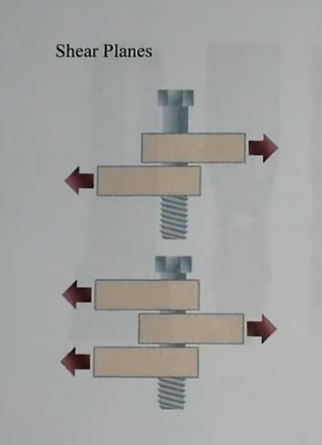
Shear plane

• Failure location for a bolt connecting steel plates

• For several steel plates, the force on the bolt cross section where it will fail will be reduced by the number of steel plates and the increased number of shear planes

Stress and strain, principal stresses

• PE Handbook 1.6.4, Mohr’s circle

• Equation for principal stress

• Note that tensile stresses are positive and compressive stresses are negative

Eccentricity

• e = distance from center

• To calculate eccentric stresses, find the moment induced by the eccentricity (M = F*e), and then the eccentric bending stress induced by the moment (fb = M/S)

  • For the max compressive stress exerted onto a support (typically the foundation), the eccentric bending stress should be added to the normal compressive stress (fc = F/A), just the applied load divided by the area of the transfer member (usually a post or column)

IBC Deflection Limits

• Chapter 16 - Structural Design, 1604 - General requirements, 1604.3 - Serviceability

• For deflection limits, you get out whatever unit you put into it. Put span in inches then you get allowable deflection in inches, and vice versa with feet

Stress

Force divided by an Area

Strain

• epsilon = change in length divided by the original length

• Unitless

• Strain has a direct relationship with ductility

Modulus of Elasticity

• E = stress divided by strain

  • So E = (F/A) / (change in L/original L)

Elastic longitudinal deformation

Delta = PL/AE or play

Relative Density

• Dr is a percentage of how dense/compact the soil is

• Multiple graphs in Handbook to determine or huge equation in transpo section, but table with associated N60 values is the quickest

  • Note that transpo section does have some helpful Geotech stuff

• The void ratio e will be max at Dr = 0% and min at Dr = 100%

Linear Interpolation

• Set slope of 4 known points equal to slope of 3 known points, then solve for the unknown point

• (y2-y1) / (x2-x1) = (y-y1) / (x-x1)

  • Where blank x and y values are the new data set we’re searching for

• Just multiply the left side by (x-x1) and add y1 to solve for y, or solve for x

Process to find total lateral earth force per unit length for retained soil acting on a retaining wall

• Multiply unit weights (dry soil, saturated soil, water, etc.) by Ka (coefficient of active pressure) to get triangular pressures

  • Then multiply by areas to get force per unit length, noting that the soil above the water table will have a triangular pressure above the water table and a rectangular pressure below the water table

• Alternatively you can just find the average soil unit weight (unit weight 1 x height 1 + unit weight 2 x height 2) / total wall height

  • Then use F = .65 * ka * avg unit weight * (total wall height)²

Submerged Soil Density

• This is the density of the soil itself that is under water

• Gamma prime (submerged density) = Gamma saturated - Gamma water

Lateral earth pressure facts

• k coefficients are a ratio of the horizontal stresses divided by the vertical stresses exerted by the soil

• The strain required to achieve passive pressure is much larger than the stress required to achieve active pressure

  • Active pressure is the backfill soil pushing the wall over (0.2<ka<0.4)

  • Passive pressure is the wall sliding into the soil opposite the backfill and compressing the soil (3<kp<10+)

  • At rest pressure, used to design for rigid retaining/foundation walls like basements or bridge abutments (0.4<k0<0.6)

• Active earth pressure can be negative, typically in cohesive soil where the soil is expanding away from the wall causing soil tension cracks