C1: Exam questions [thermal physics in domestic and industrial applications]

Work is done on a box when it is lifted from the floor onto a shelf. Which of these is the same as the work done on the box? (1)

A distance moved by the box

B energy transferred to the box

C force applied to the box

D time taken to move the box

B

The box exerts pressure on the shelf. Identify the unit of pressure. (1)

D

An electric drill has a power output of 0.4 kW. Give the power output of the drill in watts. (1)

400W

A kettle is full of water. The kettle uses 497 000 J of energy to raise the temperature of the water from 20 °C to 100 °C.

Show that the mass of water in the kettle is approximately 1.5 kg. Use the equation Q = mc∆T Specific heat capacity of water = 4200 J kg-1 °C-1 Show your working. (3)

substitution (1) 497 000 = m x 4 200 x (100-20)

rearrangement (1) m = 497 000 4 200 x 80

evaluation (1) 1.479(kg)

The kettle does not switch off when the water starts to boil. The kettle continues supplying thermal energy until all 1.5 kg of water has boiled away at the same temperature of 100 °C.

Calculate the amount of energy needed to vapourise 1.5 kg of water in the kettle. Use the equation Q = ΔmL Specific latent heat of vapourisation of water is 2.26 x 106 J kg-1 Show your working. (2)

substitution (1) E = 1.5 x 2.26 x 106

evaluation (1) 3.39 x106 (J)

A technician heats a metal plate made from cast iron. After a few minutes the temperature of the metal plate is constant when it reaches thermal equilibrium. Describe what is meant by the term thermal equilibrium. (2)

there is no net (thermal) heat transfer/input energy is balanced by the output energy (1)

energy flows/transfers in (from the heat source) and out of the metal plate (to the surroundings) (1)

The cast iron plate has a high thermal capacity. Describe what is meant by the term thermal capacity. (2)

the amount of thermal energy (added to the metal plate) (1)

which gives {a rise/change in temperature of 1K/unit temperature rise/change} (1)

State the law of conservation of energy. (1)

the total energy (of an isolated system) remains constant/is conserved (1)

energy cannot be {created/made} or {destroyed/lost} (1)

The first law of thermodynamics can be stated as Q = ∆U + W

State what is meant by the term W. (1)

work (done by the system)

A student uses the foot pump shown in Figure 2 to inflate a bicycle tyre.

The temperature of the air in the barrel increases as the tyre is pumped up. The friction in the pump is negligible. Explain why the temperature of the air in the barrel increases. (4)

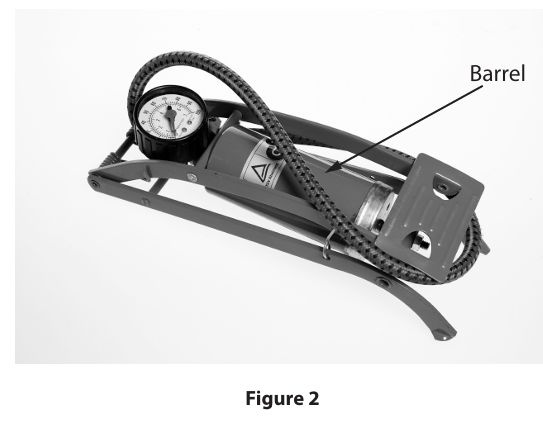
(the) air is compressed (1)

(when the user of the pump pushes down on the pump) the volume decreases (1)

(so) air pressure increases (1)

AND work is done on the gas (1)

(so, the) particles/molecules /air gain/increase kinetic energy (from the moving piston) (1)

The barrel of the pump has a volume of 3.8 x10-4 m3. The temperature of the air in the pump is 303 K and exerts a pressure of 2.5 x 10⁵ Pa on the walls of the pump.

Calculate, using the ideal gas equation, the number of molecules of air that are present in the barrel of the pump. Boltzmann constant k = 1.38 × 10^-23 m2 kg s^-2 K^-1 Show your working. (3)

substitution (1) 2.5 x 105 x 3.8 x10-4 = n x 1.38 × 10-23 x 303 rearrangement (1) N = 2.5 x 105 x 3.8 x10-4 1.38 × 10-23 x 303 evaluation (1) 2.27 x 1022 (molecules)

A piston in an engine compresses gas in a cylinder and heats the gas. The piston does work on the gas. Work done can be calculated using the equation W = F∆x Identify what F stands for. (1)

A fatigue

B fluid

C force

D fusion

C force

Give the meaning of the terms in the equation. (2)

Δ= ??

x= ??

Δ=change in

x= distance/diplacement

Which is the correct unit for thermal capacity? (1)

A J kg K

B J K

C J K^-1

D J kg^-1 K^-1

C J K^-1

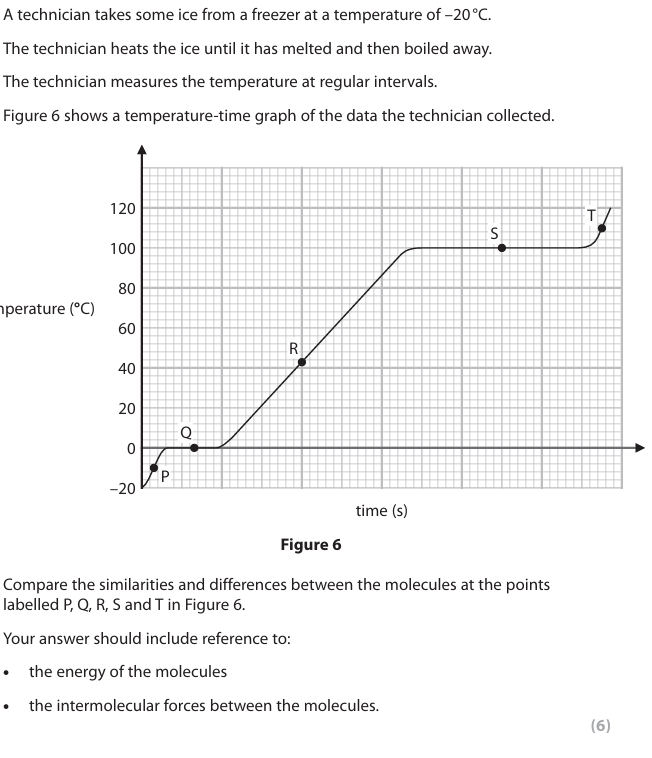
Explain how the motion and arrangement of the molecules in the ice cube change as it melts. (4)

molecules move faster/more freely (1)

expansion because they have{gained/absorbed} energy (from surroundings) (1)

and identification arrangement of molecules goes from {fixed/regular position} to more {random /irregular/moving from place to place} (1)

expansion because the intermolecular forces are weakened (1)

Steam engines are a type of heat engine. The steam expands adiabatically in part of a steam engine. Which one of these statements is correct for steam expanding adiabatically? (1)

A There is a change in temperature.

B There is a change in the number of molecules.

C There is no change in pressure.

D There is no change in volume

A There is a change in temperature.

The steam engine obeys the second law of thermodynamics. Explain how the steam engine obeys the second law. (2)

identification not all the heat energy can be converted into work/useful energy/not 100% efficient (1)

expansion as some of the energy must be lost to the {environment/surroundings} (1)

Describe how a steam engine is an example of a heat engine. (3)

(a system that) converts/changes/transfers {thermal or heat/chemical/stored energy} (1)

into mechanical energy/{movement/kinetic} energy (1)

to do (useful) work (1)

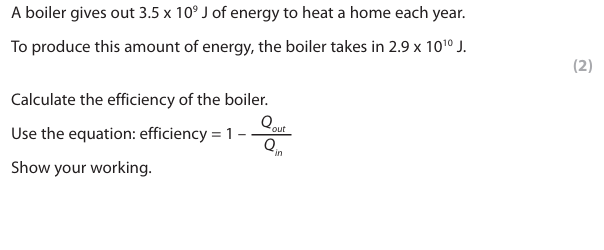
Give a value for an amount of energy that the boiler should take in to increase its efficiency. (1)

any value more than 2.9 x 10¹⁰ (J)

Which energy store has increased for the bricks on the roof compared to when the bricks were on the ground? (1)

A elastic potential

B electrical

C gravitational potential

D kinetic

C (gravitational potential)

Which unit measures the power of the electric motor in the crane? (1)

A joule

B newton

C pascal

D watt

D (watt)

The electric motor is not 100% efficient. Explain why the efficiency of the electric motor is less than 100%. (2)

some energy is {wasted/lost/dissipated/given off/released} (1)

(because it is) transferred to {thermal/heat/surroundings/environment/ motor} (1)

(because it is doing work against) friction (1)

Steam at a high temperature is compressed in a cylinder by a piston. Which statement is correct for the steam during compression? (1)

A The kinetic energy of the steam molecules increases.

B The mass of steam increases.

C The density of the steam decreases.

D The number of molecular collisions stays constant.

A

The steam is at a pressure of 4.5 x 105 Pa. The volume of the cylinder changes by 0.3 m3. Calculate the work done on the steam by the piston. Assume the steam pressure remains constant. Use the equation: W = p∆V Show your working. (2)

135 000 (J)

Which type of energy is the sum of all the energy of the steam molecules? (1)

A internal

B kinetic

C potential

D elastic

A

A kettle of water is boiled next to a window. Condensation forms on the window when the steam changes into water droplets. The window is at room temperature. Describe the behaviour of the water molecules as the steam condenses to form water droplets on the window. (4)

(Before contact with window) steam {molecules/particles} are {far apart/moving freely/moving fast} (1) (Contact with the window) (when the steam comes into contact with the window it) water molecules/particles {lose (kinetic) energy/move more slowly} (1) move closer together (1) (After contact with window) (steam changes) from vapour to liquid (1)

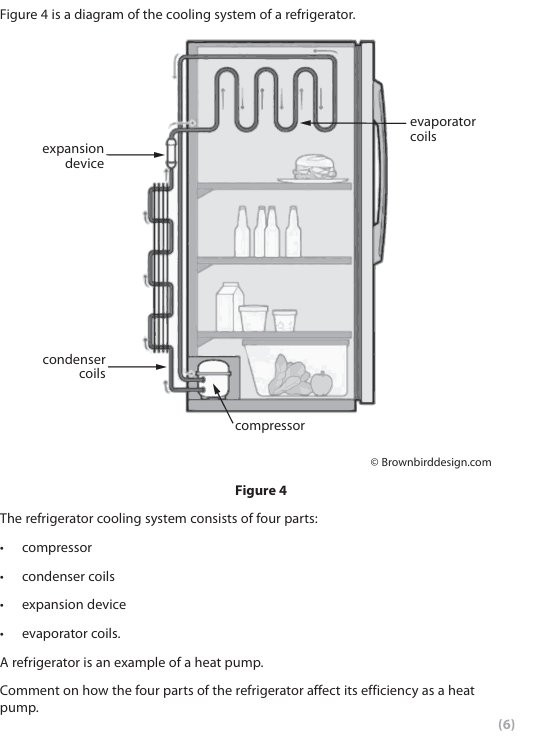
A refrigerator is a type of heat pump. The contents of a refrigerator are kept at a temperature of 6°C. (a) Give this temperature in Kelvin (K). (1)

(6 + 273) 279.15 (K)

fds

gd

The first law of thermodynamics can be written as an equation, Q = ∆U + W. (a) (i) Give the meaning of the letter Q in the equation. (1)

energy supplied/transferred

A cylinder of helium gas is used to inflate a balloon. The helium gas expands into the balloon. Explain why the temperature of the helium gas does not change if the balloon is inflated slowly. (2)

Identification (slowly filling the balloon) needs time for energy transfer from the surroundings to the helium gas (1) OR to reach thermal equilibrium between the surroundings and the helium gas (1) Expansion so the expansion is isothermal(1)

A sealed cylinder contains helium gas. The cylinder containing the helium gas is heated. The cylinder has fixed dimensions. (i) Which quantity increases for the helium atoms, when the cylinder is heated? (1)

A average density of the atoms

B average kinetic energy of the atoms

C total number of atoms

D volume of each atom

B

gf

part E {no change/constant} (in pressure) (1) part F (pressure) {increases/rises} (1) part G {rapid/sharp/great} increase (in pressure) (1) part H (pressure) {decreases/falls/drops} (rapidly) (1)

vf

fds

An electric heater is used to heat some water in a shower. (i) The heater produces 5000 joules of energy every second. Water enters the heater at a temperature of 289 K. The mass of water flowing through the heater every second is 0.08 kg. Calculate the temperature of the water leaving the shower.

Specific heat capacity of water = 4200 J kg^{–1 K–1} (4)

substitution (1)

5000 = 0.08 x 4200 x (T – 289) OR

5000 = 0.08 x 4200 x ΔT rearrangement (1) (T – 289) = 5000/0.08 x 4200

304K

The temperature of the water leaving the shower is measured to be different from the calculated value. Explain why the temperature is different. (2)

Identification- the water temperature will be lower (1)

Expansion- (because) energy is transferred or {lost/ wasted} to the surroundings (1)

Which temperature is 2 °C in kelvin? (1)

275

Explain the function of the condenser in Figure 1. (2)

removes /transfers{(thermal) energy/heat} from the refrigerant/to the surrounding (1)

changes or turns the gas into a liquid

fsd

substitution (1) 5 x 105 = m x 4200 x 80

rearrangement (1) (m =) 5 x 10⁵ / 4200 x 80

evaluation (1) 1.5 (kg)

The water in the pan boils and forms steam. Explain what happens to the intermolecular structure when water forms steam. Your answer should refer to intermolecular forces and intermolecular spacing. (4)

molecules close together/in contact (in liquid) (1) so, there are (stronger) forces between the molecules (in the water) (1)

the particles (in water) gain energy (1) (when heated the molecules) are able to separate/move apart (in gas) (1)

there are (almost) no forces between the molecules (in the steam) (1)

Which is the correct unit for specific latent heat of vapourisation? (1)

A J K⁻¹

B J kg⁻¹

C J K⁻¹ s⁻¹

D J kg⁻¹ s⁻¹

B

volume difference of ∆V (1) 6.0 x 10-4 – 1.0 x 10-4

substitution (1) 205 000 x 5 x10-4

evaluation (1) 102.5 (J)

A petrol engine is an example of a heat engine. Describe what a heat engine does. (2)

transfer/convert thermal energy (1) into kinetic energy/ mechanical/ does work (1)

In ideal engines, adiabatic and isothermal expansions are reversible and the first law of thermodynamics, ΔU = Q − W, can be applied. Complete the sentences in Paragraph 1 to give ΔU for each type of expansion. (2)

In an adiabatic expansion, ΔU = ................................................................................ .

In an isothermal expansion, ΔU = ..................................................................................

In an adiabatic expansion, ∆U = (-) W (1)

In an isothermal expansion, ∆U = 0 or zero (1)

Discuss, using Figure 5 and Table 1, the efficiency of an ideal engine cycle and that of the petrol engine cycle. You may add a diagram of the ideal engine cycle to support your answer. (6)

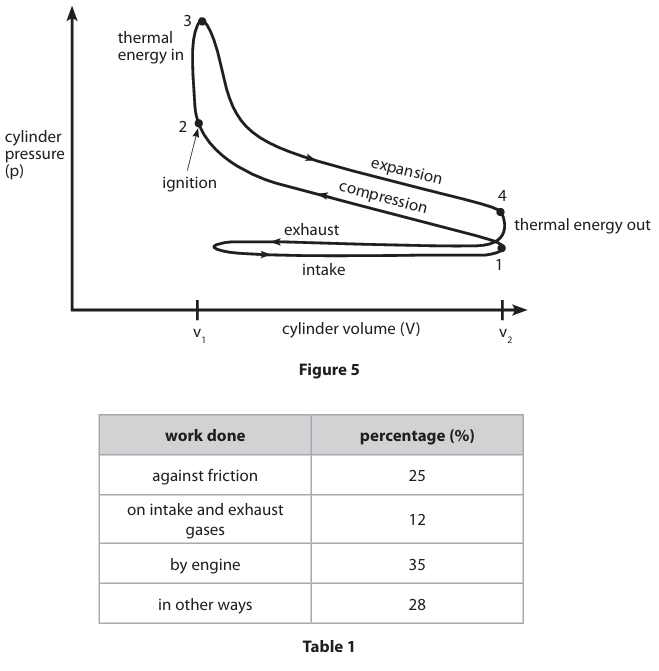
vds

Give the value of 45 kW in watts. (1)

45 000 (W)

The lifts in the building rise through a height of 0.5 km. The weight of one lift cabin is 12 500 N.

Show that the motor does approximately 6 000 000 J of work raising the lift cabin 0.5 km. Use the equation: W = FΔ x (3)

conversion (1) 0.5 km = 500m substitution

(1) W = 12 500 x 500

evaluation (1) 6 250 000 (J)

The efficiency of the lift motor is 0.85. Calculate the work input to the motor when raising the lift cabin. If you did not get an answer for (b)(i), use the value 6 000 000 J for the work output. (3)

Use the equation efficiency = useful energy output/ total energy input

Two beakers contain olive oil at the same temperature. The first beaker contains 1 kg of olive oil. The second beaker contains 0.5 kg of olive oil. (a) (i) Which physical property is different for the olive oil in each beaker? (1)

A average density

B kinetic energy

C molecular separation

D thermal capacity

D

A thermometer is used to measure the temperature of the olive oil in a beaker. The thermometer is left in the olive oil for a few minutes until the olive oil and the thermometer reach the same temperature. Explain why the thermometer and the olive oil are now at the same temperature. (2)

(the olive oil and the thermometer have reached) thermal equilibrium (1) AND because there is no net energy transfer (between the two) (1)

OR (thermal) energy transfer from thermometer to liquid equals (thermal) energy transfer from liquid to thermometer (1)

A learner fills a container with some olive oil at room temperature. The learner then places the container of olive oil in a freezer. A few hours later the olive oil has frozen solid. Describe the motion and arrangement of the molecules in the olive oil before freezing and after freezing. (4)

Before freezing:

molecules moving {randomly/sliding over/ around} each other (1) {irregular/random} arrangement (1) weak(er) forces/bonds between the molecules (1)

After freezing:

molecules are in fixed positions/only vibrate (1) {tightly/closely} packed OR regular {arrangement/lattice} (1) molecules closer together/smaller spacing between molecules (1) strong(er) forces/bonds between the molecules (1)

fds

Which statement correctly describes the internal energy of a system? (1)

A The kinetic energy of the molecules only.

B The potential energy of the molecules only.

C The sum of the potential energy and kinetic energy of the molecules.

D The difference between the potential energy and the kinetic energy of the molecules.

C

Complete Sentence 1 to define the second law of thermodynamics. When an energy transfer takes place in a system, the .................................................................. of the system increases. (1)

entropy

Explain why the pressure changes when the piston moves slowly to the right. Your answer should refer to molecules in the trapped air. (2)

pressure {decreases/reduces/lowers/less} (1) as the air molecules will produce {less frequent collisions/collide less often} with the walls of the cylinder (1)

gfd

A power station generates electrical energy. A turbine in the power station is a heat engine. (a) Describe what a heat engine does. (2)

transfers {thermal energy/heat energy} (in the water/steam) (1) into {kinetic energy/work} (in the turbine) (1)

Steam enters two identical turbines at the same temperature. The temperature of the steam leaving turbine A is lower than the temperature of the steam leaving turbine B. Explain the advantage of using turbine A rather than turbine B. (2)

Identification

Turbine A is more efficient (1)

Expansion

more (of the input) energy is converted into useful work/energy output (1) OR less energy is being lost/dissipated to the environment/elsewhere (1)

fsd

A learner observes that a puddle of water slowly disappears when heated by the Sun on a warm day. (i) Name the process that makes the puddle disappear. (1)

evaporation

Describe how the puddle disappears. Your answer should refer to molecules of water. (2)

water molecules {gain (kinetic) energy/ move faster} (by heating from the sun) (1) molecules at the surface escape from the puddle (1)

Explain why the temperature of the water stays at 100 °C when changing from water into steam. (2)

(all) energy goes into increasing PE of the molecules (1)

moving the molecules apart / breaking bonds between (water) molecules / breaking intermolecular / hydrogen bonds} (1)

(supplied) energy does not go into increasing the KE (of the molecules) (1)

Complete Sentence 1 about the internal energy of the air. (2)

The internal energy of the air is the total amount of ............................................................................................. energy and ............................................................................................. energy of all the air particles in the pump cylinder.

Kinetic / kinetic energy /KE (1)

Potential/ potential energy / PE (1)

Complete Table 1 by circling increases, remains the same or decreases in each box. The first row has been completed for you. (2)

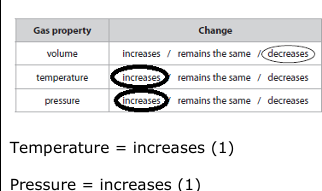
The foot pump in Figure 4 is used to inflate the tyre. The change in volume (ΔV) of air in the pump cylinder is 0.001 m3 . The amount of work done (W) in compressing the air is 101.3 J.

Show that the average pressure (p) of the air in the pump cylinder is approximately 100 000 Pa. Use the equation: W = pΔV (3)

Substitution (1) 101.3 = p x 0.001

Rearrangement (1) p = 101.3 / 0.001

Evaluation (1) 101300 (Pa)

The unit of pressure is the pascal (Pa). (a) Which one of these units is an equivalent to a pascal (Pa)?

A N kg–1

B N m

C N m–2

D N s

C N m–2

The air in an aircraft cabin has a volume of 70.0 m³. The density of air is 1.28 kg m^–3. (i) Calculate the mass of the air in the aircraft cabin. Show your working. (1)

The passengers in the aircraft cabin complain that the cabin temperature is too cold. A flight attendant increases the cabin air temperature. Explain, in terms of molecules in the air, what happens to the pressure in the aircraft cabin when the air temperature increases.

Pressure increases (1)

Air molecules {gain/increase/have more} {kinetic energy /KE} (1) air molecules have a greater speed/velocity (1)

(air molecules) {collide/hit} with the aircraft walls (1)

with{more force/harder/more frequent/more often} with the walls (1)

fd#

In a real example, the working COP is lower than the maximum theoretical value. Explain why. (2)

The heat pump is not 100% efficient (1) Energy is needed to work the {pump/compressor/device} (1) Energy is lost {to the surroundings/to friction/turbulence} (1)

Compare how the heat pump keeps the house cool in summer and warm in winter. (6)

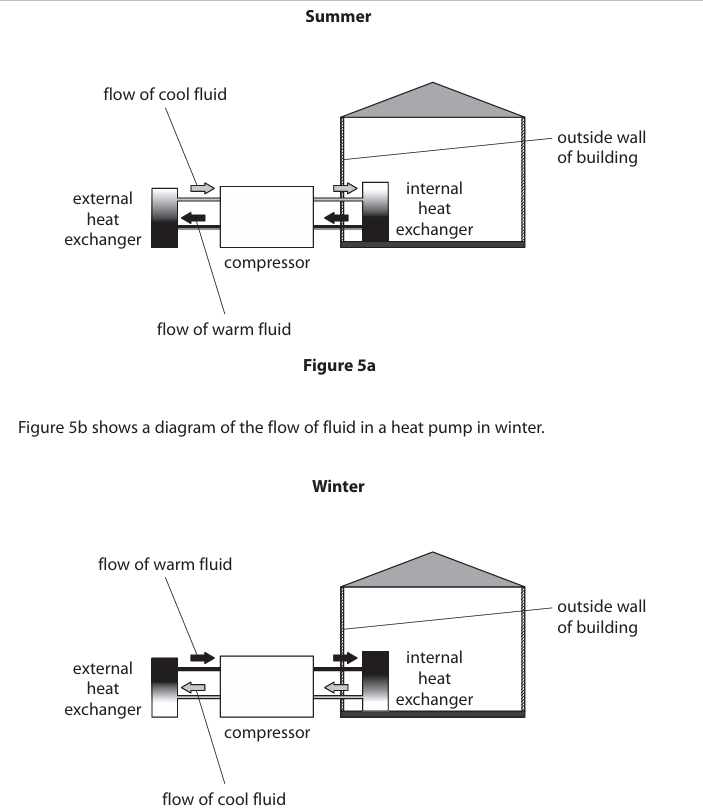
Similarities between summer and winter

-Both cooling and heating are reversible processes depending on the temperature of the surroundings compared to the interior of the building

-Both transfer heat from one place to another

-Both require as large a temperature difference as possible to operate efficiently

-Both rely at some point in their cycle on an adiabatic process

Differences between summer and winter

-The condenser and evaporator work in opposite directions in winter compared to in summer

-In winter, the external heat exchanger draws in heat from the outside of the house and releases it through the internal heat exchanger into the house

-In summer, the external heat exchanger gives out heat from inside of the house to the outside of the house

- In winter, the liquid in the pipes of the external heat exchanger evaporates and turns into a gas, which is compressed and heats up

-In summer, the high air temperature inside the building heats the liquid in the pipes of the internal heat exchanger turning it to a gas

Which one of these is equal to the work done on the weights by the student? (1)

A the efficiency of the exercise

B the energy gained by the weights

C the gravitational force on the weights

D the power output of the student

b

The student in Figure 2 uses a force of 600 N to lift the weights. The weights are lifted from the floor to a height of 0.75 m. Calculate the work done in lifting the weights. Use the equation: W = F × Δ x (2)

substitution (1) W = 600 x 0.75

Evaluation (1) W = 450 (J)

Explain why the amount of work done by the student is different from the amount of work done on the weights. (2)

the amount of work by the student is greater/higher/more (1) (energy) to produce (excess) heat(1) (energy) needed for heart beating faster/ increased blood flow/breathing faster /producing sweat /any valid biological process (1) energy used to {lift (his) own body parts/move muscles} (1) muscles/exercise not 100% efficient (1) energy is {transferred/wasted or lost} to the surroundings (1)

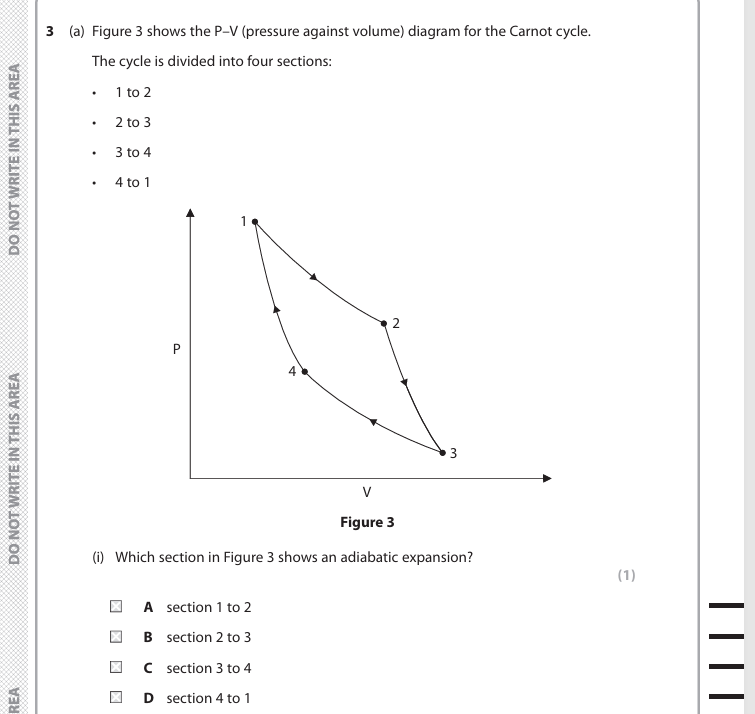
B

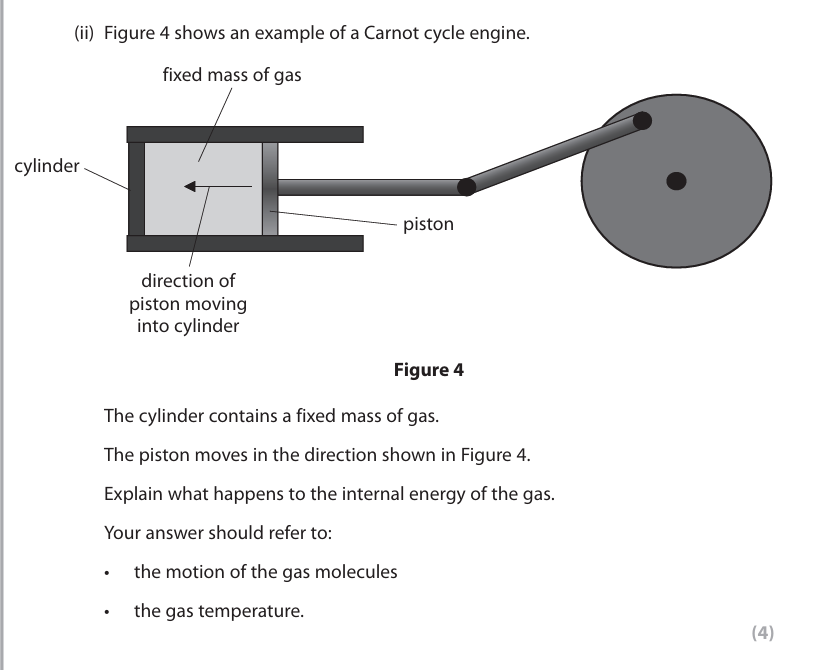
the internal energy increases (1) the gas is compressed / volume decreases / work is done by piston on gas (1) the temperature of the gas increases (1) the molecules move faster / gain Kinetic Energy/KE (1)

A student measures the temperature of some oil in a beaker. The temperature of the oil is 20 °C. (i) Give this temperature in kelvin (K). (1)

293(.15) (K)

conversion of 600g to kg (1) 0.6 (kg) finding the temperature change (1) 50 (K) substitution (1) energy supplied = 0.6 × 2090 × 50 evaluation (1) 62 700 (J)

A solid metal is heated until it melts. The heating continues until the liquid metal boils. Compare the similarities and differences between melting and boiling for a metal. Your answer must refer to:

• the energy of the metal

• the separation between the atoms of a metal

• the forces between the atoms of a metal. You may include an annotated graph and/or diagram to support your answer. (6)