linear algebra

exam review

find rank, compare to the # of variables, if rank is less than the number of variables, then infinite sols

check the det, if its 0 then infinite sols

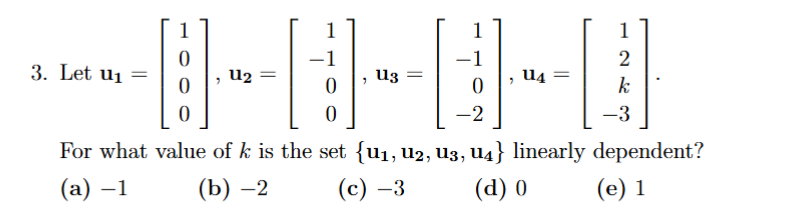
matrix, find the determinant, then see what you need to do to get it to det = 0 to make it linearly dependent since det0 means dependent

get det with k, see what you need to set k for 0 det (recall det = 0 is dependent)

matrix, ref, for consist, set k such that [000|0]

set each one into a matrix, get to ref if needed, then check for consistency by looking for [000|0]

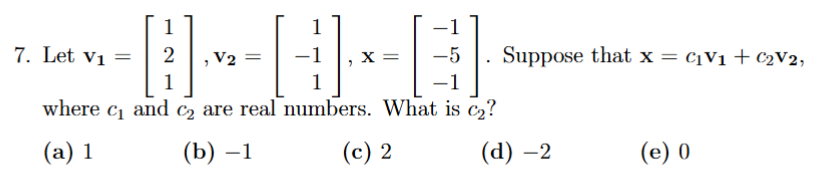
setup c1v1+c2v2 = x, sys of eqs, solve for c2 by subbing

(ad-bc)

cofactor or cross method

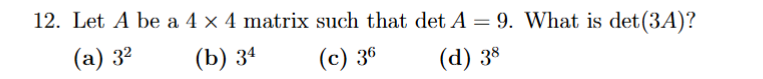
when det(k3) = k^n times the (det), where n is the # of rows/cols

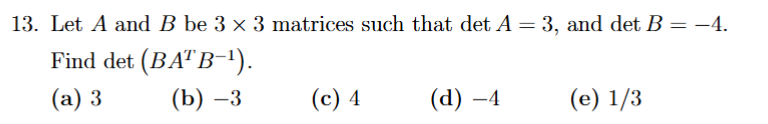
A^t is the same as normal, B^-1 is 1/det

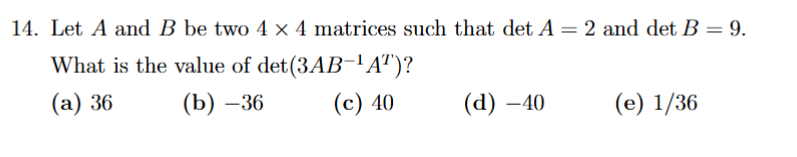
scalar operation is last, transpose same, inverse is 1/det

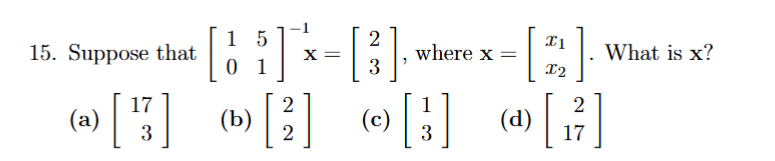
get it to Ax=b by removing the inverse, then sys of eqs, then solve for each x1 and x2.

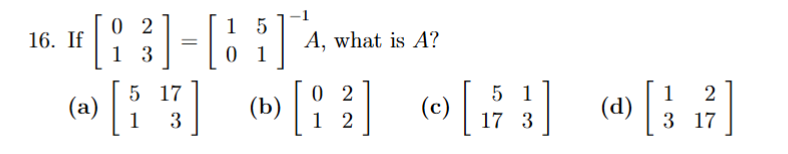
isolate for A.

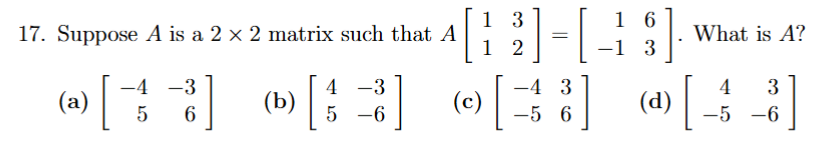
inverse and move past over to isolate A, then multiply to get A

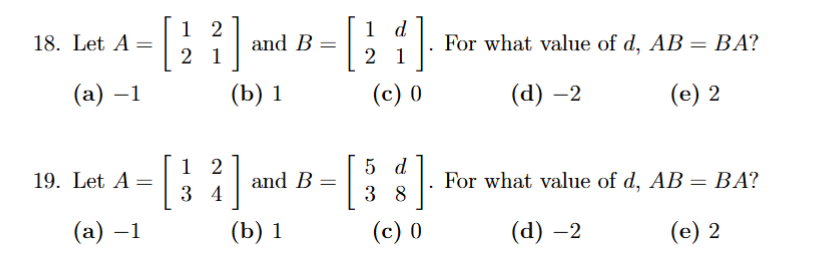
solve AB and BA, then check each corner and isolate

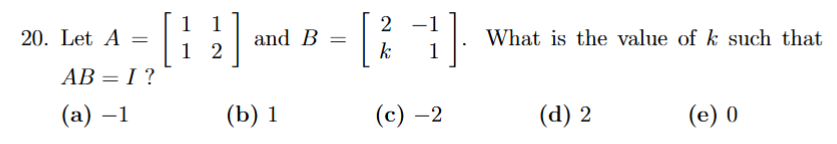
solve AB, then sys of eqs, then corner check and isolate for k

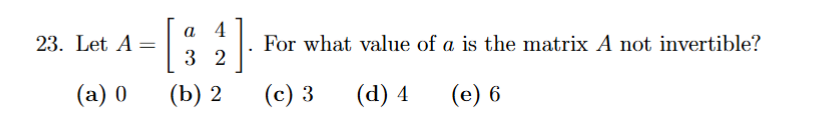
sub in every value and check with det(2×2) for 0

matrix, ref, dimension = # of vars - rank (# of pivs in ref)

number of cols - rank (# of pivots in ref)

sub in given values and isolate

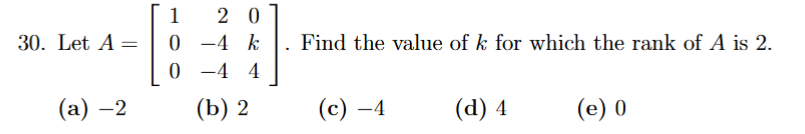
test the values to see how you can remove one row only to get 2 rows in ref

setup A-(λ)(I), get rank in ref, get dimension (cols - rank)

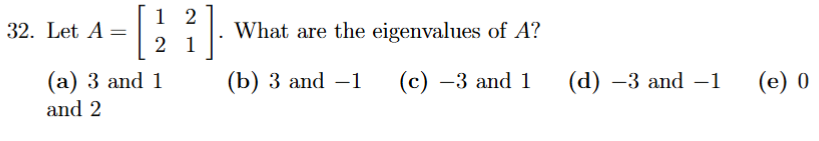
λ² - (a+d)λ+det = 0 , then apply quadratic formula

| z | = √a²+b²

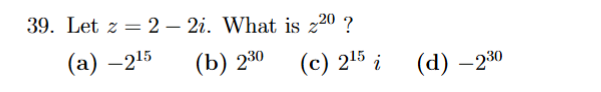
solve using | z | = √a²+b², then apply exp, then compare

multiply across and (2x-1)+(-1x-1) and so forth

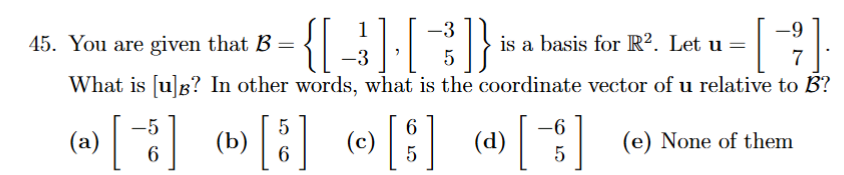
setup ab1 + bb2 = u, sys of eqs, isolate for a and b

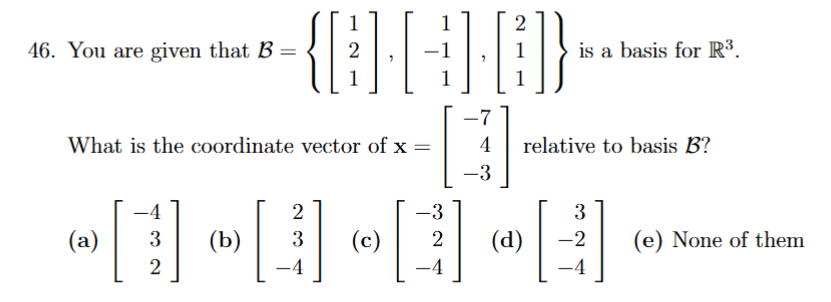
setup ab1 + bb2 = u, sys of eqs, isolate for a and b

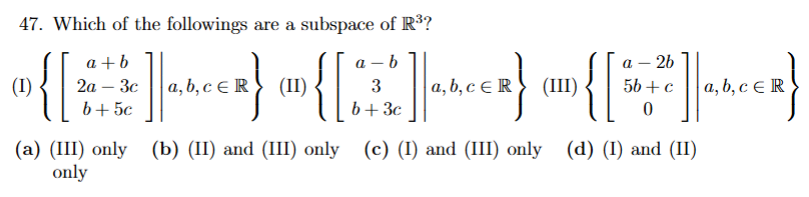
if constant, not in subspace

dot product each possible with the 2 vectors, need 0,0