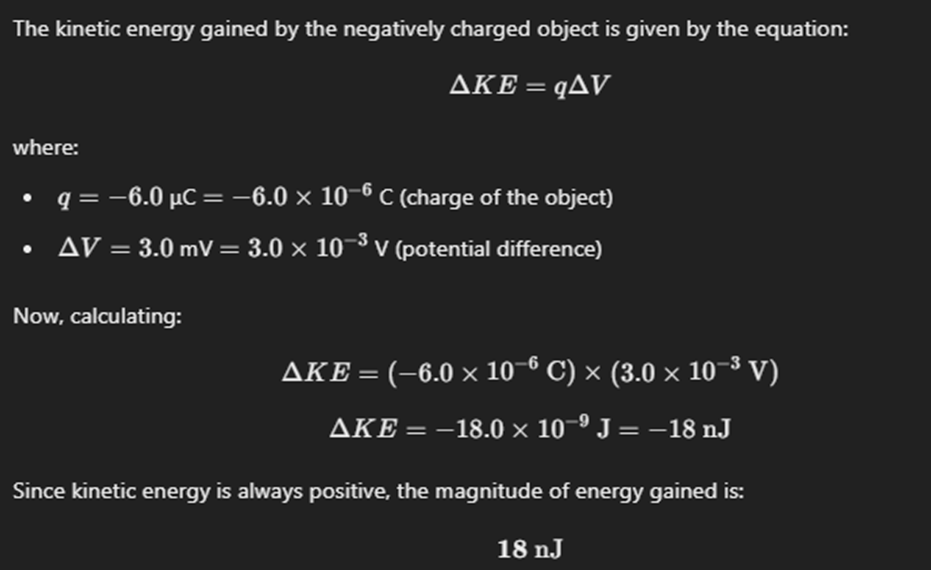Electric Potential and Energy Concepts in Physics
Studied by 0 people
Learn
Practice Test
Spaced Repetition
Match
FlashcardsGravitational Potential Energy
Energy due to mass m at height h.
Electric Potential Energy
Energy due to charge q in electric field E.
1/92
There's no tags or description
Looks like no tags are added yet.
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
93 Terms
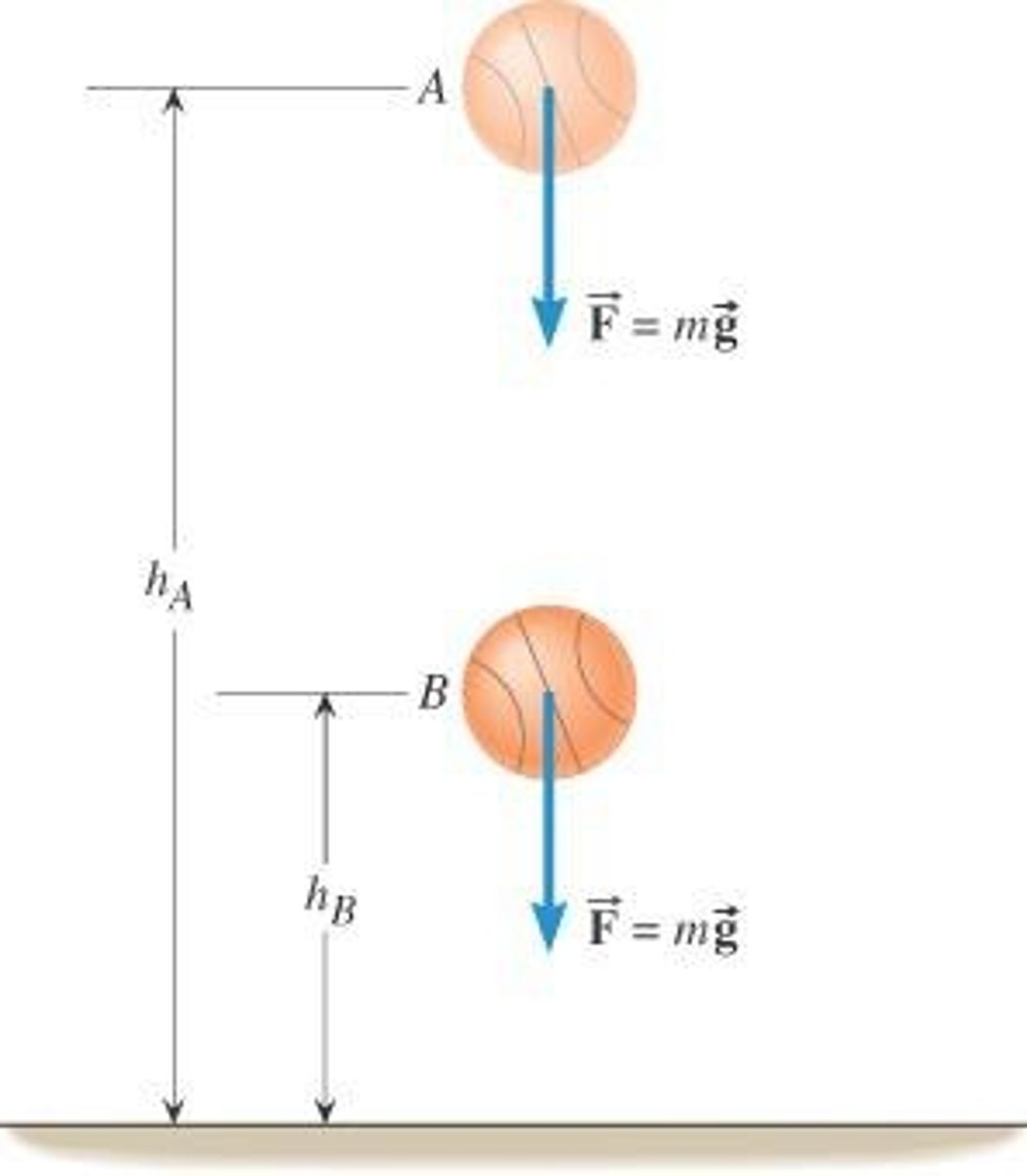
Gravitational Potential Energy
Energy due to mass m at height h.
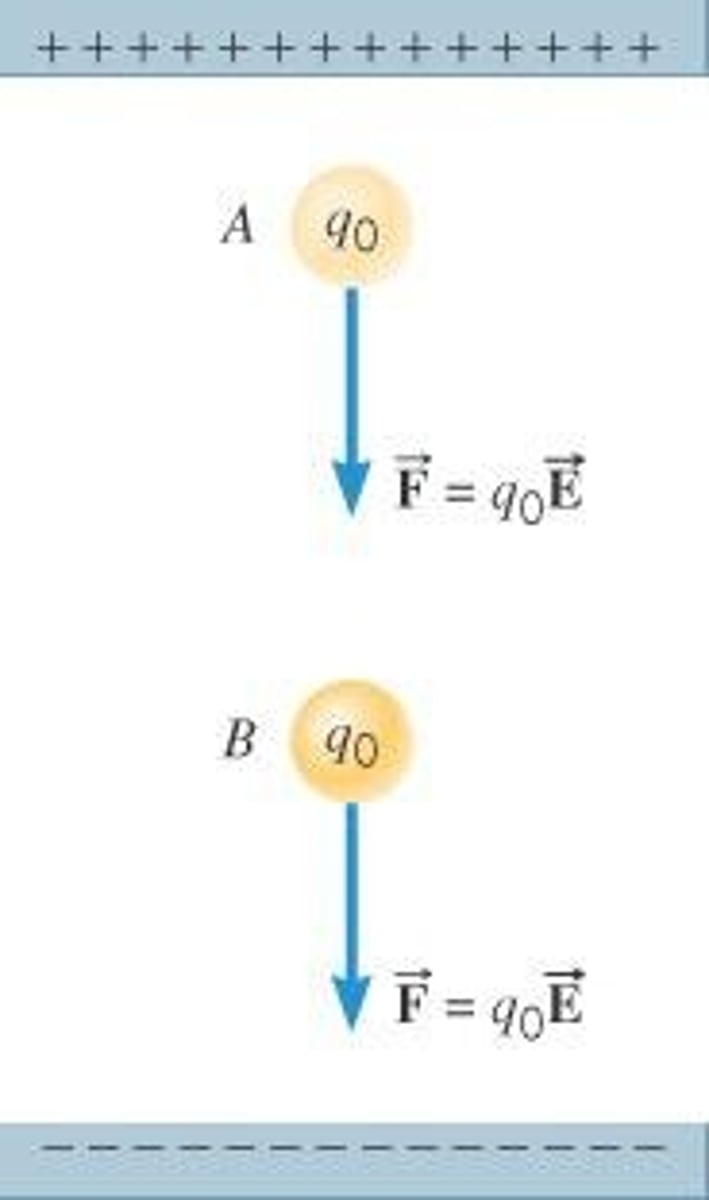
Electric Potential Energy
Energy due to charge q in electric field E.
Electric Potential
Potential energy per unit charge, measured in volts.
SI Unit of Electric Potential
Measured in joules per coulomb (J/C).
Electric Potential Difference
Difference in electric potential between two points.
Work Done by Electric Field
Work done on charge moving in electric field.
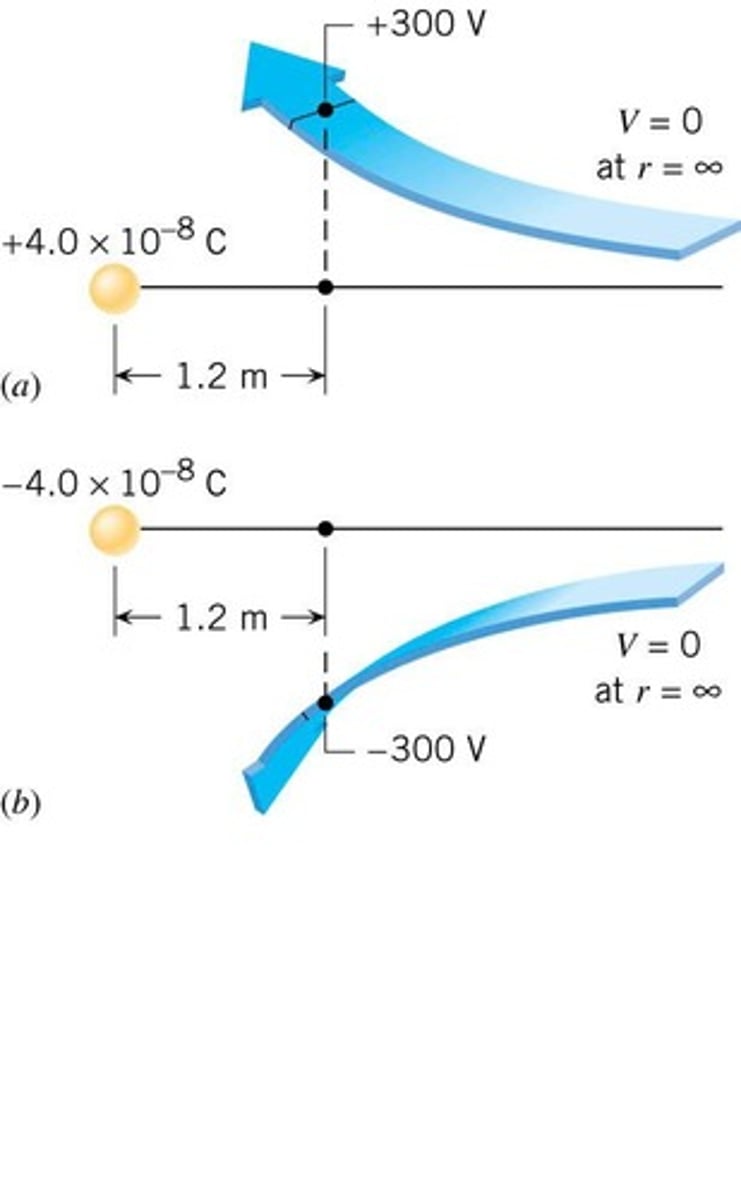
Positive Charge Movement
Moves from high to low electric potential.
Negative Charge Movement
Moves from low to high electric potential.
Electrostatic Force
Conservative force with zero work in closed paths.
Total Energy Conservation
Total energy in isolated systems remains constant.
Potential Energy Formula (Gravitational)
U = mgh, where g is gravity.
Potential Energy Formula (Electric)
U = qEh, where E is electric field strength.
Force due to Gravity
F = mg, where m is mass.
Force due to Electric Field
F = qE, where q is charge.
Work Done by Applied Force
Work equals change in potential energy.
Electric Potential Energy in Total Energy
Includes kinetic, gravitational, and electric potential energy.
Charge on Sphere Calculation
Find charge using mass, height, and speed.
Electric Field Strength
E = F/q, force per unit charge.
Potential Difference Calculation
Integrate electric field over path between points.
Electric Potential Unit Conversion
1 eV = 1.6×10^-19 J.
Work Done by Electric Field Example
Work can be positive or negative depending on charge.
Proton Movement in Electric Field
Potential energy decreases as proton moves to lower potential.
Electron Movement in Electric Field
Potential energy increases as electron moves to higher potential.
Force Variation with Distance
Electrostatic force changes as distance between charges varies.
Mass of Sphere Example
0.20 kg sphere released from 1.0 m height.
Speed of Sphere at Ground
Sphere reaches ground at 1.5 m/s.
Differential Work
Work done by a force over a small distance.
Line Integral
Integral calculating work along a path between points.
Electric Potential (V)
Potential energy per unit charge in an electric field.
Electric Field (E)
Force per unit charge experienced by a test charge.
Reference Point (Vi)
Chosen point for measuring electric potential, often zero.
Electric Potential Energy (U)
Energy stored due to position in an electric field.
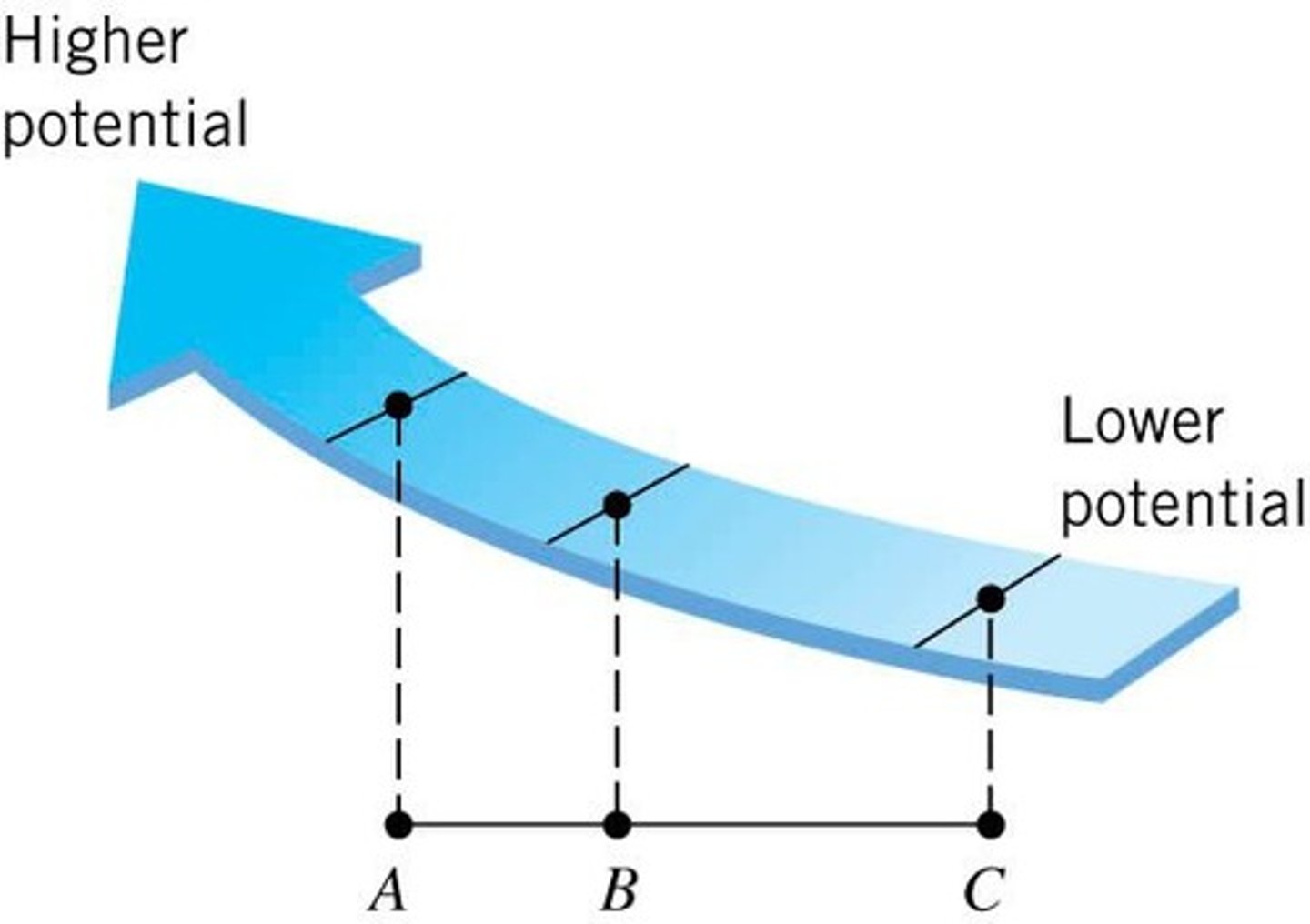
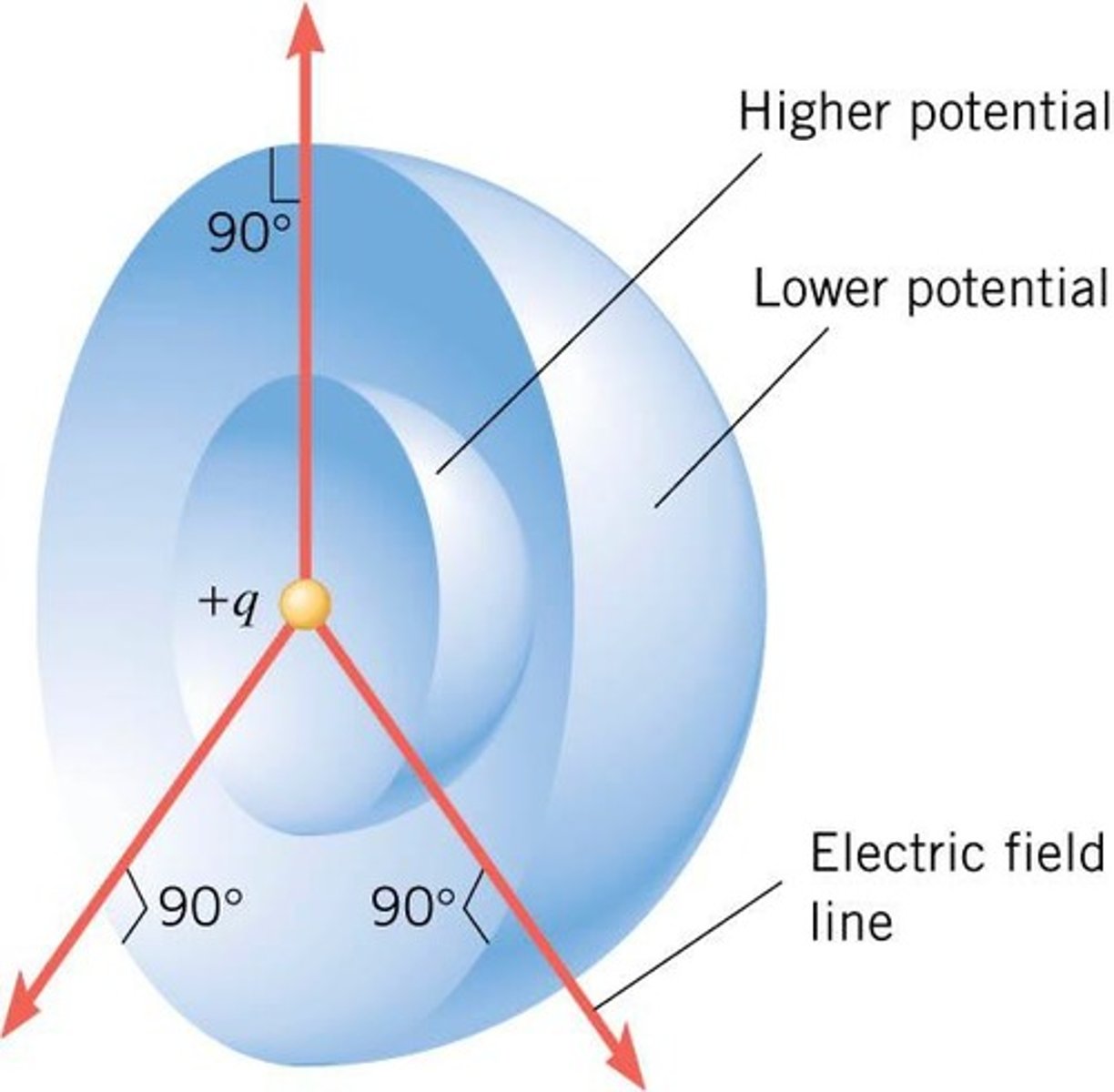
Equipotential Surfaces
Surfaces where electric potential is constant throughout.
Perpendicular Electric Field
Electric field lines are perpendicular to equipotential surfaces.
Potential Energy Change
Difference in potential energy between two positions.
Superposition Principle
Total potential is the sum of potentials from individual charges.
Point Charge Potential
Electric potential due to a single point charge.
Potential Energy Formula
U = kq1q2/r for two point charges.
Electric Potential Due to Multiple Charges
V = k * Σ(q/r) for N charges.
Equipotential Surface Properties
Electric field strength varies with spacing of surfaces.
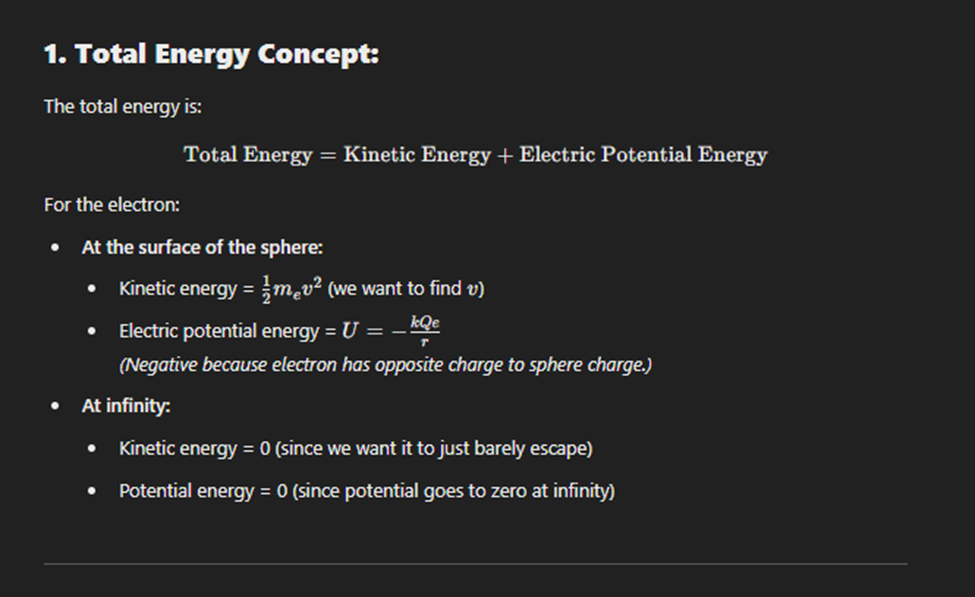
Potential Energy at Infinity
Potential energy considered zero at infinite separation.
Kinetic Energy at Infinity
Energy of a charge when moved far from others.
Potential Energy Calculation
U = kq1q2/r for two charges at distance r.
Electric Potential Gradient
Rate of change of electric potential with distance.
Work-Energy Theorem
Work done equals change in kinetic energy.
Distance (R) from Charge
Distance from a point charge affecting potential.
Charge (q)
Amount of electric charge influencing electric potential.
Coulomb's Constant (k)
Proportionality constant in electric force and potential equations.
Potential Energy Relative to Infinity
Energy comparison to a reference point at infinity.
Electric Field Line Direction
Direction where electric potential decreases.
Potential Energy of Charge System
Total energy of a system of interacting charges.
Electric Potential (V)
Work done per unit charge in an electric field.
Electric Potential Energy (U)
Work required to assemble a system of charges.
Point Charge
A charge located at a single point in space.
Continuous Charge Distribution
Charge spread over a region rather than concentrated.
Line Charge Density (λ)
Charge per unit length along a line of charge.
Surface Charge Density (σ)
Charge per unit area on a surface.
Electric Potential due to Point Charge
V = k(q/r) for a point charge.
Electric Potential due to Line Charge
Integrate contributions from all segments of charge.
Electric Potential due to Charged Ring
Potential from a ring treated as point charges.
Electric Potential Energy Formula
U = k(q_i * q_j/r_ij) for two charges.
Work Done by Electric Field
Work done moving a charge in an electric field.
Equipotential Surface
Surface where electric potential is constant.
Electric Field from Electric Potential
E = -∂V/∂s relates field to potential gradient.
Spherical Conductor Potential (r
V = (q/(4πε₀R)) for r inside conductor.
Spherical Conductor Electric Field (r
E = 0 inside a charged spherical conductor.
Spherical Conductor Potential (r>R)
V = (q/(4πε₀r)) for r outside conductor.
Spherical Conductor Electric Field (r>R)
E = (q/(4πε₀r²)) outside a charged conductor.
Total Electric Potential (V)
Algebraic sum of potentials from all charges.
Electric Potential Energy of System
U = Σ(k(q_i * q_j/r_ij)) for multiple charges.
Potential of Infinite Line Charge
V approaches infinity due to continuous charge.
Potential of Charged Disk
V calculated by integrating contributions from rings.
Potential Energy of Three Charges
U calculated for specific charge configurations.
Electric Potential Energy Work
Work done assembling charges from infinity.
Electric Potential Gradient
Rate of change of potential with distance.
Electric Field Components
E_x = -∂V/∂x, E_y = -∂V/∂y, E_z = -∂V/∂z.
Electric Potential at Center of Sphere
Potential is uniform and equals V = (Q/(4πε₀R)).
Work energy theorrme
Reference point at infinty (V =0, at inifity)
Electric potential
Change electric Potential energy
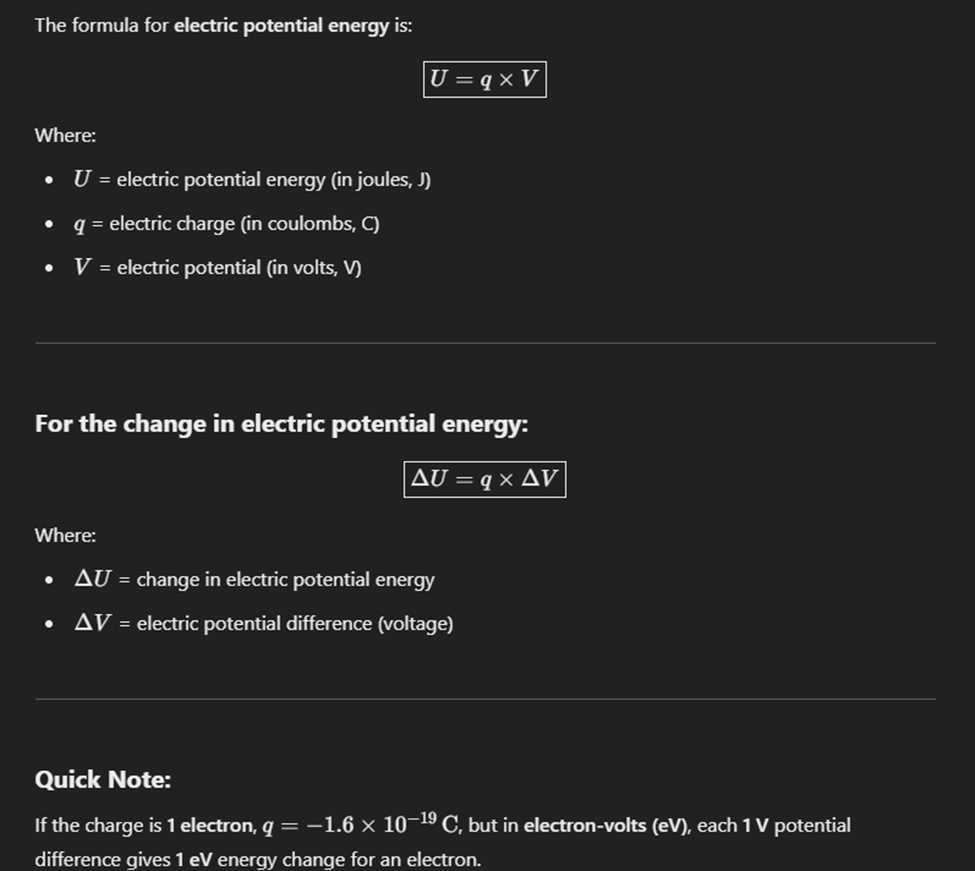
Work done
Electric field infinity sheet
the top is conducitivy 1/mohlm
Electric potential uniform electric field
Electric Potntial general field
Electric potetnital wiht dereviative
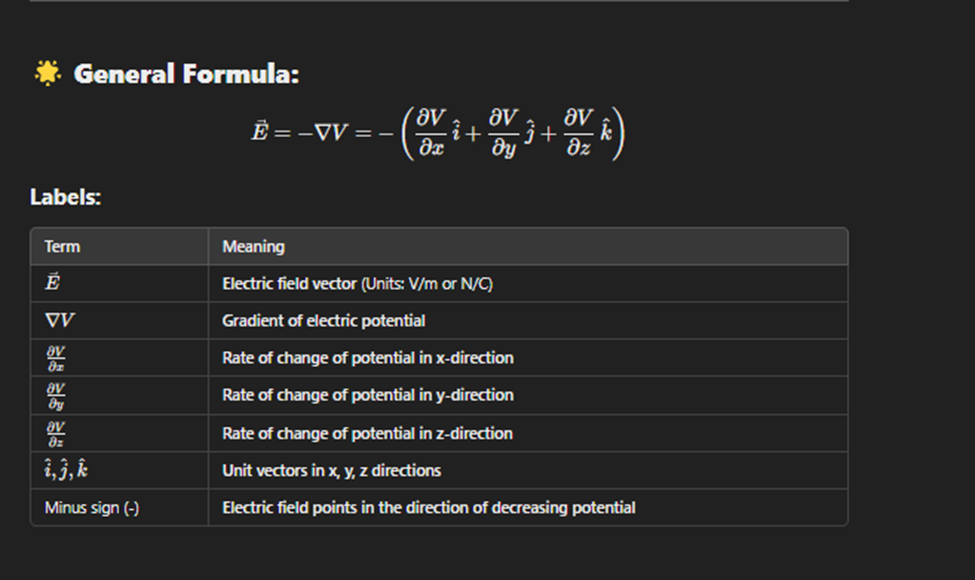
Electric force
Electric charge differential formula
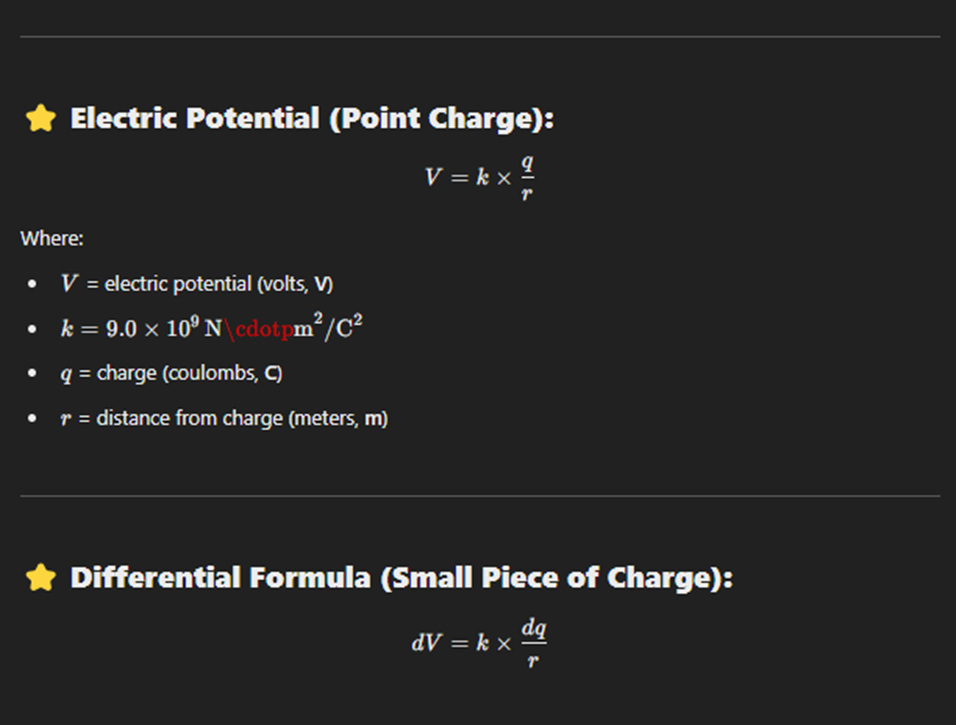
dq = linear density * dl
Potential group point charges
Electric potential infinite plane of charge
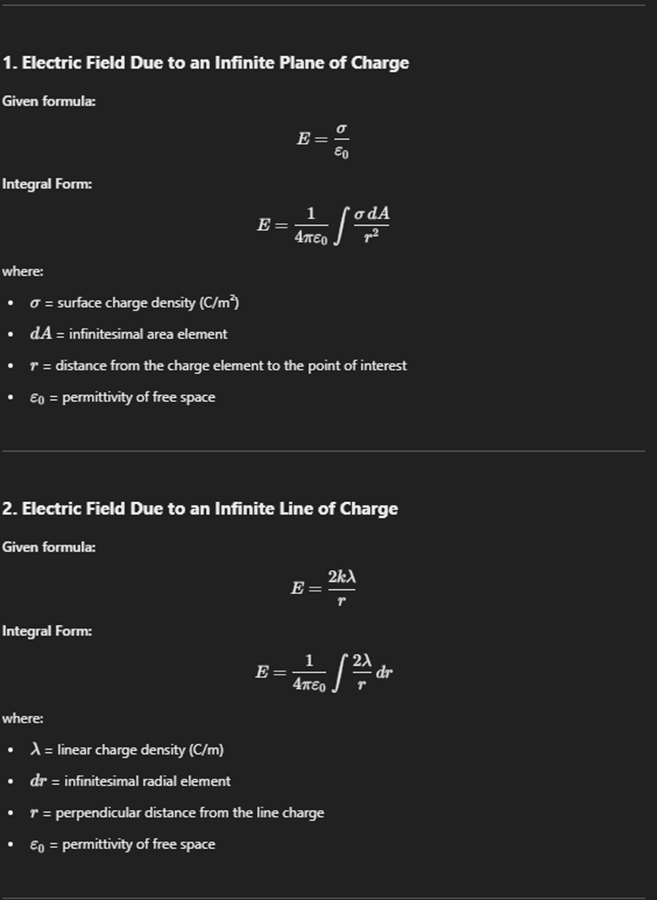
Electric potential enrgu (U)
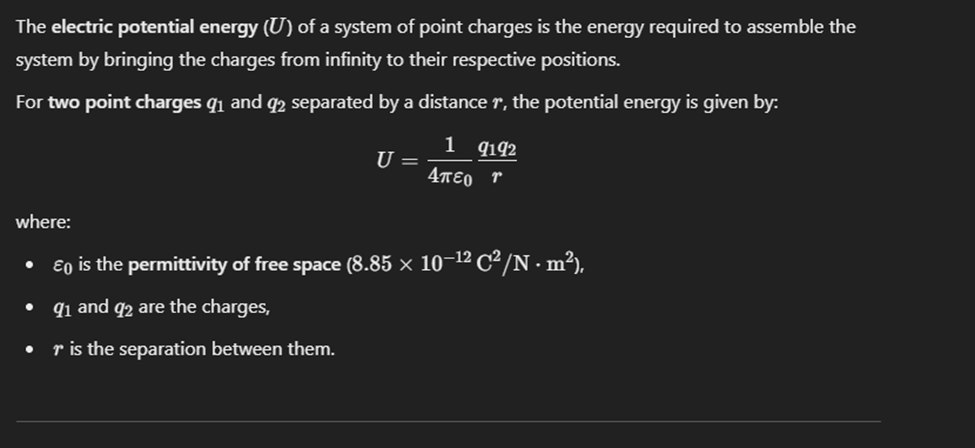
Electric potentail with capital Q
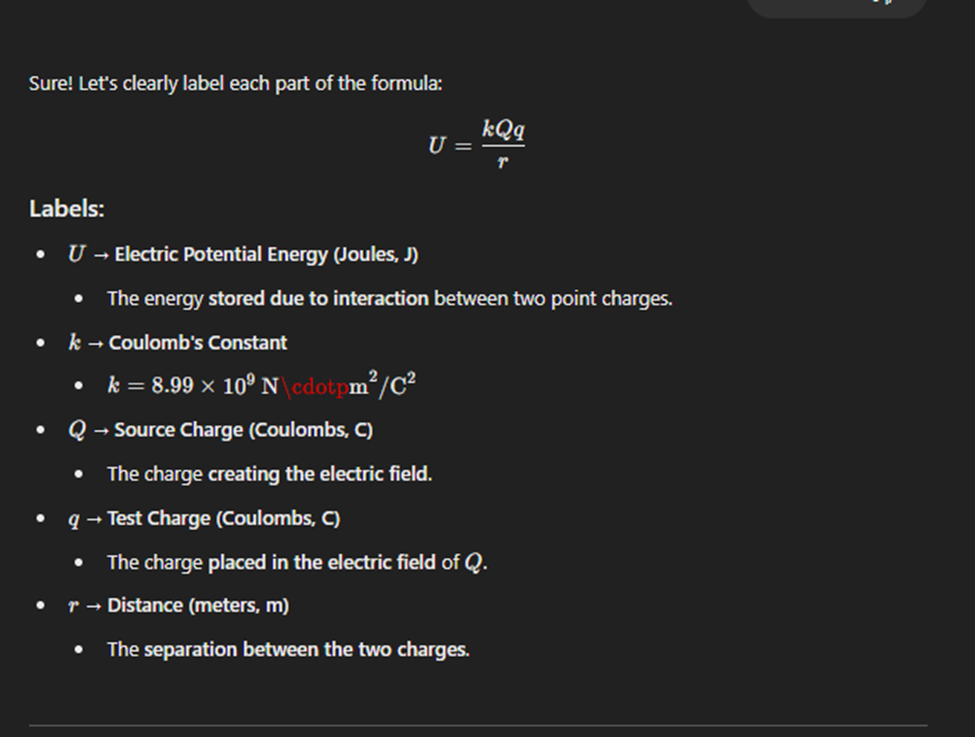
· Typically q will be charge of election and Q will be the charge of like what is given creating the electric field
Kinetic energy
