4.4 Theory of Computation

Define algorithm

- a sequence of steps that can be followed to complete a task, which always terminates (rather than going on forever in a loop)

Define abstraction

- the process of omitting unnecessary details from a problem

- used to simplify the problem and attempt to make finding a solution easier

Define representational abstraction

- a representation of a problem arrived at by removing unnecessary details from the problem

Define abstraction by generalisation/categorisation

- a grouping by common characteristics to arrive at a hierarchal relationship of the 'is a kind of' type

Define information hiding

- the process of hiding all the details of an object that don't contribute to its essential characteristics (e.g. using private variables)

Define procedural abstraction

- breaking down a complex model into a series of reusable procedures that can be used without needing to know the details of how the task is implemented

Define functional abstraction

- the process of breaking down a problem into smaller parts by defining functions that focus on what a task does rather than how the task is performed

- separated the purpose of a function from the details of its implementation; NOT INTEREST IN HOW THE FUNCTION DOES WHAT IT DOES, JUST THE RESULT

Define data abstraction

- when specific details of how data is actually represented is abstracted away, allowing new kinds of data structures to be created from previously defined data structures

(- think of abstract data structures e.g. queues, stacks)

What is problem abstraction/reduction?

- removing details from a problem until it is represented in a way that is solvable, generally by reshaping the problem into another form which has already been solved

Define decomposition

- diving a problem into a series of smaller sub-problems, each of which can be solved individually or further divided until all parts of the original problem have/can be solved

Define procedural decomposition

- the process of breaking down a problem into smaller subproblems each of which solve one identifiable problem and can be handled as a separate procedure/function

- these problems are then organised hierarchically and can be further subdivided

Define intractable problem and give two examples

- a problem which can be solved BUT

- for which no efficient solution belonging to polynomial time or below exists

- e.g. TSP, halting problem

Define heuristic

- a problem-solving strategy that uses practical, experience-based techniques or rules of thumb to find a good enough solution when finding the optimal or exact solution is too difficult, time-consuming or computationally expensive

(e.g. nearest neighbour UB for TSP, A* geographical heuristic for pathfinding)

Advantages of using heuristics

- faster (less computationally expensive) and simpler than exact algorithms

- provides workable solutions for complex problems

- can be used on large sets of data as the heuristic is a rule of thumb applied to every member, allowing for intercomparison of outputs

Disadvantages of using heuristics

- doesn't find the optimal solution and hence does not solve the problem

- results are volatile to slight optimisations in the heuristic which could change outputs wildly

What is compostion?

- the process of combining procedures to form a larger system e.g. in abstract data types which are formed from simple arrays

Define automation

- the process of putting abstractions of real-world phenomena (referred to as models) into action to solve problems

- achieved by implementing an algorithm in code, implementing models in data structures and finally executing the code on said structures

Describe the Halting problem. Why is it significant?

the problem: it is impossible to write an algorithm to determine if another algorithm will finish with a given input, and without running the other algorithm

significance: proves that there exist some problems which cannot be solved by computers

What is a universal Turing machine?

- a Turing machine that can simulate the behaviour of any other Turing machine and can compute any computable problem as they have infinite tape (memory)

Which concept do universal Turing machines exemplify and hence what can we stipulate they act as?

- they are an example of the stored program concept

- and therefore they can be said to act as interpreters because instructions are read in sequence before executing operations on their input data

Why are Turing machines significant?

- they provide a formal model of computation and therefore definition of what is computable

- they prove that there are problems that cannot be solved by computers as if a universal Turing machine can't do it, no computer can

Limitation of regular Turing machines

- they are limited to following just one FSM, making them specific to the one problem they are designed to solve

Define set

- a mutable abstract data type which stores an unordered collection of unique items and can contain other sets

Example set comprehension for positive integers

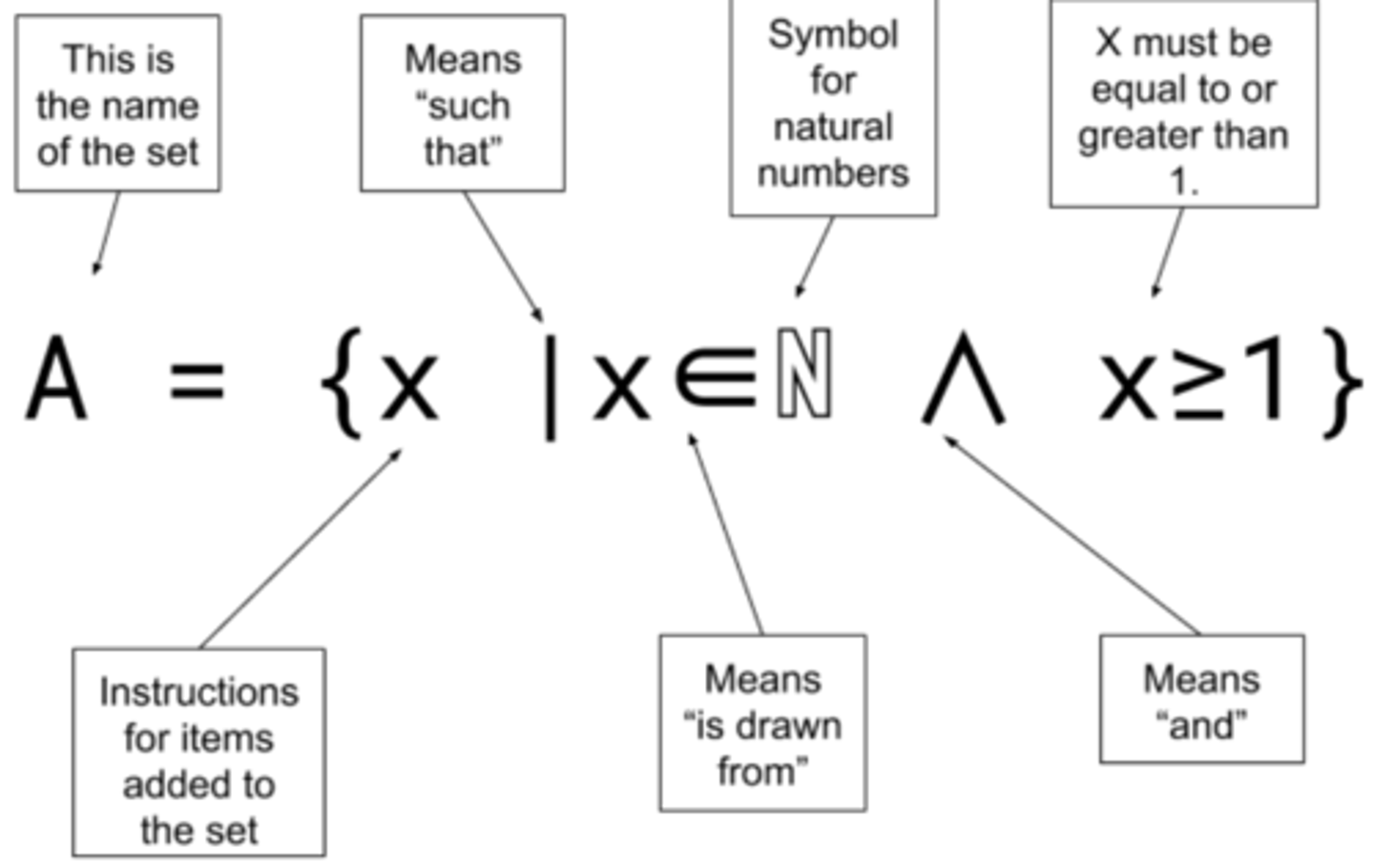
Define the set of the first 10 square numbers

S = {x*x | x ∈ N ^ x <= 10 }

Symbols for empty sets

What is the cardinality of a (finite) set?

- the number of elements in the set

What is a countably infinite set?

- a set in which each element can be paired to a natural number (but it just keeps on going)

- e.g. multiples of 3 are countably infinite: (1, 3), (2, 6), (3, 9) etc.

Example of a non-countable infinite set

- real numbers

What is a subset?

- given two sets, A and B, we say A is a subset of B if all elements of A are also elements of B (and A can be the same set as B)

- written as A ⊆ B

- NOTE: subsets do not need to have less members than the original set; the even numbers are a subset of the natural numbers but both are countably infinite

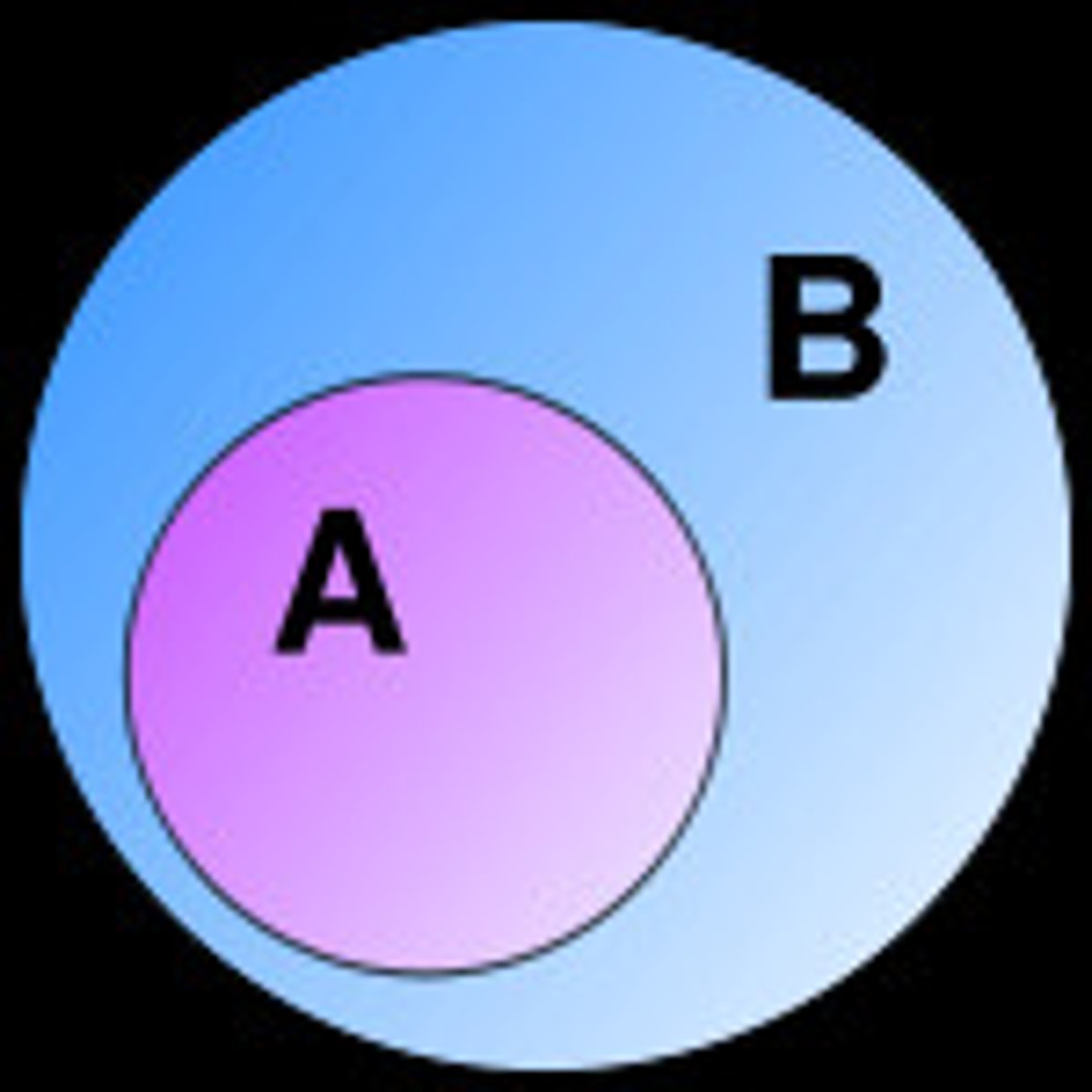
What is a proper subset?

- given two sets A and B, A is a proper subset of B if all the elements of A are in B, but A does NOT contain every element in B (they are NEVER the same set)

What does the difference operation do on a set?

- operator: \ or -

- if we take A\B or A-B, we get the set of elements unique to A (elements in A that are not in B)

Regular expressions metacharacters and meanings

*: 0 or more instances

+: 1 or more instances

?: 0 or 1 instances

| : or

() : grouping expressions

Is there an equivalent FSM for each set denoted by a regular expression?

YES

Is the set of string defined by a regular language always finite?

NO

Are there languages that can be represented in BNF that are not regular? Why?

YES

- BNF supports recursion and nesting which cannot be shown in regular expressions

Define context-free language

- a set of strings and symbols that follow the rules of a context-free grammar

(- context-free grammars describe which strings are and are not possible by laying out production rules)

example of context-free grammar: a -> ab (a can be replaced by ab)

Example of BNF recursion

- an integer is defined as a digit or a digit followed by an integer

- think like this: at each step we can add the last digit, or add a digit and call again to add another. when we add the last digit our integer is formed

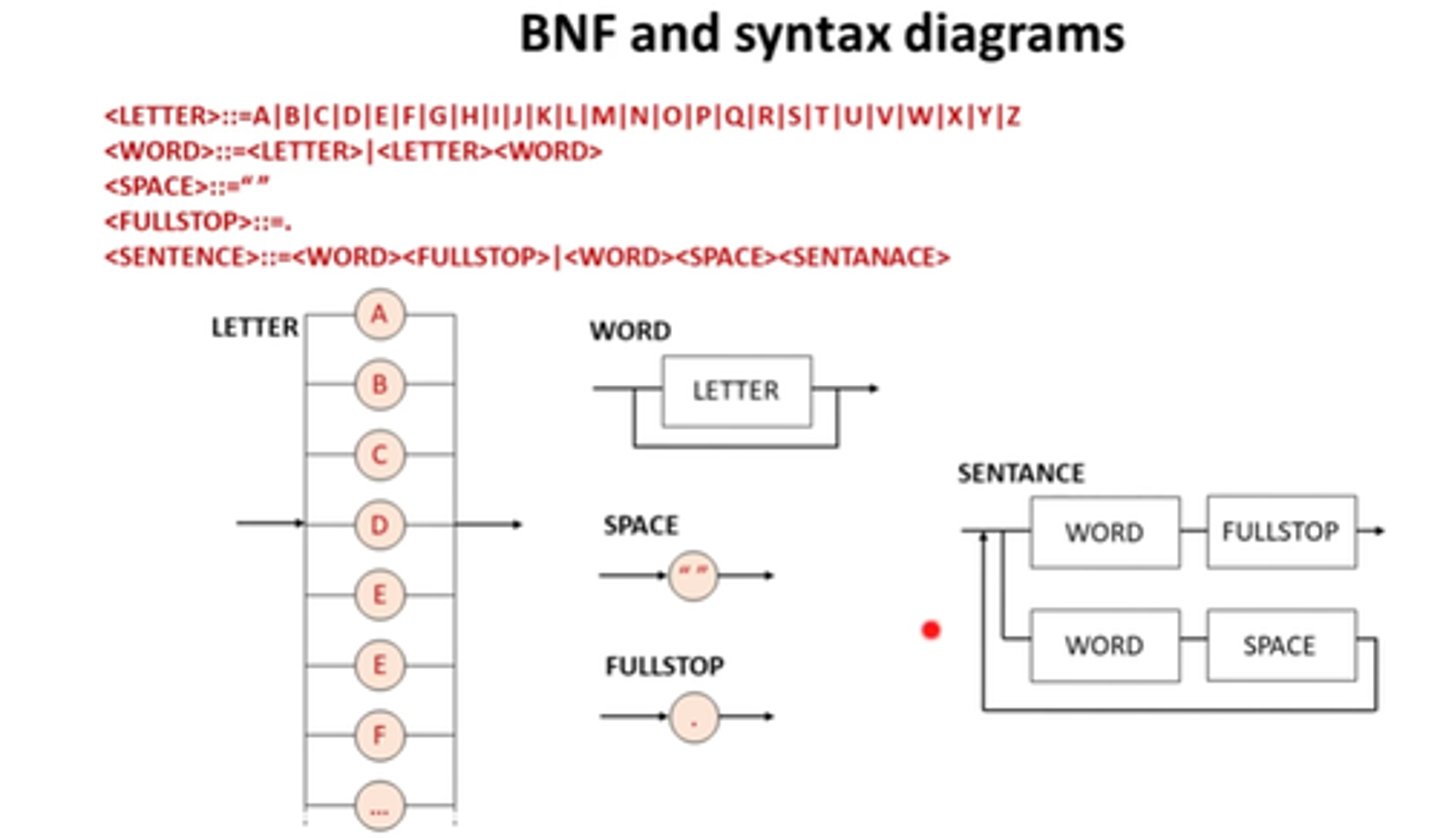
Explain syntax diagrams for BNF

- rectangles represent non-terminals i.e. BNF that can be broken down into more non-terminals, terminals or a combination e.g. ::= |

- ellipses represent terminals, which can't be broken down and must take a written value e.g. ::= 0|1|2...|9

Are there languages represented in regex that cannot be represented in BNF?

NO

- Regular languages are a subset of context free languages