271 Bus Stats - Ch2-3 - Examining relationships I-II & Producing data (Lec 4-5)

What to look for in a scatter plot ?

• direction of association

• strength of relationship

• outliers

What is the coefficient of correlation ?

°measures the strength of the linear association btwn 2 variables x&y.

= r

How to interpret the coef of variation ?

r is always btwn -1 & +1

• r>0 —> positive correlation

• r~=0 —> no correlation

• r<0 —> negative correlation

.r does not depend on the choice of explanatory / response variable

.r is only useful for linear relationships

Properties of coefficient of correlation ?

The closer to -/+1, the stronger the relationship

r does not depend on the units of measurement

Warning about coef of correlation ?

Outliers can influence correlation tremendously

What is the goal of linear regression ?

Make predications about how x (the explanatory or indpt variable) affects y (the response or dpt variable)

What tell us correlation ?

Correlation tells us about strength and direction of the linear relationship

A line is defined by ?

• the slope

• the intercept

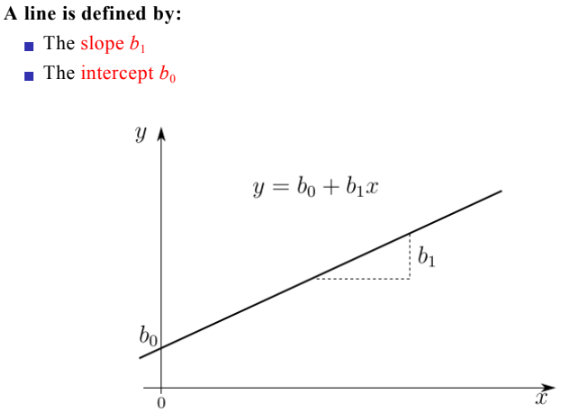
Define the line of best fit ?

°or least-squares line

The line that best fits y=b₀+b₁x has :

• slope b₁ = r(s_y/s_x)

• intercept b₀ = y^_ - b₁x^_

r = coef of correlation

sx = sample standard deviation of x1,…xn

sy = sample standard deviation of y1,…yn

x_ = sample mean of x1,…xn

y_ = sample mean of y1,…yn

Do the expl slide 33 Lec 4

— — LECTURE 5 — —

What are the 5 steps of linear regression ?

1. Choose a method for comparing lines (MSE is widely used)

2. Find the best line

3. Interpret the result

4. Evaluate the best line (how good is the line?)

5. Evaluate if linear regression is appropriate at all (residual analysis)

Step 1 : Compare lines

What criterion should we use to evaluate how ‘good’ a line is ?

The residual error (given a line ŷ = b₀ + b₁x) :

• error = observed value y - predicted value ŷ

• error_i = yi - (b₀ + b₁x_i)

The best (or “least-squares”) minimize the sum of squares of the residual errors :

• SOMMEⁿ_i=1(yi - (b₀ + b₁x_i))²

Step 2 : Find the best line

Compute ŷ

Observe that : … ?

What can we observe about ŷ ?

Observe that :

• the slop has the same sign as the correlation coef r

• if the variables x&y are reversed, r stays the same, but the slope & intercept will change

• The best best fit line always … ?

The best best fit line always … ?

The best best fit line always passes through the point (x^_,y^_)

Step 3 : Interpret the results

Do the expl Slides 18-21 Lec 5

Step 4 : How good is the best line ?

Measure the “Goodness of Fit” :

• the coef of determination : =r²

• represents the fraction of the variation in y that is explained by changes in x

  • So r is a p%, of how much of the variation in y can be explained by changes in x

• Since -1 <= r <= 1, we always have 0 <= r² <= 1

Should we always use linear regression ?

To see if it makes sense to use linear regression, we make a residual plot

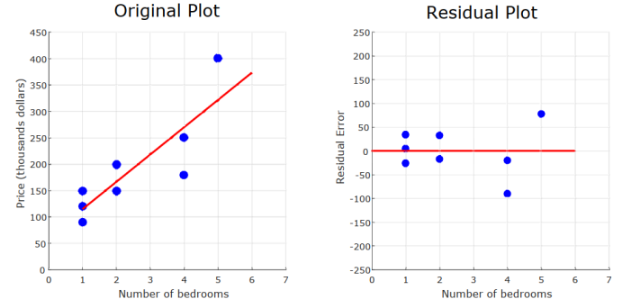
Step 5 : Residual Analysis

Draw residual plot

Residual plot ?

°a plot where the x-values are the same as in the scatter plot, but the y-values are the residual errors

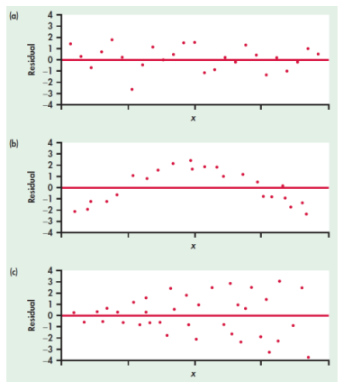
What observation can we make about residual plots ?

1. No pattern : Residuals are randomly scattered

   • Ccl : Linear regression is good!

     = Homoskedasticity

2. Pattern : Residuals show surved pattern

   • Ccl : Nonlinear relationship: Linear regression is not good

3. No pattern But a change in variability

   • Ccl : we can use linear regression, but predictions will not be as good when variability is larger

     = Heteroskedasticity (lvl of vairaiton is variable, volatility is volatile)

Cautions about correlation and regression ?

• Always look for the scatter plot and do not trust blindly the value of r! A single outlier or observation that is far from the other data points can have a major effect on the value of r, and on the regression line.

  • significantly weaker (less negative, more positive), when outlier (large residual error)

  • significantly stronger (more negatiev, positive), new point far but not especially large residual error

• ! beware extrapolation ! : difficult to predict values of the explanatory variable far from the observed values

• Association ≠ Causation (not bc 2 variables go in the same direction that they are linked, it can be hazard)

— — Producing Data — — (Ch3)

Census vs sample ?

°Census : measures every ind in the pop

°Sample survey : measures only a subset of the pop

Observational vs experimental data ?

°Observational study : Record data on indvls without attempting to influence the responses

°Experiment : Impose a treatment on indvls and record responses.

Common sample designs ?

• Convenience sampling

• Voluntary response sampling

• Simple random sampling

• Stratified random sampling

• Convenience sampling?

• Voluntary response sampling?

• Simple random sampling?

• Stratified random sampling?

• Systematic sampling?

• Cluster sampling?

When is sample design biased ?

When it systematically favors certain outcomes

Common sources of bias ?

• Undercoverage

• Non-response

• Untruthful/inaccurate responses

• Wording of questions influences answers

Excel :

• Coef of correlation ?

• Step 1

• Step 4

• CORREL(var1, var2)

Do ex 1 & 2 Slides 47-48 Lec 5

• Suppose the standard deviation of y₁

  ,...,y_n is 20, and the standard deviation of x₁,...,x_n is 10.

  ==> What is the biggest possible value of the slope of the regression line?

• Suppose y^_=1.5, s_x=3, r=0.5, b₁=2, and b₀=1.

  1 What is the standard deviation of y?

  2 What is the mean of y?