Scalars and Vectors

Two types of quantities:

Scalars and vectors

Quantities that have magnitude but not direction

Scalars

The extent, size, or amount of something

Magnitude

Mass is a scalar/vector quantity

Scalar

Why is mass a scalar quantity?

It has magnitude but no direction

Quantities that have both magnitude and direction

Vectors

Weight is a scalar/vector quantity

Vector

Why is weight a vector quantity?

It is a force and has both magnitude and direction

A measure of how far an object has travelled, regardless of direction

Distance

The total length of the path taken

Distance

Does distance have magnitude?

Yes

Does distance have direction?

No

Distance is a scalar/vector quantity

Scalar

A measure of how far it is between two points in space, including the direction

Displacement

The length and direction of a straight line drawn from the starting point to the finishing point

Displacement

Does displacement have magnitude?

Yes

Does displacement have direction?

Yes

Displacement is a scalar/vector quantity

Vector

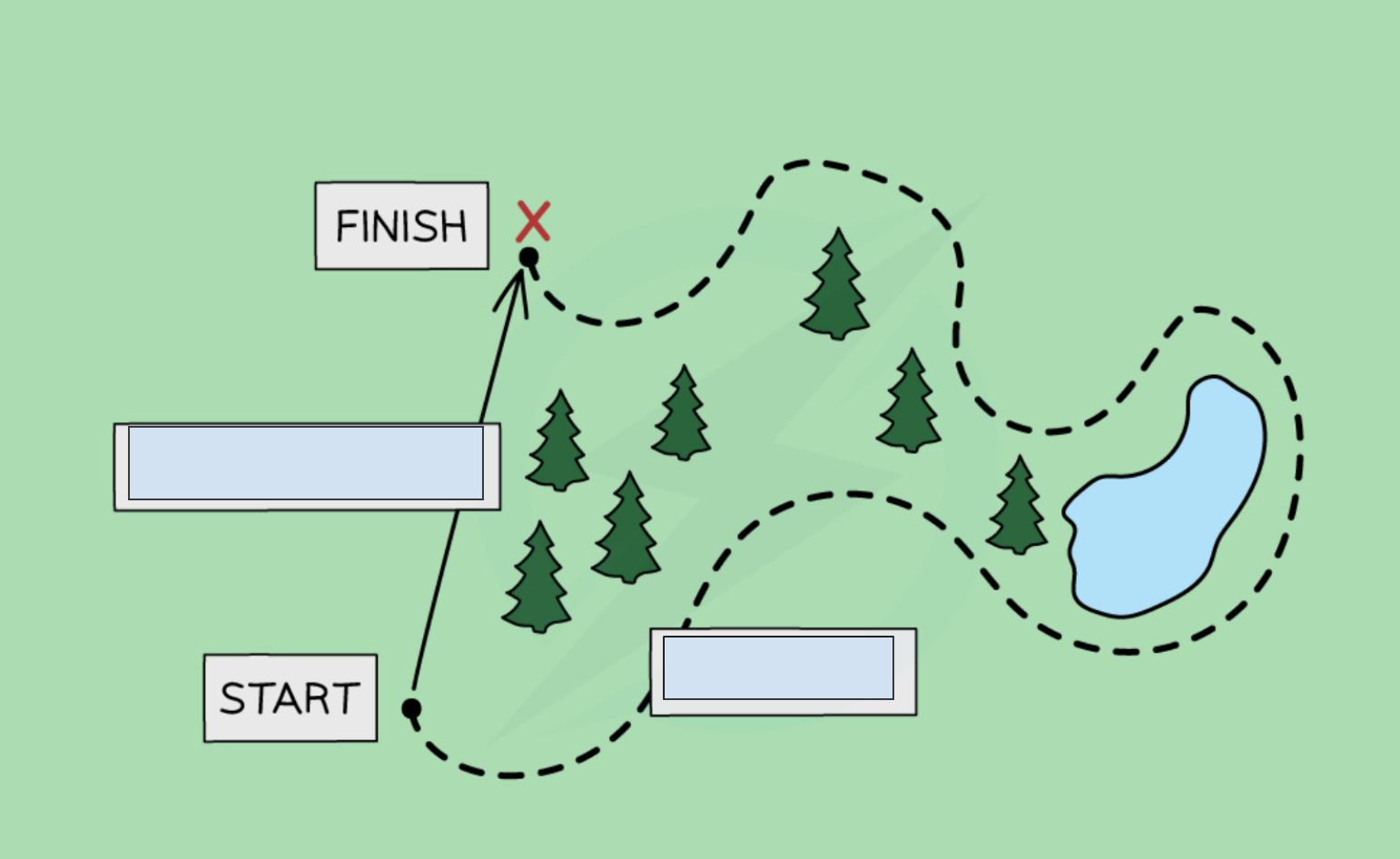
Which one is displacement and which is distance?

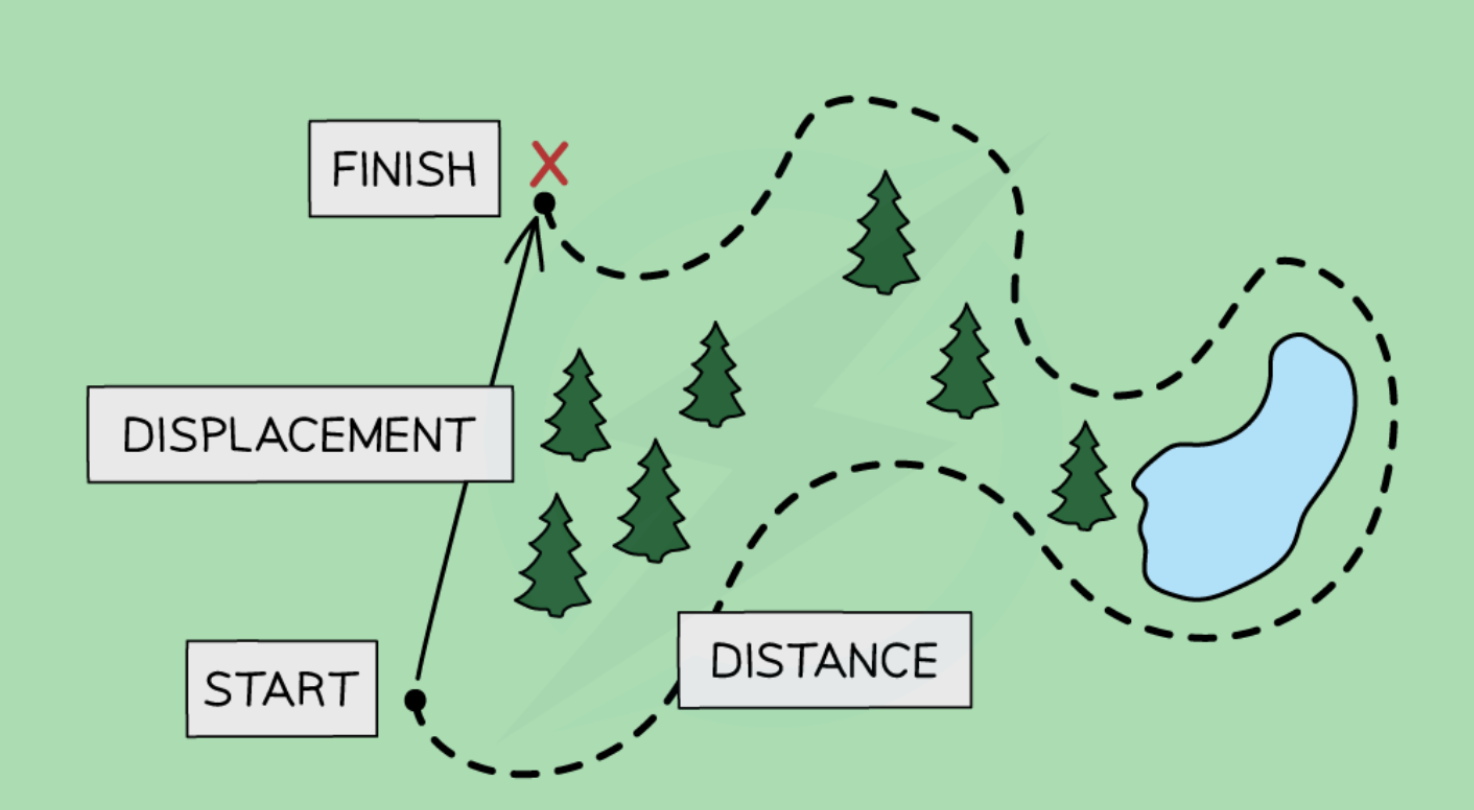
When a student travels to school, will there probably be a difference in the distance they travel and their displacement?

Yes

When a student travels to school, the overall distance they travel includes the:

Total lengths of all the roads, including any twists and turns

When a student travels to school, the overall displacement of the student would be a:

Straight line between their home and school

When a student travels to school, does the overall displacement take into account obstacles like buildings, lakes or motorways?

No

A measure of the distance travelled by an object per unit time, regardless of the direction

Speed

Speed of an object describes how:

Fast it is moving

Does speed of an object describe the direction it is traveling in?

No

Does speed have magnitude?

Yes

Does speed have direction?

No

Speed is a scalar/vector quantity

Scalar

A measure of the displacement of an object per unit time, including the direction

Velocity

The velocity of an object describes how:

Fast it is moving and which direction it is traveling in

Can an object have a constant speed but changing velocity?

Yes

When can an object have a constant speed but changing velocity?

If it is changing direction

Does velocity have a magnitude?

Yes

Does velocity have a direction?

Yes

Velocity is a vector/scalar quantity

Vector

Distance is a scalar/vector quantity

Scalar

Speed is a scalar/vector quantity

Scalar

Mass is a scalar/vector quantity

Scalar

Time is a scalar/vector quantity

Scalar

Energy is a scalar/vector quantity

Scalar

Volume is a scalar/vector quantity

Scalar

Density is a scalar/vector quantity

Scalar

Pressure is a scalar/vector quantity

Scalar

Electric charge is a scalar/vector quantity

Scalar

Temperature is a scalar/vector quantity

Scalar

Displacement is a scalar/vector quantity

Vector

Velocity is a scalar/vector quantity

Vector

Acceleration is a scalar/vector quantity

Vector

Force is a scalar/vector quantity

Vector

Momentum is a scalar/vector quantity

Vector

Vectors are represented by an:

Arrow

The arrowhead indicates the _______ of the vector

Direction

The length of the arrow represents the ______ of the vector

Magnitude

Vectors can be combined by:

Adding or subtracting them from each other

Two methods to combine vectors:

Triangle and parallelogram method

How to combine vectors with the triangle method?

Link the vectors head-to-tail

When using the triangle method, the resultant vector is formed by:

Connecting the tail of the first vector to the head of the second vector

How to subtract vectors using the triangle method?

Change the direction of the vector from positive to negative and add them in the same way as when adding vectors

The triangle method links vectors ___ to ___ to find the resultant vector

Tip, tail

How to combine vectors using the parallelogram method?

Link the vectors tail-to-tail and complete the resulting parallelogram

When using the parallelogram method, the resultant vector is the:

Diagonal of the parallelogram

The parallelogram method links vectors ___ to ___ to find the resultant vector 

Tail, tail

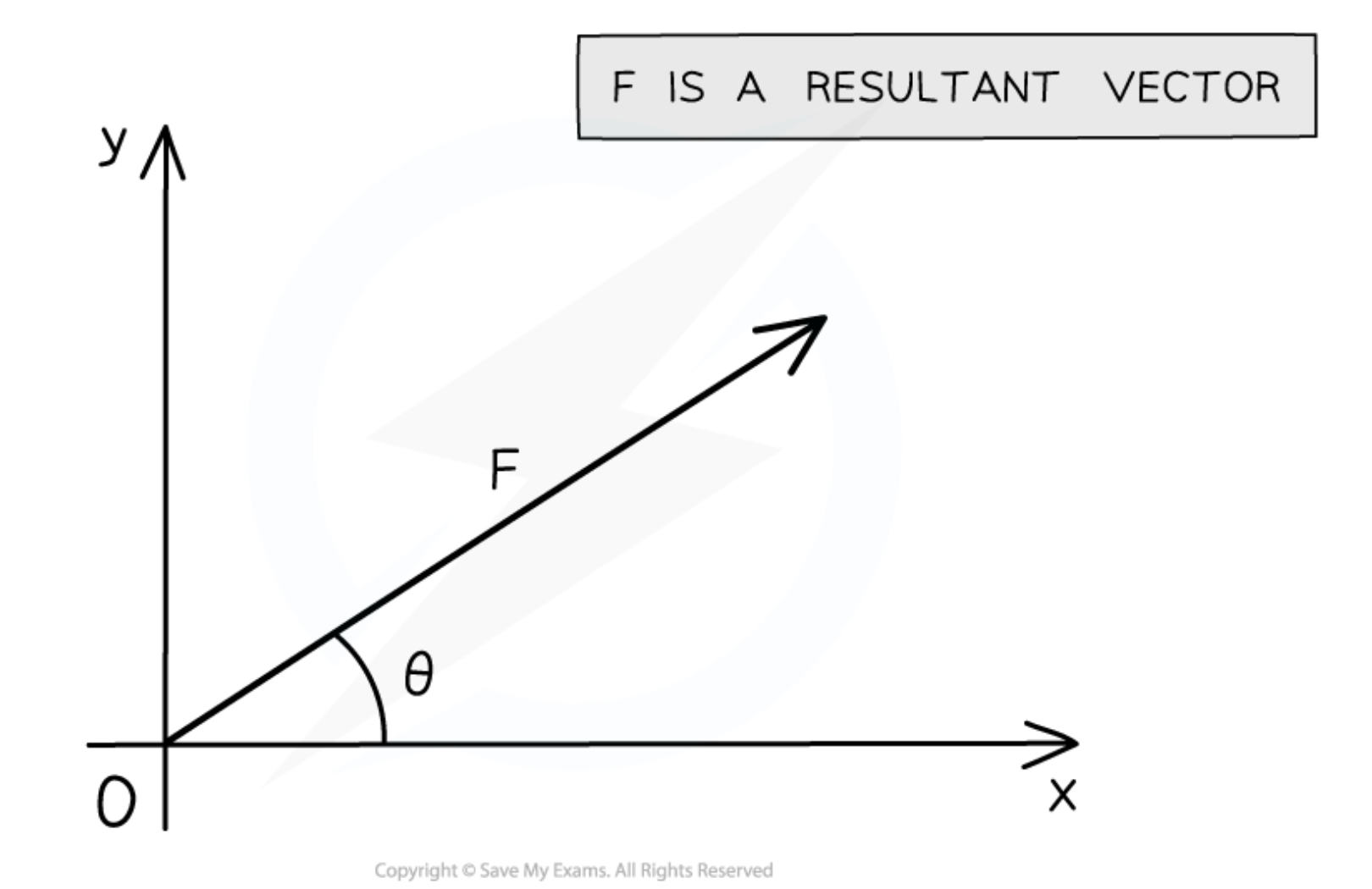
When two or more vectors are added together (or one is subtracted from the other) using the parallelogram method, a single vector is formed, known as the:

Resultant vector

When using the parallelogram method, the magnitude of the resultant vector can be found using:

Pythagoras' theorem or trigonometry

Forces which act in the same plane

Coplanar forces

Coplanar forces can be represented by:

Vector triangles

In equilibrium, vector triangles are:

Closed

When vectors are joined together, they form a:

Closed path

If three forces acting on an object are in equilibrium; they form a:

Closed triangle

Two vectors can be represented by a:

Single resultant vector

Does the single resultant vector that represents two vectors have the same effect as the original vectors?

Yes

How can a single resultant vector be resolved?

By being represented by 2 vectors

When a single resultant vector is represented by 2 vectors, the vectors in combination have the same ______ as the original one

Effect

When a single resultant vector is broken down into its parts, those parts are called:

Components

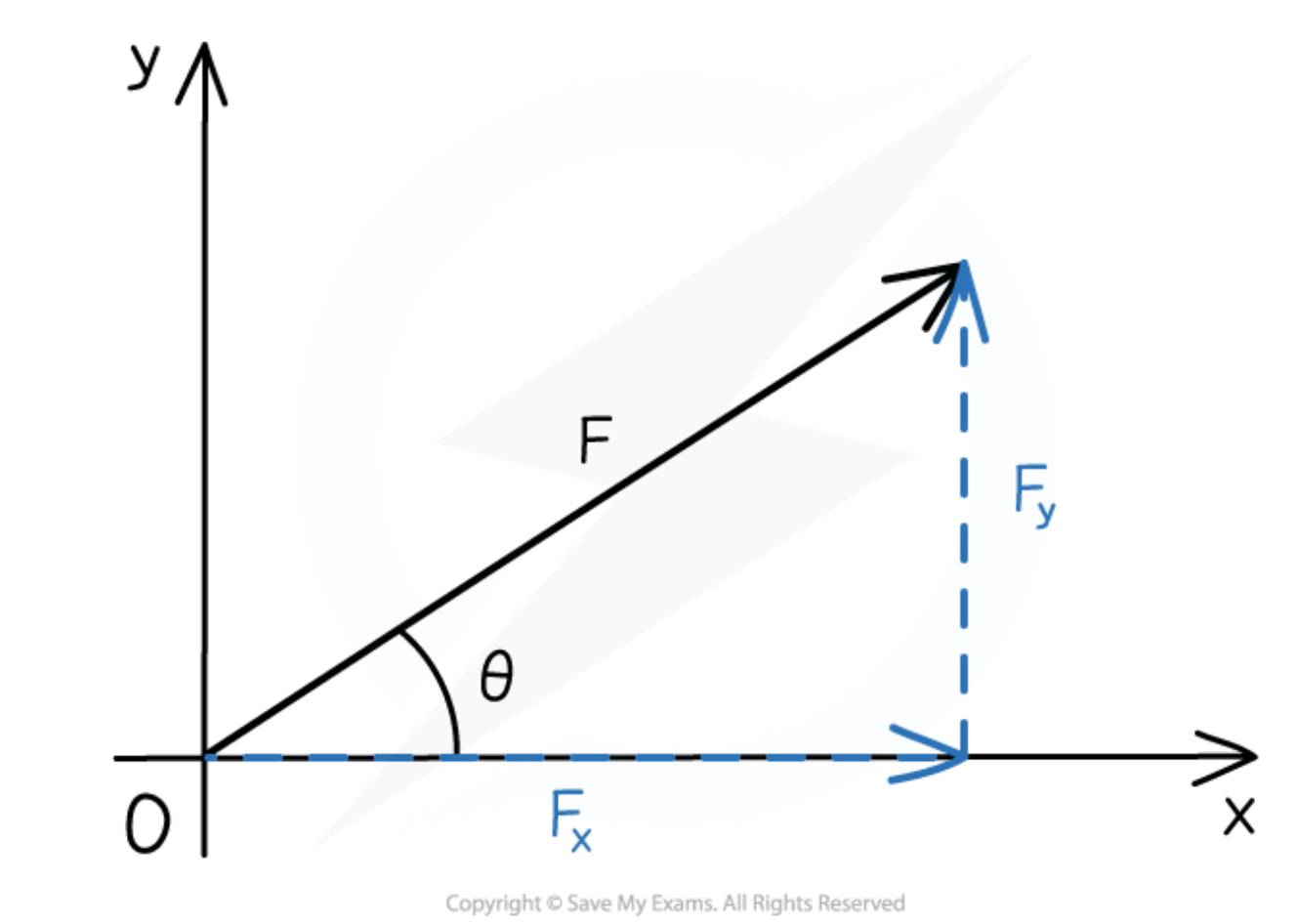
Is it possible to resolve this vector into its horizontal and vertical components?

Yes

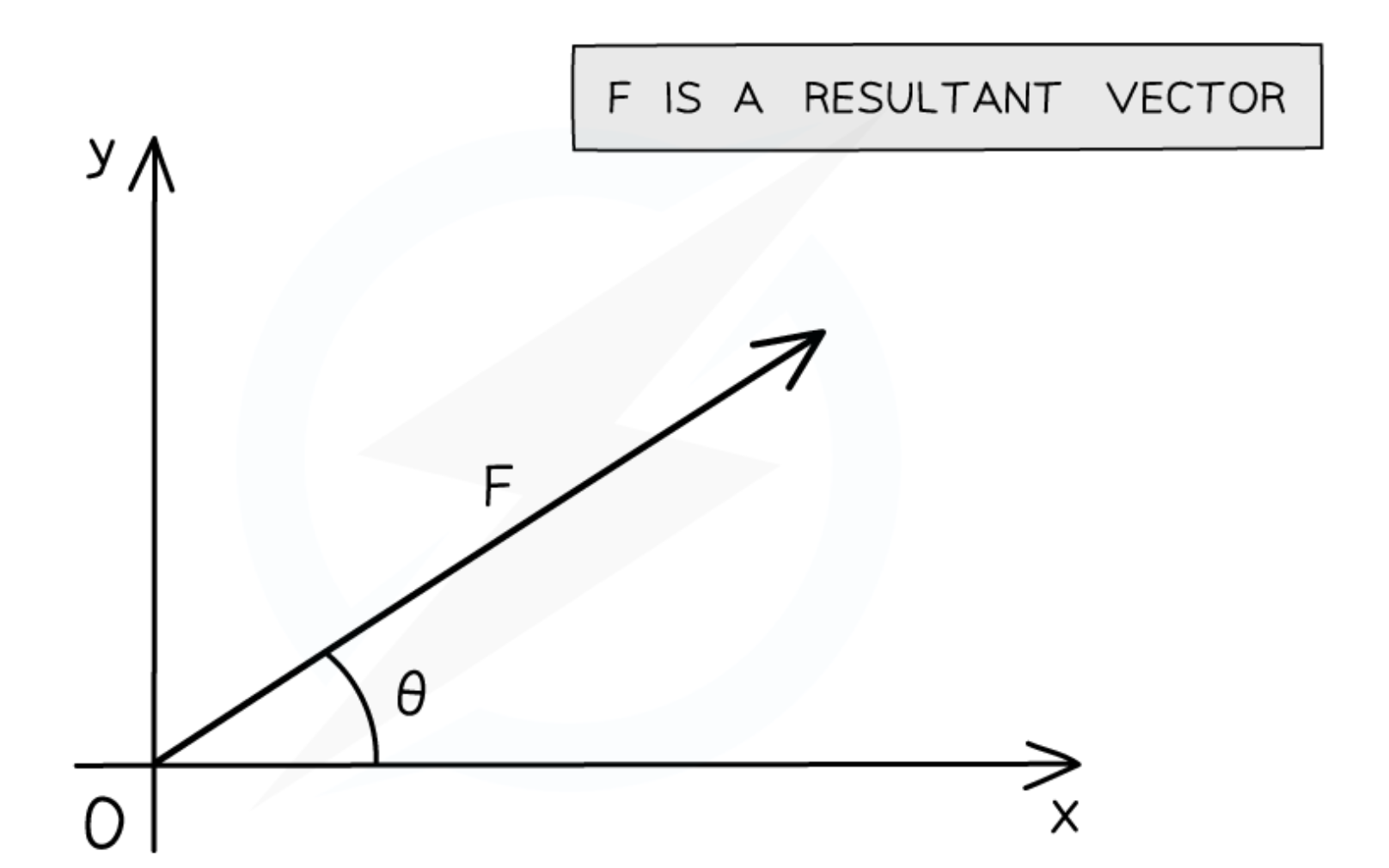
How to resolve this vector into its horizontal and vertical components?

By using trigonometry

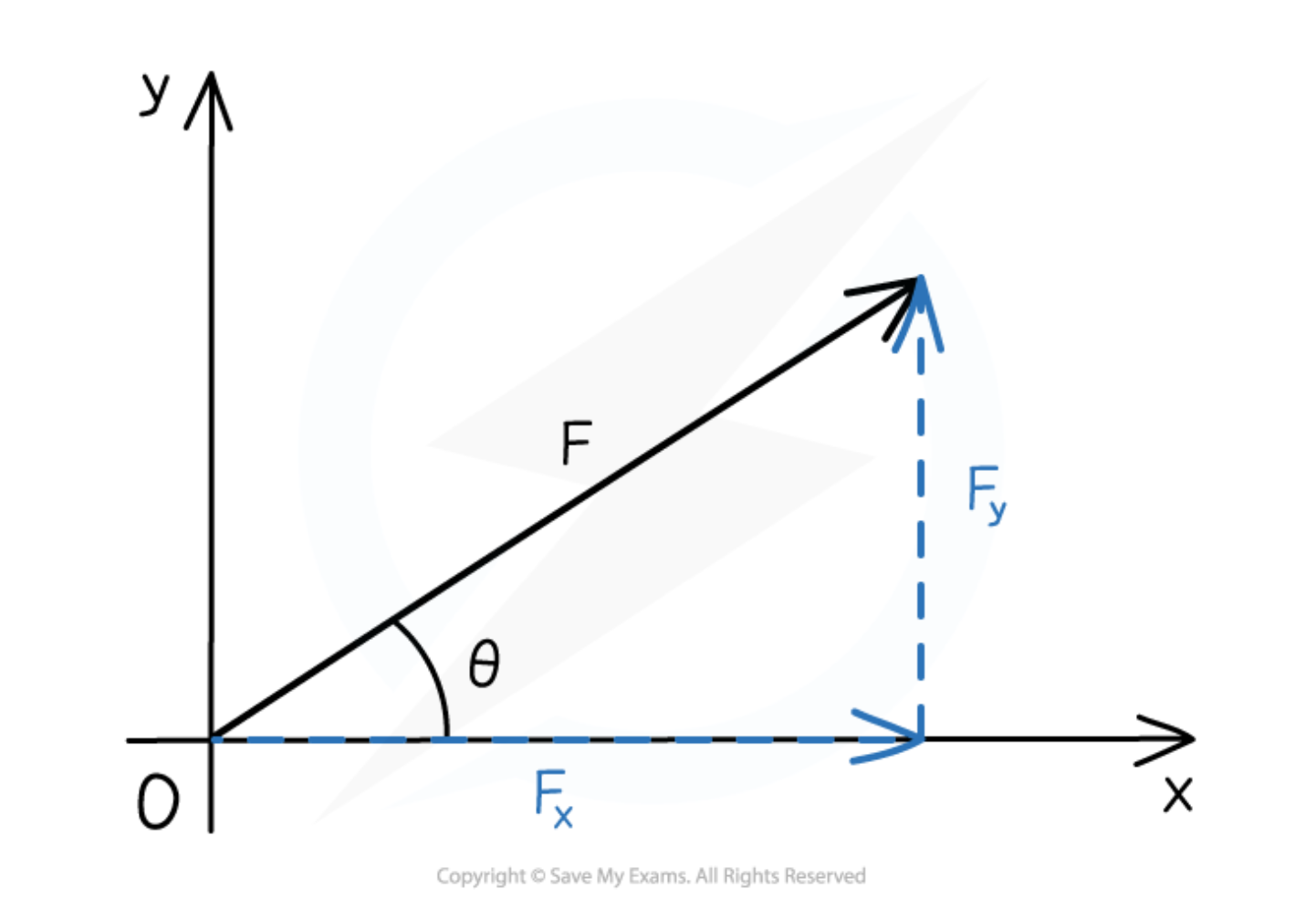
How to calculate Fx?

F_x = Fcosθ

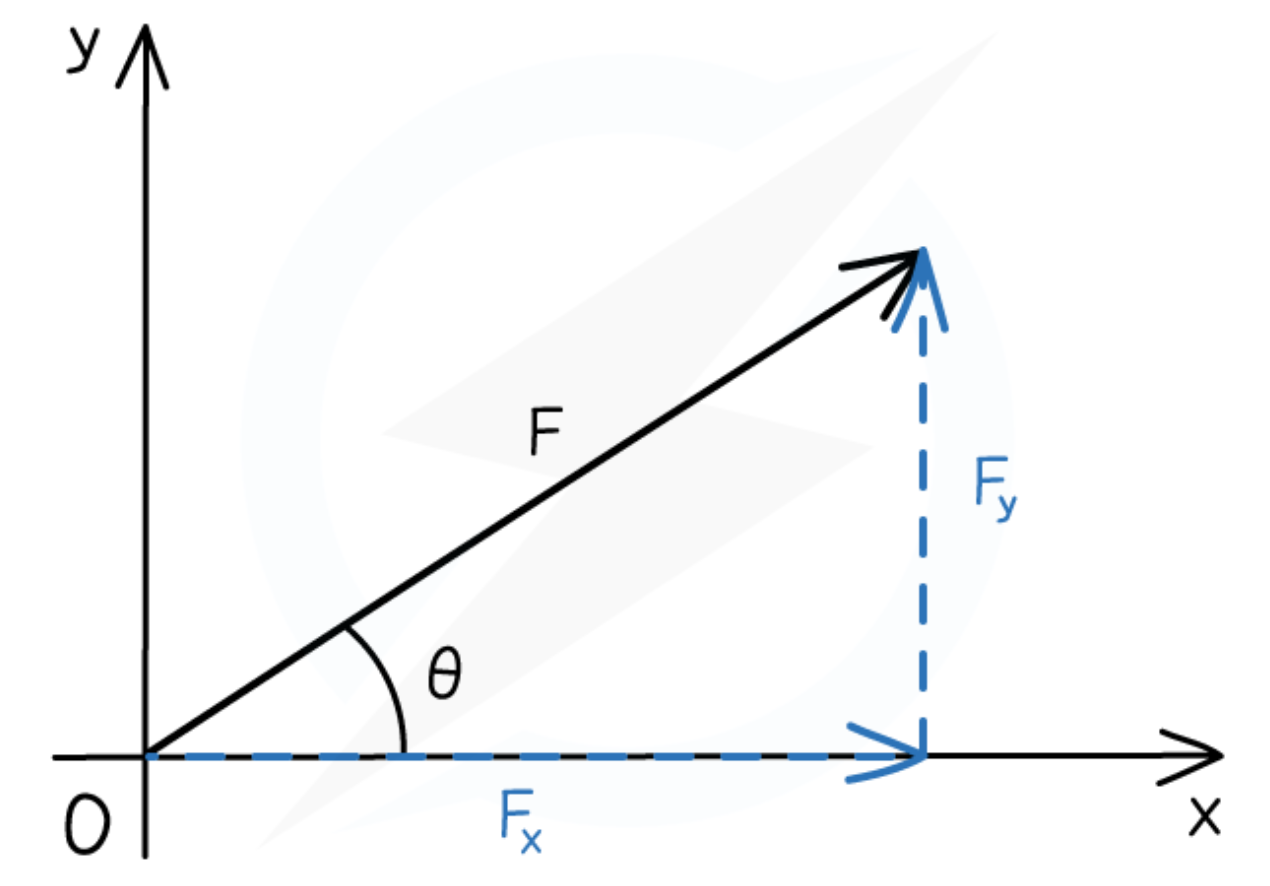
How to calculate Fy?

F_y = Fsinθ

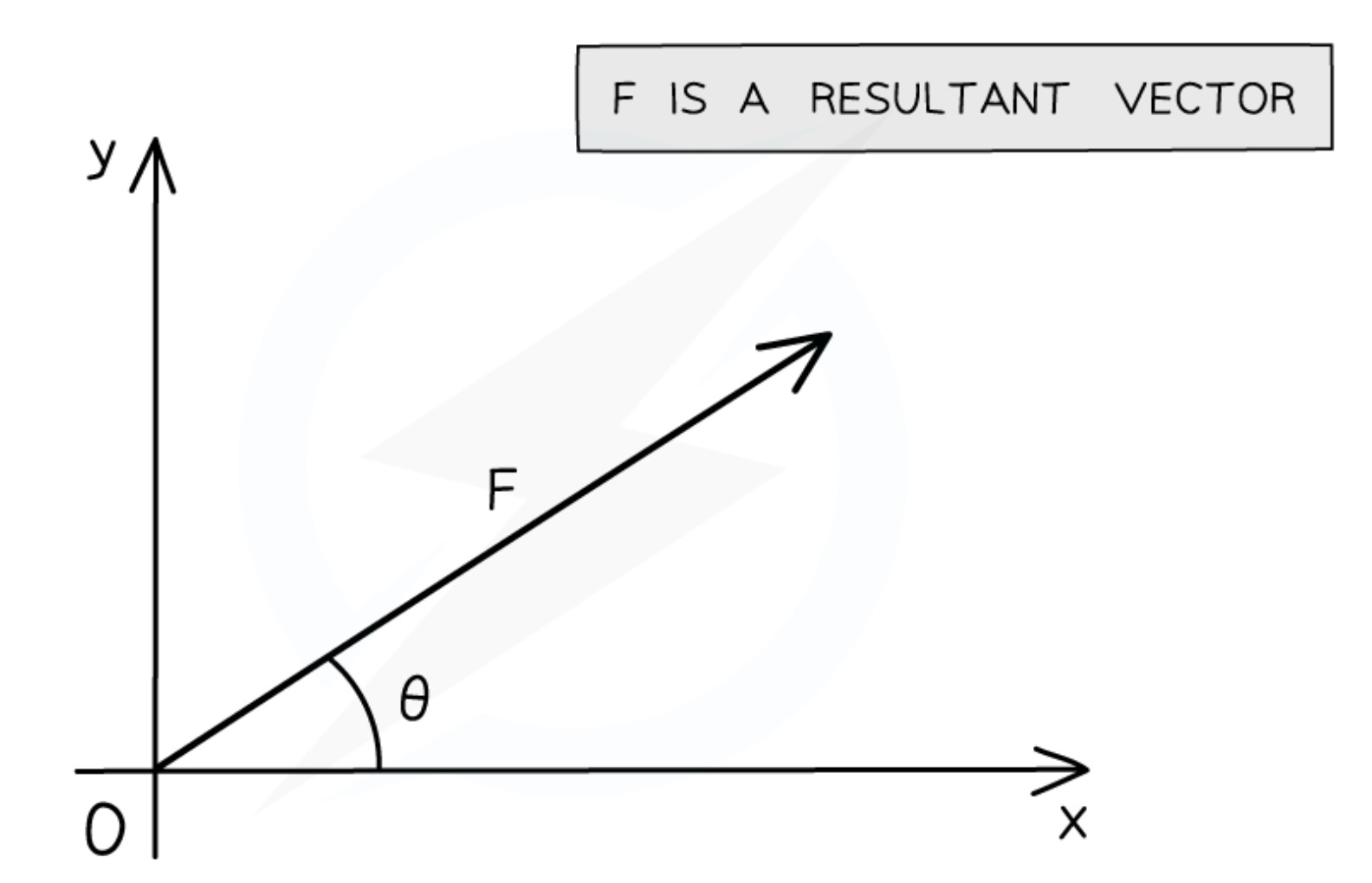
Draw the horizontal and vertical components of F: