Ramp Function (Part-II)

Discrete-Time Ramp Function

A signal that increases linearly with the discrete-time index for nonnegative values and is zero otherwise.

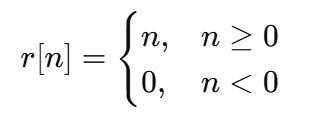
r[n] = n u[n]

• Ramp Function Relation to Unit Step (Discrete-Time)

• The discrete-time ramp function can be expressed as the product of the index and the unit-step function.

i(t) = I0u(t)

• Unit-Step Representation of a Switching Event

• A sudden change in a circuit (such as opening a switch at t=0t = 0t=0) can be modeled using the unit-step function.

Capacitor Voltage–Current Relationship

The voltage across a capacitor equals the time integral of its current scaled by the reciprocal of capacitance.

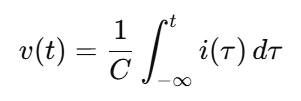
Ramp Response of a Capacitor to a Step Current

If a step current I0u(t) is applied to a capacitor, the resulting voltage is a ramp function.

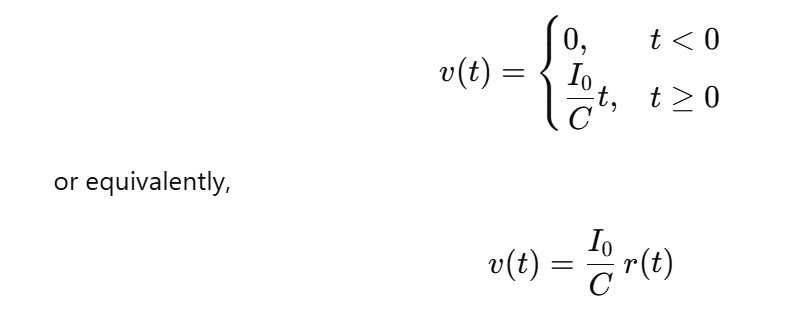
y(t) = H{x(t)}

• Continuous-Time System (Operator View)

• A system can be viewed as an operator H that maps an input signal to an output signal.

y[n] = H{x[n]}

• Discrete-Time System (Operator View)

• In discrete time, a system transforms an input sequence into an output sequence through an operator.

y[n] = (1/3)(x[n] + x[n - 1] + x[n - 2])

• Moving-Average System (3-Point)

• A discrete-time system whose output is the average of the three most recent input samples.

(S^k)x[n] = x[n - k]

• Time-Shift Operator

• An operator that delays a discrete-time signal by a fixed number of samples.

H = (1/3)(1 + S + S^2)

• Operator Representation of a Moving-Average System

• The moving-average system can be represented compactly using time-shift operators.

Cascade Implementation of a System

• A system implementation where signals pass sequentially through multiple subsystems.

• Example: cascading two unit-delay blocks S to obtain S²

Parallel Implementation of a System

• A system implementation where multiple signal paths operate simultaneously and are summed.

• Used to implement: H = (1/3)(1 + S + S²)

Feedback Connection

• A system configuration where part of the output is fed back to the input, forming a closed loop.

• Used to improve performance but may introduce stability concerns.

Linear Growth Signal

• A signal whose amplitude increases proportionally with time or index.

• Continuous-time: r(t) = t u(t)

• Discrete-time: r[n] = n u[n]

Physical Interpretation of a Ramp Signal

Represents constant-rate accumulation, such as:

• Capacitor voltage under constant current

• Angular displacement under constant rotational speed